Порождающие модели

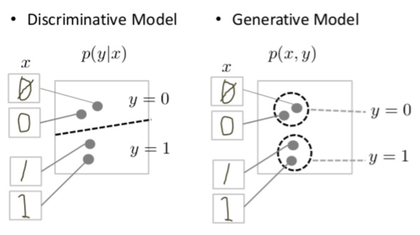
Порождающая модель пытается генерировать рукописные 0 и 1, для этого моделирует распределение по всему пространству данных. Напротив, дискриминативная модель старается разделить данные, без необходимости точно моделировать, как объекты размещаются по обе стороны от линии.

Порождающие модели (англ. generative model) — это класс моделей, которые обучают совместное распределение данных [math]p(x, y)[/math]; отсюда легко получить условное распределение [math]p(y \mid x)={p(x, y)\over p(x)}[/math], но совместное даёт больше информации и его можно использовать, например, для генерации новых фотографий животных, которые выглядят как настоящие животные.

С другой стороны, дискриминативная модель (англ. discriminative model) обучает только условное распределение и может, например, отличить собаку от кошки.

Классификация задачи

Можно использовать некоторые эмпирические правила для генерации новых объектов, не используя машинного обучения.

Мы хотим научиться создавать правдоподобный объект относительно некоторой скрытой структуры исходных объектов. Давайте изучим распределение по ним, а затем просто будем сэмплировать новый объект из этого распределения. Значит эта задача относится к классу задач обучения без учителя.

Порождающая модель иногда позволяет использовать обучение с частичным привлечением учителя. Пусть задача состоит в том, чтобы отличить кошек от собак на фотографиях. Обычно мало размеченных данных, на которых кошки и со­баки отмечены вручную. Основная часть задачи со­стоит в том, чтобы понять, чем разумные фотографии отличаются от слу­чайного шума. Иначе говоря, если сначала определить распределение [math]p(x)[/math], то проще обучить распределение [math]p(y \mid x)[/math], где [math]y[/math] — это один бит, отвечающий за отдельный признак, а [math]x[/math] — это вся фотография.

Вычисление плотности распределения

С математической точки зрения основная цель порождающей модели обычно состоит в максимизации функции правдоподобия: для набора данных [math]X = \{x_i\}[/math] максимизировать [math]\displaystyle \prod_i p_{model}(x_i;\theta)[/math] по параметрам модели [math]\theta[/math], т.е. найти [math]\theta^* = \underset{\theta}{\operatorname{argmax}} \displaystyle \prod_i p_{model}(x_i;\theta)[/math]

Чтобы избежать арифметического переполнения снизу зачастую пользуются свойством логарифма произведения [math]\log ab = \log a+\log b[/math]. Благодаря моннотоности логарифма, его применение к обоим частям выражения не изменит параметры, при которых достигается максимум. При этом, логарифм от числа близкого к нулю будет числом отрицательным, но в абсолютном значении существенно большим чем исходное число, что делает логарифмические значения вероятностей более удобными для анализа. Что в нашем случае с вероятности очень уместно. Поэтому, мы переписываем нашу формулу с использованием логарифма.

[math]\theta^* = \underset{\theta}{\operatorname{argmax}} \log \displaystyle \prod_i p_{model}(x_i;\theta) = \underset{\theta}{\operatorname{argmax}} \displaystyle \sum_i \log p_{model}(x_i;\theta) [/math]

Важен и другой взгляд на то же самое: максимизация правдоподобия эквивалентна минимизации расстояния Кульбака-Лейблера между распределением [math]р[/math], которое получается из нашей модели, и распределением [math]\hat{p}_{data}[/math] — эмпирическим распределе­нием данных. Это эмпирическое распределение попросту полностью сосредоточе­но в точках из набора данных и равномерно распределено по ним, так что:

[math]KL(\hat{p}_{data}(x), p(x; \theta)) = \int \hat{p}_{data}(x) \log p(x; \theta) = \displaystyle \sum_i \hat{p}_{data}(x_i) \log p(x_i; \theta)[/math]

и минимизация этого выражения эквивалентна максимизации того, что выше.

Таксономия порождающих моделей

Таксономия порождающих моделей

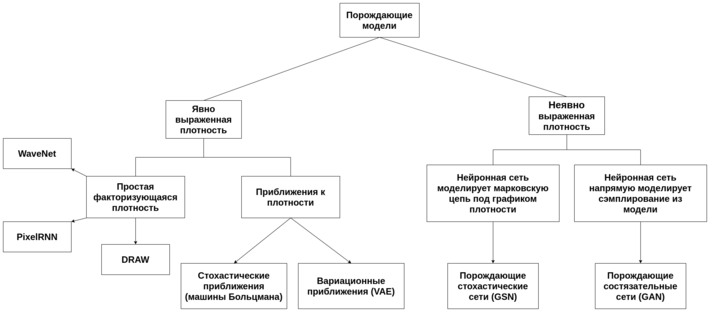
Генеративные модели различаются как раз тем, как именно они строят рас­пределение [math]p(x; \theta)[/math].

Явный подход

Можно строить это распределение явно, делая вероятностные предположения, которые обычно сводятся к тому, что общее распределение [math]p(x; \theta)[/math] выражается в виде произведения тех или иных распределений.

Как правило, модели, где плотность известна явно, делают какие-то дополни­тельные предположения на структуру этих распределений.

Например, байесовские сети строят распределение из условных распре­делений [math]\mathrm P(X_1, \ldots, X_n) = \prod_{i=1}^n \mathrm P(X_i \mid \operatorname{parents}(X_i)).[/math]

Можно даже и вовсе никаких предположений не делать: любое распределение всегда раскладывается как:

[math]p(x) = \displaystyle \prod_{i} p(x_i \mid x_1, {{...}}, x_{i-1})[/math]

Так представляется модель в FVBN (fully visible belief net­works), идея которых состоит в том, что с одномерными распределениями нетрудно разобраться - в ранних работах их представляли классическими моделями. А сейчас мы можем их промоделировать последовательно глу­бокими сетями, получится модель, которая сможет последовательно породить [math]х[/math] компонент за компонентом, каждый раз для порождения [math]x_i[/math] опираясь на уже порожденные [math]x_1, {{...}}, x_{i-1})[/math].

Именно эта идея лежит в основе моде­ли для работы со звуком WaveNet^{[на 24.02.20 не создан]}, разработанной Google DeepMind. Существующие параметрические модели синтезирования речи обычно генерируют звук, прогоняя выходной сигнал через специальные обработчики, называемые вокодерами.

Устройство WaveNet

WaveNet меняет парадигму, генерируя звуковой сигнал по семплам. Это не только приводит к более натуральному звучанию речи, но и позволяет создавать любые звуки, включая музыку. Эта ар­хитектура состоит из нескольких последовательных слоев разреженных сверток и в ней снова встречаются остаточные связи, связи «через уровень» и так далее. Во время обучения входящие последовательности представляют собой звуковые волны от примеров записи голоса. После тренировки можно с помощью сети генерировать синтетические фразы. На каждом шагу семплирования значение вычисляется из вероятностного распределения, посчитанного сетью. Затем это значение возвращается на вход и делается новое предсказание для следующего шага.

В моделях PixelRNN^{[на 24.02.20 не создан]} и PixelCNN^{[на 24.02.20 не создан]} строится изображение пиксель за пикселем, слева направо и свер­ху вниз. Каждый пиксель [math]x_n[/math] порождается из условного распределе­ния [math]p(x_n \mid x_1, {{...}}, x_{n-1})[/math] а оно уже моделируется или [[Рекуррентные нейронные сети|рекуррентной сетью] или сверточной.

Модель DRAW^{[на 24.02.20 не создан]} последо­вательно «рисует» картинку с помощью рекуррентной сети, а механизм внимания^{[на 24.02.20 не создан]} помогает сети в данный момент сконцентрироваться на нужной части изображе­ния.

Если хочется явно выразить совсем сложные распределения в порождающих моделях, их приходится приближать более простыми, которые уже, в свою очередь, могут быть выражены явно. Для этого обычно используются вариационные мето­ды.

Неявный подход

Основная альтернатива всему этому состоит в том, чтобы использовать неявные порождающие модели, в которых мы не пытаемся получить функцию, подсчитывающую плотность нужного распределения в каждой точке, а просто мо­делируем то, что нам от этой модели нужно. Например, если мы хотим просто научиться порождать фото­графии милых котиков, нам не так важно иметь явную функцию плотности [math]p(x)[/math], которая могла бы сказать, насколько вероятно, что перед нами котик, - вполне до­статочно просто уметь генерировать новые [math]x \sim p(x)[/math].

Сэмплирование из сложных многомерных распределений делается с помощью МСМС-методов: попробуем построить мар­ковскую цепь, которая описывает случайное блуждание под графиком плотности распределения. Если достаточно долго блуждать под графиком плотности [math]p(x)[/math], можно будет считать, что полученная точка представляет собой случайную точ­ку, взятую по распределению [math]p(x)[/math]. Примером такого моделирования глубокой сетью являются порождающие стохастические сети(англ. Generative Stochastic Networks)

Глубокие порождающие модели на основе нейронных сетей

• Порождающие состязательные сети
• Автокодировщик
• Вариационный автокодировщик

См. также

• Наивный байесовский классификатор(простейшая порождающая модель)

Примечания

• Примеры генерации паролей на основе исходного распределения

Источники информации

• Generative_model
• Google courses с примерами на понимание
• NIPS 2016 Tutorial: Generative Adversarial Networks(Ian Goodfellow, 2016)
• Николенко С., Кадурин А., Архангельская Е. Глубокое обучение. СПб.: Питер, 2018.