Настройка гиперпараметров
Содержание
Гиперпараметры
Гиперпараметры - параметры, которые не настраиваются во время обучения модели.
Пример гиперпараметра - шаг градиентного спуска, он задается перед обучением.
Пример параметров - веса градиентного спуска, они изменяются и настраиваются во время обучения.
Для подбора гиперпараметров необходимо разделить датасет на три части:
- training set (тренировочный набор данных, для обучении модели)
- validation set (валидационный набор данных, для расчета ошибки и выбора наилучшей модели)
- test set (тестовый набор данных, для тестирования лучшей модели)
Зачем нам нужен и валидационный, и тестовый набор?
Дело в том, что модель может переучиться на валидационном наборе данных. Для выявления переобучения используется тестовый набор данных.
Рассмотрим модель KNeighborsClassifier из библиотеки sklearn.
Техники настройки гиперпараметров
Grid search
Принимает на вход модель и различные значения гиперпараметров (сетку гиперпараметров). Далее, для каждого возможного сочетания значений гиперпараметров, метод считает ошибку и в конце выбирает сочетание, при котором ошибка минимальна.
Пример использования Grid search из библиотеки scikit-learn:
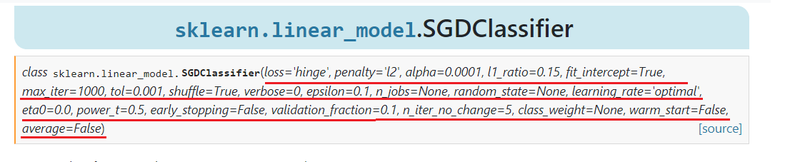
- Создание экземпляра класса SGDClassifier (из sklearn)
- Создание сетки гиперпараметров. В данном случае будем подбирать коэффициент регуляризации, шаг градиентного спуска, количество итераций и параметр скорости обучения.
- Создание экземпляра класса кросс-валидации.
- Создание экземпляра GridSearch (из sklearn). Первый параметр - модель, второй - сетка гиперпараметров, третий - функционал ошибки (используемый для контроля качества моделей по технику кросс-валидации), четвертый - кросс-# # # валидация (можно задать количество фолдов, а можно передать экземпляр класса кросс - валидации)
- Запуск поиска по сетке.
здесь будет картинка
Важные атрибуты GridSearch
- best_estimator_ - лучшая модель
- best_score_ - ошибка, полученная на лучшей модели.
- best_params_ - гиперпараметры лучшей модели
картинка
- cv_results_ - результаты всех моделей.
картинка
- доступ к массиву определенного параметра:
картинка
Реализация
- Katib
- scikit-learn
- Tune
- Talos
Random grid search
Вместо полного перебора, Random grid search работает с некоторыми, случайным образом выбранными, комбинациями. На основе полученных результатов,происходит сужение области поиска. Random grid search будет гораздо полезнее, чем grid search в ситуации, когда гиперпараметров много, но сильно влияющих на конечную производительность алгоритма - мало.
Реализация
- hyperopt
- Katib
- scikit-learn
- Tune
- Talos
SMBO
SMBO - Sequential Model-Based Optimization (Методы последовательной оптимизации на основе моделей)
SMBO являются формализацией байесовской оптимизации.
На каждом шаге SMBO:
- SMBO выбирает текущий набор гиперпараметров на основе предыдущих результатов и Байесовский рассуждений. Делается это для того, чтобы сузить область поиска и сосредоточиться на том, что наиболее перспективно.
- происходит запуск модели с текущими гиперпараметрами
- обновляется вероятностная модель.
Существует пять ключевых аспектов SMBO:
- Сетка значений гиперпараметров (область поиска)
- Целевая функция, которая принимает гиперпараметры и выводит оценку, которую мы хотим минимизировать (или максимизировать)
- Вероятностная модель целевой функции
- Критерий, называемый функцией выбора, для оценки того, какие гиперпараметры выбрать следующим из вероятностной модели.
- История, состоящая из пар <оценка, гиперпараметр>, используемая алгоритмом для обновления вероятностной модели.
Существует несколько вариантов SMBO оптимизации, которые отличаются между собой в 3 и 4 пунктах: есть различные варианты построения вероятностной модели целевой функции и выбора критерия. Вероятностные модели (3 пункт): Gaussian Processes, Random Forest Regressions, and Tree Parzen Estimators (TPE). Популярный критерий (4 пункт): Expected Improvement
TPE
TPE - Tree-structured Parzen Estimator (Древовидная структура Парзена)
Методы SMBO отличаются тем, как они строят вероятностную модель p (y | x). В случае TPE, используется следующая функция:
формула
SMAC
расширяет подходы SMBO
В частности, разработаны подходы обработки данных:
- дискретные и условные пространства параметров (с учетом
оптимизация параметров категориального алгоритма и параметров, между которыми существуют зависимости);
- существенный негауссовский шум (из-за дисперсии в
распределение времени выполнения алгоритма по экземплярам задач и несколько независимых запусков на одном экземпляре);
- частично цензурированные оценки функций (из-за преждевременного
завершенные запуски алгоритма);
- бюджет на общее время, доступное для настройки алгоритма, а не на количество оценок функций;