Материал из Викиконспекты
В этом разделе будут описаны унарные операции в рамках реляционной алгебры. В соответствии с определением, для каждой операции указывается способ построения заголовка, тела отношения, а так же условий применимости, если такие есть.
| Определение: |
[math]\pi_{a_1, a_2, \ldots, a_n}(A)[/math] — проекция отношения [math]A[/math] на аттрибуты [math]a_1, a_2, \ldots, a_n[/math].
Заголовок результирующего отношения: пересечение заголовка [math]A[/math] с [math]\{a_1, a_2, \ldots, a_n\}[/math].
Тело: пересечение кортежей тела [math]A[/math] c [math]\{a_1, a_2, \ldots, a_n\}[/math]. |
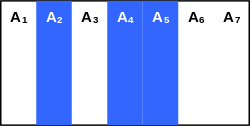
Пояснение определения для [math]\pi_{A_2, A_4, A_5}(A)[/math]:
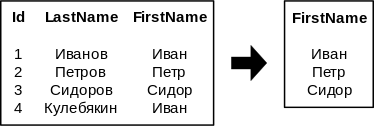
Примеры
- [math]\pi_{FirstName, LastName}[/math]

- [math]\pi_{FirstName}[/math]
Фильтрация
| Определение: |
[math]\sigma_{condition}(A)[/math] — фильтрация отношения [math]A[/math] по условию.
Заголовок результирующего отношения равен заголовку исходного.
Тело: кортежи, удовлетворяющие заданному условию. |
Пояснение к определению:

Примеры
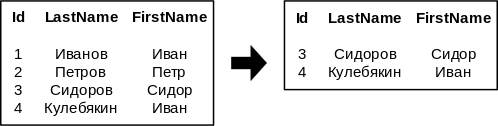
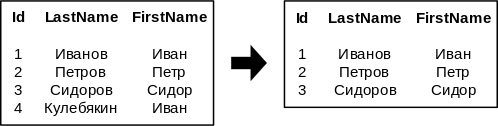
- [math]\sigma_{Id \gt 2}[/math]
- [math]\sigma_{Id \gt 2 \wedge FirstName=Иван}[/math]
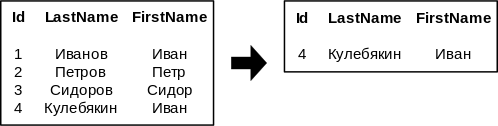
- [math]\sigma_{length(FirstName) + 2 \geq length(LastName)}[/math]
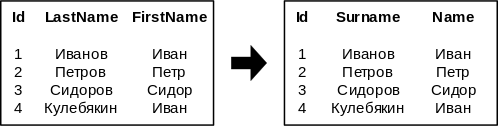
Переименование
| Определение: |
[math]\rho_{NewName_i = OldName_i}(A)[/math] — изменение имени атрибута.
Заголовок результирующего отношения равен заголовку исходного с точностью до изменения названий [math]OldName_i[/math] на [math]NewName_i[/math].
Тело: такое же, как в [math]A[/math], название атрибутов [math]OldName_i[/math] заменено на [math]NewName_i[/math]. |
Примеры
- [math]\rho_{Name=FirstName, Surname=LastName}[/math]