Мост, эквивалентные определения

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Пусть [math] G [/math] — связный граф.

Определение:

Мост (англ. bridge) графа [math]G[/math] — ребро, соединяющее две компоненты реберной двусвязности [math]G[/math]. [math](1)[/math]

Граф [math]G[/math]

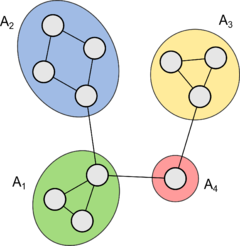
Пример графа с тремя мостами

Эквивалентные определения

Определение:

Мост графа [math]G[/math] — ребро, при удалении которого граф [math]G[/math] становится несвязным. [math](2)[/math]

Определение:

Ребро [math]x[/math] является мостом графа [math]G[/math], если в [math]G[/math] существуют такие вершины [math]u[/math] и [math]v[/math], что любой простой путь между этими вершинами проходит через ребро [math]x.[/math] [math](3)[/math]

Определение:

Ребро [math]x[/math] является мостом графа [math]G[/math], если существует разбиение множества вершин [math]V[/math] на такие множества [math]U[/math] и [math]W[/math], что [math]\forall u \in U[/math] и [math]\forall w \in W[/math] ребро [math]x[/math] принадлежит любому простому пути [math]u \rightsquigarrow w[/math]. [math](4)[/math]

Теорема:

Определения (1), (2), (3) и (4) эквивалентны.

Доказательство:

[math]\triangleright[/math]

[math](1) \Rightarrow (2)[/math] Пусть ребро [math]x[/math] соединяет вершины [math]a[/math] и [math]b[/math]. Пусть граф [math] G - {x} [/math] — связный. Тогда между вершинами [math]a[/math] и [math]b[/math] существует еще один путь, т.е. между вершинами [math]a[/math] и [math]b[/math] существуют два реберно-непересекающихся пути. Но тогда ребро [math]x[/math] не является мостом графа [math]G[/math]. Противоречие. [math](2) \Rightarrow (4)[/math] В условиях определения (4) пусть существуют такие вершины [math]u[/math] и [math]w[/math], что между ними существует простой путь [math]P: x \notin P[/math]. Но тогда граф [math]G - {x}[/math] — связный. Противоречие. [math](4) \Rightarrow (3)[/math] Возьмем [math]\forall u \in U[/math] и [math]\forall w \in W [/math]. Тогда [math]\forall[/math] простой путь [math]u \rightsquigarrow w[/math] содержит ребро [math]x[/math]. Утверждение доказано [math](3) \Rightarrow (1)[/math] Пусть [math](a, b) = x[/math]. Пусть ребро [math]x[/math] не является мостом по определению (1). Тогда между вершинами [math]a[/math] и [math]b[/math] есть простой путь [math]P : P \cap x = \varnothing[/math]. Составим такой путь [math]Q[/math], что [math]Q = ((u \rightsquigarrow a ) \circ P \circ (b \rightsquigarrow w)) [/math]. Сделаем путь [math]Q[/math] простым. Получим простой путь [math](u \rightsquigarrow w)[/math], не проходящий по ребру [math]x[/math]. Противоречие.

[math]\triangleleft[/math]

См.также

• Точка сочленения, эквивалентные определения
• Использование обхода в глубину для поиска мостов

Источники информации

• Харари Ф. Теория графов. М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.)