Расширенные биномиальные коэффициенты
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
| Определение: |
| В математике биномиальные коэффициенты — коэффициенты в разложении бинома Ньютона по степеням . |
Коэффициенты при обозначаются и вычисляются по формуле
.
Значение выражения определено при целых неотрицательных и . Однако видно, что дробь можно сократить на .
.
В этом выражении может принимать произвольные действительные значения.
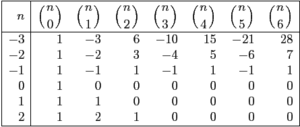
Расширение треугольника Паскаля
Нетрудно проверить, что для биномиальных коэффициентов справедливо равенство:
.
При этом . Это свойство позволяет продлить треугольник Паскаля в сторону отрицательных значений , причём единственным образом.
Применение
Расширенный треугольник Паскаля позволяет раскладывать в ряд простые дроби.
Например, .
В общем случае .
См. также
Источники информации
- Расширенные биномиальные коэффициенты
- Биномиальный коэффициент — Википедия
- Вайнштейн Ф., Разбиение чисел. Журнал "Квант" № 11, 1988 год
- Производящие функции
- Wikipedia — Generating function
- Нахождение количества разбиений числа на слагаемые. Пентагональная теорема Эйлера
- Graham, Knuth, and Patashnik: Concrete Mathematics