NP-полнота игры Тетрис

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Тетрис — популярная игра, созданная в середине 1980-х математиком Алексеем Пажитновым.

Формальные правила

Игровое поле — расчерченный на клетки прямоугольник размером [math]m[/math] горизонтальных рядов (строк) на [math]n[/math] вертикальных (столбцов). Примем следующую индексацию: снизу вверх и слева направо. [math]\langle i, j \rangle[/math]-я клетка либо свободна, либо занята. В допустимом состоянии поля ни один горизонтальный ряд не заполнен целиком и нет ни одной полностью пустой строки, которая бы лежала ниже занятой клетки. При оценке допустимости некоторых действий будем считать, что все клетки вне игрового поля всегда заняты и тем самым ограничивают поле.

SQ

LG

RG

LS

RS

I

T

Игровые фигуры — семь различных фигур, получаемых соединением четырех единичных клеток по каким-либо из сторон. Каждая фигура имеет центр (на илл. 2). Состояние фигуры [math]P[/math] — кортеж из четырех элементов, а именно:

1. тип фигуры — SQ (square), LG (left gun), RG (right gun), LS (left snake), RS (right snake), I или T.
2. ориентация — поворот на 0°, 90°, 180° или 270° по часовой стрелке относительно базовой ориентации фигуры (на илл. 1).
3. позиция центра фигуры на поле, выбираемая из [math]\{1,\dots,m\} \times \{1,\dots,n\}[/math]. Позицией SQ считается местоположение ее левой верхней клетки, так как ее центр лежит на границе четырех клеток, а не внутри одной.
4. значение зафиксирована (англ. fixed) или не зафиксирована (англ. unfixed), определяющее, может ли фигура продолжать двигаться.

В исходном состоянии фигуры она имеет базовую ориентацию, ее позиция такова, что верхний ряд ее клеток содержится в ряду [math]m[/math], а центр в столбце [math]\lfloor n/2 \rfloor[/math], и она не зафиксирована.

Поворот фигуры. Модель поворота — функция [math]R : \langle P,\theta,B \rangle \mapsto P'[/math], где [math]P[/math] и [math]P'[/math] — состояния фигуры, [math]\theta \in \{-90^{\circ},90^{\circ}\}[/math] — угол поворота, а [math]B[/math] — игровое поле. На [math]R[/math] налагаются следующие условия:

1. Если [math]P = \langle t,o,\langle i,j \rangle,f\rangle[/math] и поворот допустим, то [math]P' = \langle t,(o + \theta) \mod 360^{\circ},\langle i',j' \rangle,f\rangle[/math] для некоторых [math]i'[/math] и [math]j'[/math]. Если поворот недопустим, то [math]P' = P[/math].
2. При определении допустимости поворота, [math]R[/math] рассматривает окрестность констатного размера у фигуры [math]P[/math] — то есть, только клетки на заданном расстоянии от позиции [math]P[/math] влияют на [math]R[/math], а положение фигуры на игровом поле значения не имеет.
3. Если все клетки в окрестности [math]P[/math] свободны, то поворот допустим.
4. Если поворот допустим, то [math]P'[/math] не занимает ни одной клетки, уже занятой в [math]B[/math].

Игровые действия.

Для фигуры [math]P=\langle t,o,\langle i,j \rangle , fixed \rangle.[/math] допустимых действий нет. Для фигуры [math]P=\langle t,o,\langle i,j \rangle , unfixed \rangle.[/math] на данном игровом поле [math]B[/math] допустимы следующие действия:

1. Поворот по часовой стрелке. Новым состоянием фигуры будет [math]R(P,90^{\circ},B)[/math].
2. Поворот против часовой стрелки. Новым состоянием фигуры будет [math]R(P,-90^{\circ},B)[/math].
3. Сдвиг влево. Если клетки слева от фигуры свободны в [math]B[/math], фигура [math]P[/math] может быть сдвинута влево на один столбец. Новым состоянием фигуры будет [math]\langle t,o,\langle i,j - 1 \rangle , unfixed \rangle.[/math]
4. Сдвиг вправо. Аналогично сдвигу влево; новым состоянием будет [math]\langle t,o,\langle i,j + 1 \rangle , unfixed \rangle.[/math]
5. Снижение на один ряд, если все клетки под фигурой свободны в [math]B[/math]. Новое состояние — [math]\langle t,o,\langle i - 1,j \rangle , unfixed \rangle.[/math]
6. Фиксация, если хотя бы одна клетка под фигурой занята в [math]B[/math]. Новое состояние — [math]\langle t,o,\langle i,j \rangle , fixed \rangle.[/math]

Траекторией [math]\sigma[/math] фигуры [math]P[/math] называется последовательность допустимых действий, начинающихся в исходном состоянии и заканчивающихся действием-фиксацией. Результатом траектории фигуры [math]P[/math] на игровом поле [math]B[/math] является новое поле [math]B'[/math], определяемое следующим образом:

1. Новое поле [math]B'[/math] — это поле [math]B[/math] с заполненными клетками фигуры [math]P[/math].
2. Если фигура зафиксирована таким образом, что для некоторого горизонтального ряда [math]r[/math] каждая клетка [math]r[/math] в поле [math]B'[/math] заполнена, то ряд [math]r[/math] освобождается. Для всех [math]r' \geqslant r[/math] следует заменить ряд [math]r'[/math] в [math]B'[/math] рядом [math]r'+1[/math] в [math]B'[/math]. Ряд [math]m[/math] в [math]B'[/math] становится пустым. Фиксация одной фигуры может привести к освобождению более чем одного ряда.
3. Если исходное состояние следующей фигуры в [math]B'[/math] заблокировано, игра заканчивается (игрок проигрывает).

Для игры [math]\langle B_0,P_1,\dots,P_p \rangle[/math], последовательностью траекторий [math]\Sigma[/math] является такая последовательность [math] B_0,\sigma_1,B_1,\dots,\sigma_p,B_p[/math], что для любого [math]i[/math] траектория фигуры [math]P_i[/math] на поле [math]B_{i-1}[/math] приводит к полю [math]B_i[/math]. Однако, если существует действие [math]\sigma_q[/math] при некотором [math]q \leqslant p[/math], приводящее к проигрышу, то последовательность [math]\Sigma[/math] завершается на [math]B_q[/math], а не на [math]B_p[/math].

NP-полнота игры

Рассмотрим следующую проблему, называемую k-cleared rows ([math]G,\Sigma[/math]): в игре [math]G[/math], приводит ли [math]\Sigma[/math] к освобождению хотя бы [math]k[/math] рядов до проигрыша? Вспомним проблему 3-Partition, которая является NP-полной. Формальное ее условие таково: ввод — последовательность целых чисел [math]a_1,a_2,\dots,a_{3s}[/math] и неотрицательное число [math]T[/math] такое, что [math]T/4 \lt a_i \lt T/2[/math] для всех [math]1\leqslant i \leqslant 3s[/math], [math]\sum_{i=1}^{3s} a_i = sT[/math]; вывод — можно ли [math]\{a_1,\dots,a_{3s}\}[/math] разбить на [math]s[/math] непересекающихся подмножеств [math]A_1,\dots,A_s[/math] так, что для всех [math]1\leqslant j \leqslant s[/math] выполняется [math]\sum_{a_i \in A_j} a_i = T[/math].

Теорема:

3-Partition сводится к k-cleared rows.

Доказательство:

[math]\triangleright[/math]

Опишем отображение из 3-Partition в k-cleared-rows. Для заданного ввода 3-Partition [math]P = \langle a_1,\dots,a_{3s},T \rangle[/math], составим игру [math]G(P)[/math], поле которой может быть полностью очищено, только если для [math]P[/math] в задаче 3-Partition ответ положительный. Начальное игровое поле Начальное игровое поле содержит [math]s[/math] контейнеров, соответствующих множествам [math]A_1,\dots,A_s[/math] в задаче 3-Partition. Последовательность фигур состоит из некоторого числа фигур, соответствующих каждому из [math]a_i[/math] и подобранных так, что все фигуры для [math]a_i[/math] должны быть помещены в один и тот же контейнер. Существует подходящее решение задачи 3-Partition для [math]\{a_1,\dots,a_{3s}\}[/math] в том и только том случае, когда наборы фигур во всех контейнерах имеют одинаковую высоту. Последние три столбца в игровом поле представляют собой стопор, который не дает очистить ряды, пока не подойдет к концу последовательность фигур; если все контейнеры заполнены на одинаковую высоту, то все поле может быть очищено с помощью последней (завершающей) части последовательности. Игра [math]G[/math] состоит из следующих компонент: Начальное игровое поле. Поле имеет [math]6T + 22 + (3s + O(1))[/math] строк и [math]6s + 3[/math] столбцов. Каждое [math]a_i[/math] будет представлено [math]a_i + 1[/math] блоками размером [math]6 \times 6 [/math]; так как сумма элементов [math]A_j = \{a_i,a_j,a_k\}[/math] равна [math]T[/math], получаем [math]6(T+3)=6T+18[/math]. В дополнение к этим [math]6T+18[/math] рядам, внизу находятся четыре ряда, обеспечивающие корректное положение блокам. 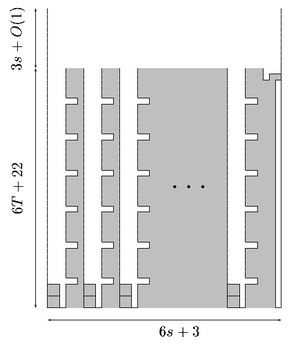Верхние [math]3s+O(1)[/math] рядов ([math]O(1)[/math] — это размер окрестности в модели вращения) изначально пусты и представляют собой промежуточную зону, где фигуру можно вращать и двигать, прежде чем она попадет в нижние [math]6T+22[/math] рядов. Остальная часть поля может быть логически разделена на [math]s+1[/math] части, где первые [math]s[/math] частей имеют шесть клеток в ширину, а последняя — три клетки в ширину. Первые [math]s[/math] частей — это контейнеры, имеющие следующий вид: В первом и втором столбцах пусты все клетки, кроме нижних четырех. Третий столбец не имеет занятых клеток. В четвертом и пятом столбцах пусты только клетки в тех строках, чей номер по модулю 6 равен 5. Шестой столбец не имеет пустых клеток. Последняя логическая часть — стопор шириной в три клетки: В первом столбце заполнены все клетки, кроме двух верхних. Во втором столбце заполнены все клетки, кроме верхней. В третьей колонке пусты все клетки, кроме второй сверху. Фигуры. Последовательностью фигур для всей игры будет конкатенация последовательностей для каждого [math]a_i[/math] и завершающей последовательности. Для каждого числа [math]a_1,\dots,a_{3s}[/math] имеем следующие части: Инициатор — последовательность [math]\langle I,LG,SQ \rangle[/math]. Наполнитель — последовательность [math]\langle LG,LS,LG,LG,SQ \rangle[/math], повторенная [math]a_i[/math] раз. Завершитель— последовательность [math]\langle SQ,SQ \rangle[/math]. Вышеописанные части подаются для [math]a_1,a_2,\dots[/math] последовательно. После частей, соответствующих [math]a_{3s}[/math], идет завершающая последовательность: [math]s[/math] фигур [math]I[/math] подряд. одна фигура [math]RG[/math]. [math]3T/2 + 5[/math] фигур [math]I[/math] подряд. //продолжение

[math]\triangleleft[/math]

Источники информации

• «Tetris is Hard, Even to Approximate» by Erik D. Demaine, Susan Hohenberger, David Liben-Nowell