Реляционная алгебра: операции над множествами
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
В этом разделе будут описаны операции над множествами в рамках реляционной алгебры. В соответствии с определением, для каждой операции необходимо указать способ построения заголовка, тела отношения, а также условия применимости, если такие есть.
Простые операции
Из теории множеств в реляционную алгебру естественным образом переходят операции:
- — объединение;
- — пересечение;
- — разность.
Эти операции по определению применимы только к отношениям с одинаковыми заголовками. В результате получается отношение с таким же заголовком и телом, полученным в соответствии с множественной операцией. Иначе говоря, заголовок остается тем же, а над телами отношений производится соответствущая множественная операция (объединение, пересечение, вычитание и прочие).
Примеры
- Объединение отношений:
Как и в случае множественных операций, дубликаты учитываются ровно по одному разу.
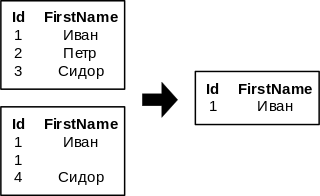
- Пересечение отношений:
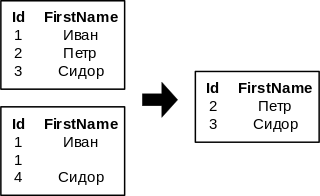
- Разность отношений:
Стоит отметить, что для объединения отношений с различающимися именами атрибутов, но при равном их количестве, можно воспользоваться переименованием для того, чтобы привести заголовки к одному виду.