Классы NC и AC

Определения

Определение:

[math]\mathrm{NC^i}[/math]— множество языков, которые распознаются семейством логических схем размера полином от [math]n[/math] и глубины [math]O(log^i (n))[/math], где [math]n[/math] — длина входа; степень входа элемента не больше двух. Причем существует детерминированная машина Тьюринга, строящая такую схему по [math]1^n[/math], используя [math]O(log(n))[/math] ячеек памяти.

Определение:

[math]\mathrm{AC^i}[/math] определяется аналогично [math]\mathrm{NC^i}[/math], только степень входа элемента неограничена.

Определение:

[math]\mathrm{NC} = \bigcup \limits_{i = 0}^{\infty} \mathrm{NC^i}[/math].

Определение:

[math]\mathrm{AC} = \bigcup \limits_{i = 0}^{\infty} \mathrm{AC^i}[/math].

Теоремы

Теорема:

[math]\mathrm{NC^i} \subset \mathrm{AC^i} \subset \mathrm{NC^{i+1}}[/math]

Доказательство:

[math]\triangleright[/math]

[math]\mathrm{NC^i} \subset \mathrm{AC^i}[/math] Это понятно из определения [math]\mathrm{NC^i}[/math] и [math]\mathrm{AC^i}[/math]. [math]\mathrm{AC^i} \subset \mathrm{NC^{i+1}}[/math] Пусть [math]L \in \mathrm{AC^i}[/math]. [math]L[/math] распознается семейством схем [math]C_n[/math] полиномиального размера. Значит, степень входа элементов схемы [math]C_n[/math] — это полином от [math]n[/math]. 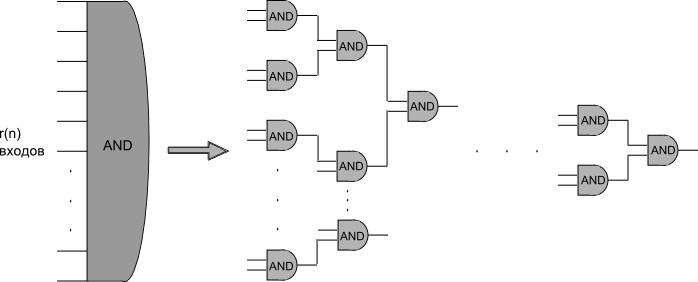Заменим элементы схемы [math]C_n[/math] элементами со степенью входа не более двух следующим образом: При замене каждого такого элемента глубина схемы увеличивается не более чем в [math]log_2 r(n) = O(log(n))[/math], а так как изначально глубина схемы была [math]O(log^i(n))[/math], то после замены всех элементов глубина схемы станет [math]O(log^i(n)) \cdot O(log(n)) = O(log^{i+1}(n))[/math]. Так как при замене элемента мы добавляем не более [math]r(n)[/math] элементов, а изначально размер схемы был полиномиальным и каждый ее элемент мы заменили на полином элементов, то после всех замен размер схемы остался полиномиальным.

[math]\triangleleft[/math]

Следствие: [math]\mathrm{NC} = \mathrm{AC}[/math]

Теорема:

[math]\mathrm{NC} \subseteq \mathrm{P}[/math]

Доказательство:

[math]\triangleright[/math]

Пусть [math]L \in \mathrm{NC}[/math]. Тогда [math]L[/math] распознается некоторым семейством схем [math]C_n[/math], таких, что существует детерминированная машина Тьюринга, строящая такую схему по [math]1^n[/math], используя [math]O(log(n))[/math] ячеек памяти. Конфигурация МТ задается положением головки и состоянием ячеек памяти, то есть у МТ может быть [math]n \cdot 2^{O(log(n))} = O(n^2)[/math] конфигураций. При построении схемы конфигурации не могут повторяться, иначе МТ зациклится, следовательно схема будет построена за полиномиальное от [math]n[/math] время. Построим для данного входа схему и вычислим ее. На вычисление схемы потребуется полином времени, так как схема полиномиального размера.

[math]\triangleleft[/math]

Равенство [math]\mathrm{NC}[/math] и [math]\mathrm{P}[/math] — неразрешенная на данный момент задача.

Теорема:

[math]L[/math] распознается параллельным компьютером с [math]O(poly(n))[/math] процессоров за время [math]O(poly(log(n)) \Leftrightarrow L \in \mathrm{NC}[/math].

Доказательство:

[math]\triangleright[/math]

Пусть [math]L \in \mathrm{NC}[/math]. [math]L[/math] распознается семейством схем [math]C_n[/math], где [math]C_n[/math] размера [math]N=O(poly(n))[/math] и имеет глубину [math]O(log^d n)[/math]. Тогда возьмем параллельный компьютер с [math]N[/math] процессорами, где каждый из них будет играть роль одного элемента схемы. Так как компьютер параллельный, то вычисления на каждом уровне схемы будут выполнятся параллельно. Тогда получаем, что всего потребуется [math]O(log^d(n))[/math] времени. Пусть [math]L[/math] распознается параллельным компьютером с [math]N=O(poly(n))[/math] процессоров за время [math]D=O(log^d n)[/math]. Тогда построим схему глубины [math]D[/math], на каждом уровне которой будет по [math]N[/math] элементов, таких, что [math]i[/math]-й элемент на уровне [math]t[/math] выполняет вычисления, производимые [math]i[/math]-м процессором в момент времени [math]t[/math]. Всего в схеме будет [math]N \cdot D = O(poly(n)) \cdot O(log^d n) = O(poly(n))[/math] элементов.

[math]\triangleleft[/math]