Основные определения теории графов
Содержание
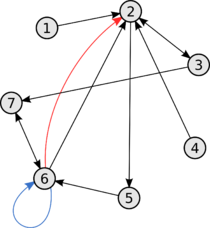
Ориентированные графы
| Определение: |
| Ориентированным графом (англ. directed graph) называется пара , где — множество вершин (англ. vertices), а — множество рёбер. |
| Определение: |
| Конечным графом (англ. finite graph) называется граф, в котором множества и — конечны. Следует заметить, что большинство рассматриваевых нами графов — конечны. |
| Определение: |
| Ребром (англ. edge, дугой (англ. arc), линией (англ. line)) ориентированного графа называют упорядоченную пару вершин . |
| Определение: |
| Изоморфные графы — два графа A и B называются изоморфными, если можно установить биекцию между их вершинами и соответствующими им ребрами. |
В графе ребро, концы которого совпадают, то есть , называется петлей (англ. loop).
Если имеется ребро , то говорят:
- — предок (англ. direct predecessor) .
- и — смежные (англ. adjacent)
- Вершина инцидентна ребру
- Вершина инцидентна ребру
Инцидентность — понятие, используемое только в отношении ребра и вершины. Две вершины или два ребра не могут быть инцидентны.
Граф с вершинами и ребрами называют - графом. -граф называют тривиальным.
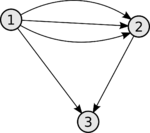
Заметим, что по определению ориентированного графа, данному выше, любые две вершины нельзя соединить более чем одним ребром . Поэтому часто используют другое определение.
| Определение: |
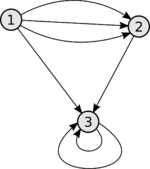
| Ориентированным графом называется четверка , где и — некоторые множества, а . Такой граф иногда называют псевдографом (англ. pseudograph). |
В псевдографе допускается соединять вершины более чем одним ребром. Такие ребра называются кратными (иначе — параллельные, англ. multi-edge, parallel edge). Псевдограф без петель принято называть мультиграфом.
Также для ориентированных графов определяют полустепень исхода вершины (англ. outdegree) и полустепень захода вершины (англ. indegree) .
Стоит отметить, что для ориентированного графа справедлива лемма о рукопожатиях, связывающая количество ребер с суммой степеней вершин.
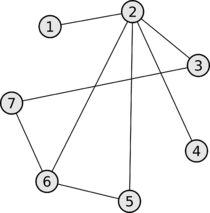
Неориентированные графы
| Определение: |
| Неориентированным графом (англ. undirected graph) называется пара , где — множество вершин, а — множество рёбер. |
| Определение: |
| Ребром в неориентированном графе называют неупорядоченную пару вершин . |
Иное определение:
| Определение: |
| Неориентированным графом называется тройка , где — множество вершин, — множество ребер, а . Это определение, в отличие от предыдущего, позволяет задавать графы с кратными ребрами. |
Степенью (англ. degree, valency) вершины в неориентированном графе называют число ребер, инцидентных . Будем считать, что петли добавляют к степени вершины .
Остальные определения в неориентированном графе совпадают с аналогичными определениями в ориентированном графе.
Представление графов
Матрица и списки смежности
Граф можно представить в виде матрицы смежности (англ. adjacency matrix), где . Также в ячейке матрицы можно хранить вес ребра или их количество (если в графе разрешены паралелльные ребра). Для матрицы смежности существует теорема, позволяющая связать степень матрицы и количество путей из вершины в вершину .
Если граф разрежен (англ. sparse graph, , то есть, неформально говоря, в нем не очень много ребер. Формально говорить не получается, потому что везде разреженные графы определяются по-разному), его лучше представить в виде списков смежности, где список для вершины будет содержать вершины . Данный способ позволит сэкономить память, т.к. не придется хранить много нулей.
Пути в графах
| Определение: |
| Путём (маршрутом,англ. path) в графе называется последовательность вида , где ; — длина пути. |
| Определение: |
| Циклическим путём (англ. closed walk) в ориентированном графе называется путь, в котором . |
| Определение: |
| Циклическим путём в неориентированном графе называется путь, в котором , а так же . |
| Определение: |
| Цикл (англ. integral cycle) — это класс эквивалентности циклических путей на отношении эквивалентности таком, что два пути эквивалентны, если ; где и — это две последовательности ребер в циклическом пути. |
| Определение: |
| Простой (вершинно-простой) путь — путь, в котором каждая из вершин графа встречается не более одного раза. |
| Определение: |
| Реберно-простой путь — путь, в котором каждое из ребер графа встречается не более одного раза. |
| Определение: |
| Длина пути — количество рёбер, входящих в последовательность, задающую этот путь. |
Часто используемые графы
| Определение: |
| — полный граф с вершинами. |
| Определение: |
| — двудольный граф с вершинами в одной доле и во второй. |
См. также
Литература
- Харари Фрэнк Теория графов = Graph theory/Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)
- Wolfram Mathworld: Graph