Straight skeleton

Эта статья находится в разработке!

Существует целый класс структур типа $\mathrm{skeleton}$, которые описывают базовые топологические свойства объектов. Структура $\mathrm{straight}\ \mathrm{skeleton}$ была придумала Oswin Aichholzer. Она используются в различных практических задачах (проектирование крыш для зданий) и для доказательства некоторых теорем.

Топологические свойства

Определение:

Straight skeleton (Angular Bisector Network, ABN) полигона без самопересечений определяет разбиение полигона на регионы, границами которых являются стороны полигона, биссектрисы углов и отрезки, соединяющие точки пересечения биссектрис.

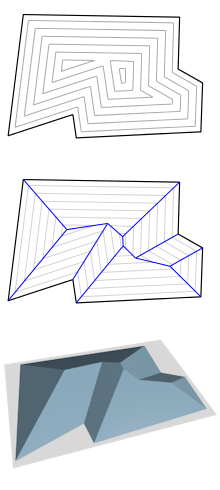
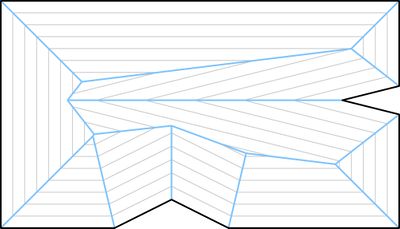
Опишем подробней, как получается такое разбиение. Мы можем представить, будто все стороны прямоугольника параллельно двигаются внутрь с одинаковой постоянной скоростью, то есть многоугольник как бы сжимается внутрь. Тогда вершины будут двигаться вдоль биссектрис , а точки пересечения биссектрис будут соединять совпавшие участки сторон прямоугольника в конце движения. В каждый момент времени от начала движения рёбер мы получаем слоистую структуру (рис 1.). На рис. 2 синим цветом выделен $\mathrm{straight}\ \mathrm{skeleton}$ — множество отрезков, образованных точками пересечения при движении сторон полигона. Чем-то структура похожа на строение крыши в домах (рис. 3). И для решения этой задачи как раз $\mathrm{straight}\ \mathrm{skeleton}$ и может применяться: по стенам здания необходимо спроектировать его крышу.

Проектирование крыши здания по готовым стенам

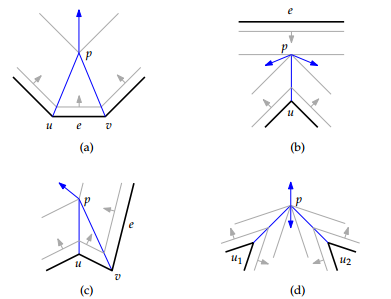
Процесса стягивания многоугольника продолжается до тех пор, пока происходят его топологические изменения, то есть меняется число вершин в стянутом многоугольнике, и таким образом появляются новые вершины дерева $\mathrm{straight}\ \mathrm{skeleton}$. Существуют два типа изменений, в ходе которых образуются новый вершины дерева:

• $Edge\ event$ — данное изменение происходит, когда сторона многоугольника полностью стягивается, делая соседние стороны инцидентными.
• $Split\ event$ происходит, когда ребро разбивается на два новых ребра, исходящих из точки преломления старого. Такое событие происходит на биссектрисе вогнутой вершины многоугольника. И тогда стягиваемая многоугольником область разбивается на две непересекающиеся многоугольные области.

На рисунке $edge\ event'$ы изображён красным кругом, а $split\ event'$ы — чёрным прямоугольником.

Таким образом, $event'$ы соответствуют внутренним вершинам $\mathrm{straight}\ \mathrm{skeleton}$, гранями являются области многоугольника, заметаемые сторонами многоугольника в процессе стягивания, дуги $\mathrm{straight}\ \mathrm{skeleton}$ соединяют либо две внутренние вершины либо внутреннюю вершину с листом — вершиной многоугольника.

Стоит также отметить, что в общем случае $split\ event'$ы могут быть нетривиальными. На рисунке ниже в случае $(c)$ в вершине $p$ совпали $split\ event$ из вершины $u$ и $edge\ event$ ребра $e$, а в случае $(d)$ совпали два $split\ event'$а вершин $u_1$ и $u_2$. Случаи $(a)$ и $(b)$ — простые $edge$ и $split\ event'$ы.

Свойства Straight skeleton

Из процесса построения $\mathrm{straight}\ \mathrm{skeleton}$ следует, что он является планарным графом. Ранее уже упоминалось, что он также является деревом. Будем обозначать $\mathrm{straight}\ \mathrm{skeleton}$ простого полигона без самопересечений $P$, в котором $n$ вершин, как $S(P)$. Тогда справедливы следующие леммы:

Лемма (1):

$S(P)$ является деревом, содержит $n$ граней, не более $n - 2$ внутренние вершины и не более $2 n - 3$ рёбер.

Доказательство:

$\triangleright$

Каждая грань $f(e)$ начинается образовываться во время стягивания ребра $e$, и даже если на ребре произошёл $split\ event$, сама грань не могла разделиться. Построение грани $f(e)$ завершается, когда ребро $e$ полностью стягивается. И это ребро дальше не может появиться снова, поэтому граней в $S(P)$ столько, сколько сторон в многоугольнике, то есть ровно $n$. То, что $S(P)$ является деревом, легко доказывается по индукции. База верна, когда внутренняя вершина всего одна. Тогда у $\mathrm{straight}\ \mathrm{skeleton}$ листьями будут вершины многоугольника. Такой граф очевидным образом будет деревом. Если в $\mathrm{straight}\ \mathrm{skeleton}\ k$ внутренних вершин, то рассмотрим самый первый $edge\ event$. Он закончился в какой-то внутренней вершине $\mathrm{straight}\ \mathrm{skeleton}$, у неё есть смежные листья — вершины, инцидентные этому ребру, — и из неё достижимы другие $\mathrm{straight}\ \mathrm{skeleton}'$ы, с не более чем $k - 1$ внутренними вершинами, и они являются деревьями по предположению индукцию. Тогда получаем, что $S(P)$ для $k$ вершин тоже будет деревом. Внутренние вершины в $\mathrm{straight}\ \mathrm{skeleton}$ имеют степень не меньше $3$ — простой перебор всех случаев $event'$ов (степень будет больше, если в одной вершине совпало несколько событий). Так как $S(P)$ имеет $n$ листьев, то внутренних вершин будет не больше $n - 2$, а так как $S(P)$ является деревом, то рёбер у него будет не более $2 n - 3$.

$\triangleleft$

Wavefront-алгоритм

Существует простой в понимании и реализации алгоритм для построения $\mathrm{straigt}\ \mathrm{skeleton}$ на основе триангуляции, который работает за время $\mathcal{O}(n^3 \log n)$

Рассмотрим оригинальный алгоритм, который был предложен авторами этой структуры.

TODO: "Простой" алгоритм построения за n^3 (wavefront)

Другие алгоритмы

Известен алгоритм построения $\mathrm{straight}\ \mathrm{skeleton}$ для монотонных полигонов за время $\mathcal{O}(n \log n)$ с использованием $\mathcal{O}(n)$ памяти. Существует и более сложный алгоритм, который строит $\mathrm{straight}\ \mathrm{skeleton}$ за время $\mathcal{O}(nm + n \log n)$, где $n$ — общее число вершин в полигоне, $m$ — число вогнутых вершин в полигоне.

Источники информации

• Wikipedia — Straight skeleton
• Computing Straight Skeletons and Motorcycle Graphs: Theory and Practice
• Designing roofs and drawing phylogenetic trees
• Eric Berberich, "Straight Skeleton, Computational Geometry and Geometric Computing Seminar"
• [The Angular bisector network Implementation and the CGAL library]