Красно-черное дерево

Материал из Викиконспекты
Версия от 09:56, 15 мая 2015; Анна (обсуждение | вклад) (→‎Объединение красно-чёрных деревьев)
Перейти к: навигация, поиск

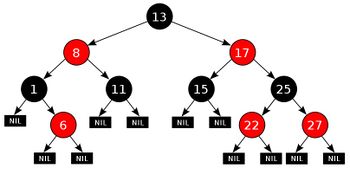
Красно-чёрное дерево (англ. red-black tree) — двоичное дерево поиска, в котором баланс осуществляется на основе "цвета" узла дерева, который принимает только два значения: "красный" (англ. red) и "чёрный" (англ. black).

Пример красно-чёрного дерева.

При этом все листья дерева являются фиктивными и не содержат данных, но относятся к дереву и являются чёрными.

Для экономии памяти фиктивные листья можно сделать одним общим фиктивным листом.

Свойства

Оригинальные

Красно-чёрным называется бинарное поисковое дерево, у которого каждому узлу сопоставлен дополнительный атрибут — цвет и для которого выполняются следующие свойства:

  1. Каждый узел промаркирован красным или чёрным цветом
  2. Корень и конечные узлы (листья) дерева — чёрные
  3. У красного узла родительский узел — чёрный
  4. Все простые пути из любого узла x до листьев содержат одинаковое количество чёрных узлов
  5. Чёрный узел может иметь чёрного родителя

Определим ослабленное красно-чёрное дерево как красно-чёрное дерево, корень которого может быть как чёрным, так и красным. Останется ли оно после этого красно-черным? При добавлении вершины около корня могут возникнуть повороты, и корневая вершина перейдет в какое-то поддерево. Из-за этого может возникнуть ситуация, в которой подряд будут идти две красные вершины. Если мы продолжим вставлять элементы подобным образом, свойства дерева перестанут выполняться и оно перестанет быть сбалансированным. Таким образом, время выполнения некоторых операций ухудшится.

Альтернативные

В книге Кормена "Алгоритмы: построение и анализ" дается немного иное определение красно-черного дерева, а именно:

Двоичное дерево поиска является красно-чёрным, если обладает следующими свойствами:

  1. Каждая вершина — либо красная, либо черная
  2. Каждый лист — черный
  3. Если вершина красная, оба ее ребенка черные
  4. Все пути, идущие от корня к листьям, содержат одинаковое количество черных вершин

То, что только черная вершина может иметь красных детей, совместно с [math]4[/math]-тым свойством говорит о том, что корень дерева должен быть черным, а значит определения можно считать эквивалентными.

Зачем в дереве красные узлы? Если при добавлении вершины маркеровать ее черным цветом, то после некоторых операций свойство [math]4[/math] перестанет выполняться, тогда дерево перестанет быть сбалансированным и превратится в обычное бинарное дерево поиска.

Высота красно-черного дерева

Определение:
Будем называть чёрной высотой (англ. black-height) вершины [math]x[/math] число чёрных вершин на пути из [math]x[/math] в лист, не учитывая саму вершину [math]x[/math].


Лемма:
В красно-черном дереве с черной высотой [math]hb[/math] количество внутренних вершин не менее [math]2^{hb+1}-1[/math].
Доказательство:
[math]\triangleright[/math]
Если рассмотреть лист (фиктивную вершину), то для нее лемма верна. Рассмотрим внутреннюю вершину [math]x[/math]. Пусть [math]hb(x)=h'[/math]. Тогда если ее потомок [math]p[/math] — черный, то высота [math]hb(p)=h'-1[/math], а если красный, то [math]hb(p) = h'[/math]. Таким образом, по предположению индукции, в поддеревьях содержится не менее [math]2^{h'}-1[/math] вершин, а во всём дереве, соответственно, не менее [math]2^{h'}-1 + 2^{h'}-1 + 1=2^{h'+1}-1[/math].
[math]\triangleleft[/math]
Теорема:
Красно-чёрное дерево с [math]N[/math] ключами имеет высоту [math]h = O(\log N)[/math].
Доказательство:
[math]\triangleright[/math]

Так как только черные узлы могут иметь красных детей, то в самом длинном пути от корня до листа красных вершин будет точно не больше половины, поэтому если обычная высота дерева равна [math]h[/math], то черная высота дерева будет не меньше [math]h/2-1[/math] и, по лемме, количество внутренних вершин в дереве

[math]N \geqslant 2^{h/2}-1[/math]

Прологарифмировав неравенство, имеем:

[math]\log(N+1) \geqslant h/2[/math]

[math]2\log(N+1) \geqslant h[/math]

[math]h \leqslant 2\log(N+1)[/math]
[math]\triangleleft[/math]

Операции

Узел, с которым мы работаем, на картинках имеет имя [math]x[/math].

Вставка элемента

Каждый элемент вставляется вместо листа, поэтому для выбора места вставки идём от корня до тех пор, пока указатель на следующего сына не станет [math]nil[/math](то есть этот сын — лист). Вставляем вместо него новый элемент с [math]nil[/math]-потомками и красным цветом. Теперь проверяем балансировку. Если отец нового элемента красный, то достаточно рассмотреть только два случая:

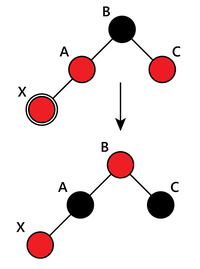
1. "Дядя" этого узла тоже красный. Тогда просто перекрашиваем "отца" и "дядю" в чёрный цвет, а "деда" — в красный. Проверяем, не нарушает ли он теперь балансировку. Если в результате этих перекрашиваний мы дойдём до корня, то в нём в любом случае ставим чёрный цвет.

Untitled-1.png

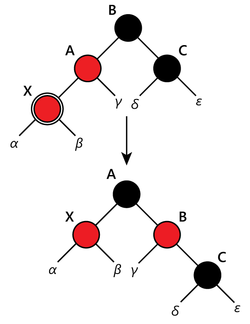
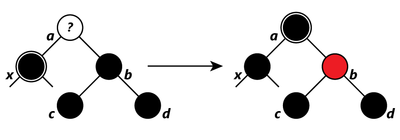
2. "Дядя" чёрный. Если выполнить только перекрашивание, то может нарушиться постоянство чёрной высоты дерева по всем ветвям. Поэтому выполняем поворот. Если добавляемый узел был правым потомком, то необходимо сначала выполнить левое вращение, которое сделает его левым потомком.

Untitled-2.png

Удаление вершины

При удалении вершины могут возникнуть три случая в зависимости от количества её детей:

  1. Если у вершины нет детей, то изменяем указатель на неё у родителя на [math]nil[/math].
  2. Если у неё только один ребёнок, то делаем у родителя ссылку на него вместо этой вершины.
  3. Если же имеются оба ребёнка, то находим вершину со следующим значением ключа. У такой вершины нет левого ребёнка. Удаляем уже эту вершину описанным во втором пункте способом, скопировав её ключ в изначальную вершину.

Проверим балансировку дерева. Так как при удалении красной вершины свойства дерева не нарушаются, то восстановление балансировки потребуется только при удалении чёрной. Рассмотрим ребёнка удалённой вершины.

1. Если брат этого ребёнка красный, то делаем вращение вокруг ребра между отцом и братом, тогда брат становится родителем отца. Красим его в чёрный, а отца - в красный цвет.

Untitled-3.png

2. Если брат текущей вершины был чёрным, то получаем три случая:

  • Оба ребёнка у брата чёрные. Красим брата в красный цвет и рассматриваем далее отца вершины.

Untitled-4.png

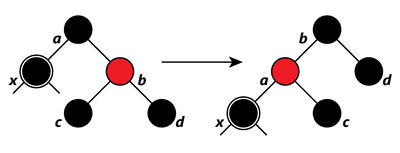
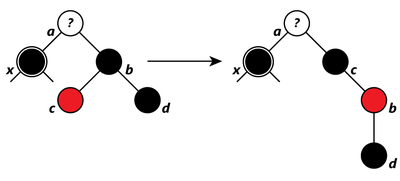
  • Если у брата правый ребёнок чёрный, а левый красный, то перекрашиваем брата и его левого сына и делаем вращение.

Untitled-5.png

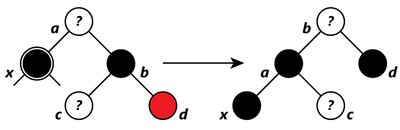
  • Если у брата правый ребёнок красный, то перекрашиваем брата в цвет отца, его ребёнка и отца - в чёрный, делаем вращение и выходим из алгоритма.

Untitled-6.png

Продолжаем тот же алгоритм, пока текущая вершина чёрная и мы не дошли до корня дерева. Из рассмотренных случаев ясно, что при удалении выполняется не более трёх вращений.

Объединение красно-чёрных деревьев

Объединение двух красно-чёрных деревьев [math]T_{1}[/math] и [math]T_{2}[/math] по элементу [math]x[/math] выполняется, когда [math]key[T_{1}] \leqslant x[/math] и [math]x \leqslant key[T_{2}][/math]. Найдём чёрные высоты деревьев. Предположим также, что [math]hb[T_{1}] \geqslant hb[T_{2}][/math]. Тогда в дереве [math]T_{1}[/math] ищем среди чёрных вершин, имеющих чёрную высоту [math]hb[T_{2}][/math], вершину [math]y[/math] с наибольшим ключом. Пусть [math]T_{y}[/math] — поддерево с корнем [math]y[/math]. Объединяем это дерево с [math]T_{2}[/math] в одно с красным корнем [math]x[/math]. Теперь родителем вершины [math]x[/math] становится бывший отец вершины [math]y[/math]. Осталось восстановить свойства красно-черного дерева, чтобы у красной вершины не было красных детей. Делается аналогично алгоритму добавления вершины.

Так как общее время выполнения каждой из операций порядка высоты дерева ,то все они выполняются за [math]O(\log{n})[/math].

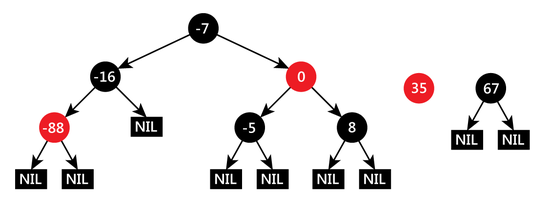
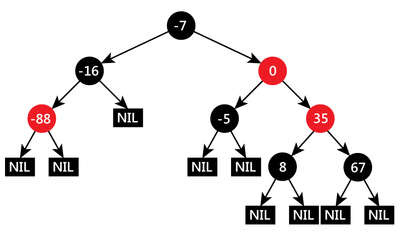
Рассмотрим пример объединения двух красно-чёрных деревьев и вершины[math](35)[/math]:

Untitled-7.png

Узнаём чёрную высоту левого и правого дерева. Чёрная высота левого и правого деревьев равна [math]2[/math] и [math]1[/math] соответственно. Так как чёрная высота левого дерева больше, то ищем в левом дереве чёрную вершину, имеющую чёрную высоту правого дерева, с наибольшим ключом. Чёрная высота вершины[math](8)[/math] левого дерева равна высоте правого дерева и ключ является наибольшим. Поэтому вершина[math](8)[/math] становится левым сыном вершины[math](35)[/math], а правое дерево будет правым сыном. Вершина[math](35)[/math] станет правым сыном вершины[math](0)[/math]:

Untitled-8.png

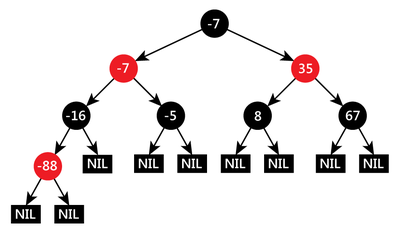
Далее проверяем: не нарушили ли мы свойства красно-чёрного дерева. Так как присутствует нарушение(у красной вершины есть красный сын), то перекрасим вершины и сделаем поворот:

Untitled-9.png

Преимущества красно-чёрных деревьев

При вставке выполняется не более [math]O(1)[/math] вращений.

Алгоритм вставки и удаления может быть написан в один проход сверху вниз, вместо алгоритма, который использует рекурсивный проход вниз, родительские указатели или явный стек для обеспечения возможности пройти назад вверх, чтобы провести перебалансировку.

Процедуру балансировки практически всегда можно выполнять параллельно с процедурами поиска, так как алгоритм поиска не зависит от атрибута цвета узлов.

Сбалансированность этих деревьев хуже, чем у АВЛ, но работа по поддержанию сбалансированности в красно-чёрных деревьях обычно эффективнее. Для балансировки красно-чёрного дерева производится минимальная работа по сравнению с АВЛ-деревьями.

Использует всего 1 бит дополнительной памяти для хранения цвета вершины. Но на самом деле в современных вычислительных системах память выделяется кратно байтам, поэтому это не является преимуществом относительно, например, АВЛ-дерева, которое хранит 2 бита. Однако есть реализации красно-чёрного дерева, которые хранят значение цвета в бите. Пример — Boost Multiindex. В этой реализации уменьшается потребление памяти красно-чёрным деревом, так как бит цвета хранится не в отдельной переменной, а в одном из указателей узла дерева.

Красно-чёрные деревья являются наиболее активно используемыми на практике самобалансирующимися деревьями поиска. В частности, ассоциативные контейнеры библиотеки STL(map, set, multiset, multimap) основаны на красно-чёрных деревьях.

См. также

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Красно-черное_дерево&oldid=46511»