Игра «Жизнь»

Игра «Жизнь» (англ. Conway's Game of Life) — клеточный автомат, придуманный английским математиком Джоном Конвеем в 1970.

Правила

• Действие происходит на бесконечной плоскости, разделенной на клетки
• Каждая клетка может находиться в двух состояниях: быть живой или быть мёртвой
• У каждой клетки [math]8[/math] соседей
• Если клетка жива и у нее [math]2-3[/math] живых соседа, то она остается живой, иначе умирает
• Если клетка мертва и у нее [math]3[/math] живых соседа, то она становится живой, иначе остается мертвой
• Игра прекращается, если на поле не останется ни одной живой клетки
• Игра прекращается, если при очередном шаге ни одна из клеток не меняет своего состояния
• Игра прекращается, если конфигурация на очередном шаге в точности повторит себя же на одном из более ранних шагов

Универсальность

Теорема:

Игра "Жизнь" вычисляет то же множество функций, что и МТ.

Доказательство:

[math]\triangleright[/math]

Для того, чтобы доказать этот факт, докажем возможность построения всех возможных машин Тьюринга. В состав МТ входит: неограниченная в обе стороны лента, разделённая на ячейки управляющее устройство, способное находиться в одном из множества состояний. 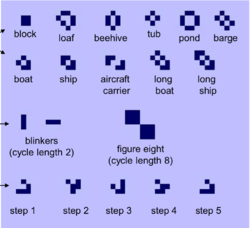Доказательство строится на том, что простая логика, необходимая для построения МТ, может быть построена в игре "Жизнь": детерминированный конечный автомат(с часами) ленту(с ячейками памяти) головку записи-чтения Базовые конструкции Рассмотрим базовые конструкции необходимые для построения этих элементов МТ. Glider gun Glider eater В игры "Жизнь" можно построить различные конструкции (см. рис.): стабильные — не меняются с течением времени(первые два ряда) циклические — принимают исходное положение каждые [math]n[/math] итераций (третий ряд) планер(glider) — фигура, которая смещается на одну клетку вниз и в право каждые [math]4[/math] итерации ([math]4[/math] ряд) космический корабль — фигура, которая смещается ортогонально на [math]1[/math] клетку каждые [math]4[/math] итерации glider gun — фигура, бесконечно производящая планер каждые [math]30[/math] итераций glider eater — фигура, поглощающая планеры 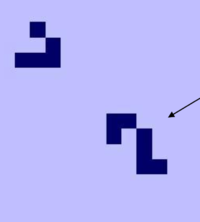Память Ячейки памяти можно построить с помощью стабильныx конструкций. Можно также построить c помощью планеров: наличие планера — [math]1[/math], отсутствие — [math]0[/math]. Часы В клеточных автоматах изначально есть часы, так как время увеличивается. Но в МТ необходимо, например, через определенное время передвигать головку записи, передавать информацию и пр. Для этой цели можно использовать планеры или космические корабли, так как они двигаются с известной скоростью. Следовательно, в качестве часов используем glider gun. Булевы функции Заметим, что управляющая часть МТ считывает с ленты входную строчку и завершается, записав на ленту выходную строчку. Без ограничения общности, будем рассматривать бинарные строки. Следовательно, управляющая часть МТ есть булева функция. Каждая МТ вычисляет определенную вычислимую функцию. Так как мы можем записать управляющий автомат в виде строки, можно подать МТ и входные данные на вход другой МТ. Следовательно, достаточно построить универсальную МТ. Если показать, что мы можем построить в игре "Жизнь" любую булеву функцию, то мы сможем построить булеву функцию УМТ. Из курса дискретной математики известно, что [math]NAND[/math] - полная система, т.е. с его помощью можно построить любую. Следовательно, чтобы построить любую булеву функцию, нам нужно просто построить [math]NAND[/math], то есть [math]NOT[/math] и [math]AND[/math] в игре "Жизнь". 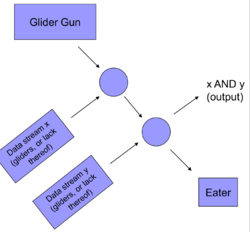Построение NOT Рассмотрим поток данных, состоящий из планеров. Наличие планера — [math]1[/math], отсутствие — [math]0[/math]. Добавим поток планеров, состоящий только из [math]1[/math]. При столкновении планеры исчезают, следовательно на месте [math]1[/math] образуется [math]0[/math] и наоборот. Построение AND См. рисунок. Пусть [math]AND(x, y)[/math], тогда y соударяется с [math]NOT(x)[/math]. Если [math]NOT(x) = 1[/math], то на выходе ничего не попадет, если [math]NOT( x) = 0[/math], то просто пройдет [math]y[/math].

[math]\triangleleft[/math]

Построение

Подробное описание построения МТ можно найти здесь: Rendell, P. (2014) Turing machine universality of the game of life. PhD, University of the West of England. Available from: http://eprints.uwe.ac.uk/22323