Уменьшение размерности

Под уменьшением размерности (англ. dimensionality reduction) в машинном обучении подразумевается уменьшение числа признаков датасета. Наличие в нем признаков избыточных, неинформативных или слабо информативных может понизить эффективность модели, а после такого преобразования она упрощается, и соответственно уменьшается размер набора данных в памяти и ускоряется работа алгоритмов ML на нем. Уменьшение размерности может быть осуществлено методами отбора признаков (англ. feature selection) или выделения признаков (англ. feature extraction).

Feature selection

Методы feature selection оставляют некоторое подмножество исходного набора признаков, избавляясь от признаков избыточных и слабо информативных. Основные преимущества этого класса алгоритмов:

• Уменьшение вероятности переобучения
• Увеличение точности предсказания модели
• Сокращение времени обучения
• Увеличивается семантическое понимание модели

Все методы отбора признаков можно разделить на 5 типов, которые отличаются алгоритмами выбора лишних признаков.

Filters

Фильтры (англ. filter methods) измеряют релевантность признаков на основе функции $\mu$, и затем решают по правилу $\kappa$, какие признаки оставить в результирующем множестве.

Фильтры могут быть:

• Одномерные (англ. univariate) — функция $\mu$ определяет релевантность одного признака по отношению к выходным меткам. В таком случае, обычно, измеряют "качество" каждого признака и удаляют худшие.
• Многомерные (англ. multivariate) — функция $\mu$ определяет релевантность некоторого подмножества исходного множества признаков относительно выходных меток.

Распространенными вариантами для $\mu$ являются:

• Коэффициент ранговой корреляции Спирмена (англ. Spearman's rank correlation coefficient) $=\displaystyle \frac{\sum_{i, j}(x_{ij}-\bar{x_j})(y_i-\bar{y})}{\sqrt{\sum_{i, j}(x_{ij}-\bar{x_j})^2\sum_i(y_i-\bar{y})^2}}$;
• Information gain $=\displaystyle -\sum_{i=1}^kp(c_i)\log_2{(p(c_i))}+\sum_{i=1}^{n}p(t_i)\sum_{j=1}^kp(c_j|t_i)log_2{(p(c_j|t_i))}$, и другие.

Преимуществом группы фильтров является простота вычисления релевантности признаков в датасете, но недостатком в таком подходе является игнорирование возможных зависимостей между признаками.

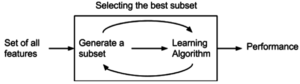
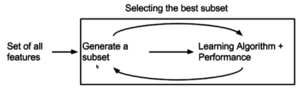
Wrappers

Процесс работы оберточных методов

Оберточные методы (англ. wrapper methods) находят подмножество искомых признаков последовательно, используя некоторый классификатор как источник оценки качества выбранных признаков, т.е. этот процесс является циклическим и продолжается до тех пор, пока не будут достигнуты заданные условия останова. Оберточные методы учитывают зависимости между признаками, что является преимуществом по сравнению с фильтрами, к тому же показывают большую точность, но вычисления занимают длительное время, и повышается риск переобучения.

Два самых простых типа оберточных методов:

• SFS (Sequential Forward Selection) — жадный алгоритм, который начинает с пустого множества признаков, на каждом шаге добавляя лучший из еще не выбранных признаков в результирующее множество
• SBS (Sequential Backward Selection) — алгоритм обратный SFS, который начинает с изначального множества признаков, и удаляет по одному или несколько худших признаков на каждом шаге

Популярным оберточным методом является SVM-RFE (SVM-based Recursive Feature Elimination), который иногда также обозначается как встроенный .

Embedded

Группа встроенных методов (англ. wrapper methods) очень похожа на оберточные методы, но для выбора признаков используется непосредственно структуру некоторого классификатора.

Процесс работы встроенных методов

Другие методы

Есть и другие методы отбора признаков: гибридные (англ. hybrid methods) и ансамблевые (англ. ensemble methods). Гибридные методы

См. также

• Переобучение
• SVM^{на 20.01.18 не создан}

Источники информации

1. Sequential feature selection — курс ML Texas A&M University
2. Feature selection — статья про Feature Selection в Wikipedia