Алгоритмы LZ77 и LZ78
и — алгоритмы сжатия без потерь, опубликованные Абрахамом Лемпелем[1] и Якобом Зивом[2] в и годах соответственно. Эти алгоритмы стали основой других алгоритмов семьи : LZW, LZSS, LZMA и другие. Оба приведенных алгоритма используют словарный подход.
Содержание
LZ77
Идея алгоритма
В кодируемых строках часто содержатся совпадающие длинные подстроки. Идея, лежащая в основе , заключается в замене повторений на ссылки на позиции в тексте, где такие подстроки уже встречались.
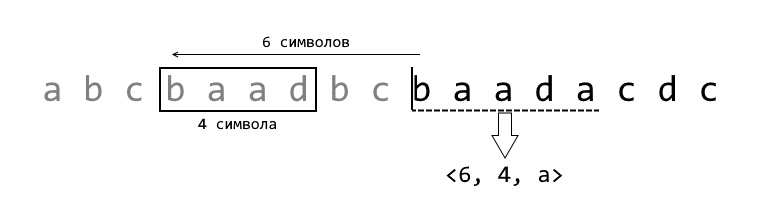
Информацию о повторении можно закодировать парой чисел — смещением назад от текущей позиции () и длиной совпадающей подстроки (). В таком случае, например, строка может быть представлена как . Выражение означает «вернись на символов назад и выведи символов».
Алгоритм кодирует ссылки блоками из трёх элементов — . В дополнение к двум уже описанным элементам, новый параметр означает первый символ после найденного совпадающего фрагмента. Если не удалось найти совпадение, то считается, что .
Для эффективного поиска повторов в применяется метод «скользящего окна» — совпадения ищутся не на всём обработанном префиксе, а в небольшом буфере, состоящем из последних обработанных символов. Обычно длина буфера равна , или . Таким образом, при больших объемах ввода алгоритм тратит меньше времени за счет того, что просматривается не вся исходная строка. С другой стороны, слишком маленькая длина словаря может привести к тому, что расположенные далеко друг от друга совпадения (на большем расстоянии, чем длина словаря) не будут учтены, и кодирование станет менее оптимальным.
Также нетривиальным может оказаться то, что при кодировании значение может быть меньше, чем (например, «вернись на символа назад и выведи символов»). Это означает, что подстрока будет повторяться несколько раз так, чтобы каждый символ совпадал с символом, стоящим на позиции раньше, и всего добавилось символов. Например: . Символ всегда можно определить однозначно, даже если он отсутствует в буфере.
Реализация
Хранить результат кодирования будем в списке структур следующего вида:
struct Node:
int offset
int length
char next
Функция findMatching ищет в буфере строку, совпадающую с префиксом суффикса строки , начинающегося с символа и возвращает искомую пару .
Функция shiftBuffer сдвигает буфер вперёд на символов.
// — исходная строка // функция возвращает список блоков list<Node> encodeLZ77(string s): list<Node> ans = [] pos = 0 while pos < s.length: offset, length = findMatching(buffer, pos) // ищем слово в словаре shiftBuffer(length + 1) // перемещаем скользящее окно pos += length ans.push({offset, length, s[pos]}) // добавляем в ответ очередной блок return ans
Пример
Рассмотрим пример кодирования на строке с буфером размера . Квадратом обведен буфер.
| Строка | Совпадение | Закодированная последовательность | Примечание |
|---|---|---|---|
| — | Буфер пуст | ||
| — | В буфере нет | ||
| Здесь выгодно сделать так, что | |||
| Последовательность уже встречалась, но она находится за пределами окна, и её не находит | |||
| Символов в строке больше нет, поэтому в качестве ставим символ конца строки |
Результатом кодирования является список полученных троек: .
Декодирование
Для декодирования необходимо пройти по уже раскодированной строке назад, вывести необходимую последовательность, затем следующий символ.
Псевдокод этого алгоритма:
// — список блоков // функция возвращает декодированную строку string decodeLZ77(list<Node> encoded): ans = "" for node in encoded: if node.length > 0: // если необходим повтор start = ans.length - node.offset // возвращаемся на символов назад for i = 0 .. node.length - 1: // добавляем символов ans += ans[start + i] ans += node.next // добавляем следующий символ return ans
Модификации
Известно много различных модификаций алгоритма . Например, вместо блоков можно хранить отдельно одиночные символы и отдельно — пары (length-distance pair[3]). Алгоритм LZSS является улучшением и хранит однобитный флаг, показывающий, какие данные за ним идут: одиночный символ или пара смещения и длины. В формате [4] на каждую пару смещения и длины выделяется по байта.
Также на основаны алгоритмы [5] и [6] (последний является широко используемым), которые совмещают с алгоритмом Хаффмана, кодируя элементы пар и одиночные символы.
LZ78
Идея алгоритма
Алгоритм имеет немного другую идею: этот алгоритм в явном виде использует словарный подход, генерируя временный словарь во время кодирования и декодирования.
Изначально словарь пуст, а алгоритм пытается закодировать первый символ. На каждой итерации мы пытаемся увеличить кодируемый префикс, пока такой префикс есть в словаре. Кодовые слова такого алгоритма будут состоять из двух частей — номера в словаре самого длинного найденного префикса () и символа, который идет за этим префиксом (). При этом после кодирования такой пары префикс с приписанным символом добавляется в словарь, а алгоритм продолжает кодирование со следующего символа.
Реализация
Будем хранить результат кодирования в такой структуре:
struct Node:
int pos // номер слова в словаре
char next
В качестве словаря будем использовать обычный map:
list<Node> encodeLZ78(string s):
string buffer = "" // текущий префикс
map<string, int> dict = {} // словарь
list<Node> ans = [] // ответ
for i = 0 .. s.length - 1:
if dict.hasKey(buffer + s[i]): // можем ли мы увеличить префикс
buffer += s[i]
else:
ans.push({dict[buffer], s[i]}) // добавляем пару в ответ
dict[buffer + s[i]] = dict.length + 1 // добавляем слово в словарь
buffer = "" // сбрасываем буфер
if not (buffer is empty): // если буффер не пуст - этот код уже был, нужно его добавить в конец словаря
last_ch = buffer.peek() // берем последний символ буффера, как "новый" символ
buffer.pop() // удаляем последний символ из буфера
ans.push({dict[buffer], last_ch}) // добавляем пару в ответ
return ans
Пример
В этот раз для примера возьмем строку .
| Словарь | Осталось обработать | Найденный префикс | Код | Примечание |
|---|---|---|---|---|
| — | В словаре ничего не нашлось, вместо номера в словаре указываем | |||
| — | ||||
| , | Нашелся префикс (слова в словаре нумеруются с ), добавляем | |||
| , , | ||||
| , , , | ||||
| , , , , | — | |||
| , , , , , |
Результатом кодирования является список пар:
Декодирование
Декодирование происходит аналогично кодированию, на основе декодируемой информации строим словарь и берем из него значения.
string decodeLZ78(list<Node> encoded):
list<string> dict = [""] // словарь, слово с номером 0 — пустая строка
string ans = "" // ответ
for node in encoded:
word = dict[node.pos] + node.next // составляем слово из уже известного из словаря и новой буквы
ans += word // приписываем к ответу
dict.push(word) // добавляем в словарь
return ans
Модификации
Одна из главных проблем — размер словаря. Он ничем не ограничен и может достигать огромных размеров на больших объемах входных данных. В различных модификациях установлены лимиты на размер словаря: при достижении определенного лимита словарь может «замораживаться» (в него перестают добавляться новые слова), из словаря могут удалять менее используемые или самые старые слова и так далее.
Самой известной модификацией является LZW. В нём есть две важных особенности. Первая — словарь изначально инициализирован всеми символами алфавита. Вторая — после нахождения максимального префикса поиск следующего префикса начинается не с символа после неподходящего, а с самого неподходящего символа. Это позволяет не выводить неподходящий символ, а выяснять его прямо из словаря. Эта модификация используется в том числе в изображениях в формате [7].