Многомерное дерево Фенвика
| Определение: |
Многомерное дерево Фенвика (англ. Multidimensional Binary Indexed Tree) — структура данных, требующая памяти и позволяющая эффективно (за )
|
Рассмотрим для начала дерево Фенвика на примере k-мерного массива с , а затем посмотрим, как можно обобщить его на большие размерности.
Пусть дан массив из элементов: .
Деревом Фенвика будем называть массив из элементов: , где , как и в одномерном дереве Фенвика.
Содержание
Пример задачи для двумерного случая
Пусть имеем набор точек на плоскости с неотрицательными координатами. Определены 3 операции:
- добавить точку в ;
- удалить точку из ;
- посчитать количество точек в прямоугольнике ;
— количество точек, — максимальная координата, — максимальная координата.
Тогда дерево строится за , а запросы выполняются за
Добавляя точку вызовем , а удаляя . Таким образом запрос дает количество точек в прямоугольнике.
Псевдокод
— массив, в котором хранится дерево Фенвика.
int sum(x: int, y: int):
int result = 0
for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
for (int j = y; j >= 0; j = (j & (j + 1)) - 1)
result += t[i][j];
return result;
func inc(x: int, y: int, delta: int):
for (int i = x; i < maxX; i = (i | (i + 1)))
for (int j = y; j < maxY; j = (j | (j + 1)))
t[i][j] += delta;
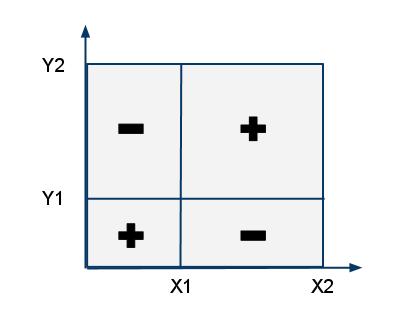
Чтобы посчитать значение функции для прямоугольника нужно воспользоваться формулой включения-исключения. Например, для суммы:
Обобщение на большие размерности
Дерево Фенвика относится к структурам данных, требующим малое количество дополнительной памяти. В комбинации с простым представлением тривиального случая данной структуры это дает возможность легко повышать размерность дерева Фенвика, в котором в ячейках какого-то фиксированного уровня будет находиться дерево меньшей размерности. Для его реализации нам достаточно во всех операциях для каждой новой размерности просто добавить вложенный цикл, пробегающий в ней соответствующие индексы.