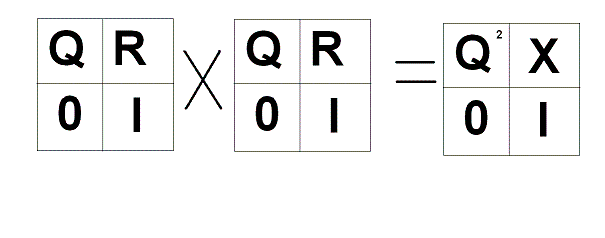Теорема о поглощении
Формулировка теоремы
Формулировка
С вероятностью, равной 1, марковская цепь перейдет в поглощающее состояние, если у нее существует такое состояние.
Доказательство теоремы
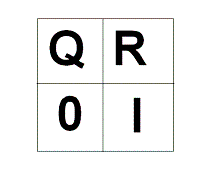
Пусть P - матрица переходов, где элемент равен вероятности перехода из i-го состояния в j-ое. Она будет выглядеть как матрица из 4-х блоков, где Q - несущественные состояния, а R и I - существенные.(т.к. цепь поглощающая, то из любого несущественного можно попасть в существенное) I - единичная матрица.
Пусть вектор - вектор вероятности нахождения на шаге t. Он вычисляется, как произведение вектора на нулевом шаге на матрицу перехода в степени t. Рассмотрим, что представляет из себя возведение матрицы P в степень:
Отсюда видно, что имеет такой вид, где X - некоторые значения.
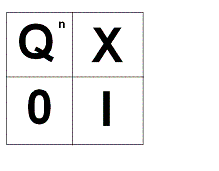
Следовательно нам надо доказать, что , при
Рассмотрим путь из i-го состояния в поглощающее, равное . Пусть - вероятность того, что через шагов из шага i не попадет в поглощающее состояние. Пусть , а
Тогда получаем:
В итоге получаем, что несущественные состояния стремятся к 0, а значит существенные в итоге приходят к 1, т.е. цепь приходит в поглощающее состояние.