Укладка дерева

Дерево — планарный граф. Его планарность можно подтвердить, предъявив способ укладки для произвольного дерева или же, воспользовавшись теоремой Понтрягина-Куратовского, заметить, что раз этот граф по определению не содержит циклов, значит и подграфов, гомеоморфных [math]K_{5}[/math] или [math]K_{3, 3}[/math] содержать не может, а значит он планарен. По формуле Эйлера [math]V - E + F = 2, V - (V - 1) + F = 2 \Leftrightarrow F = 1 [/math].

Укладка дерева

Рисунок 1. Пример поуровневой укладки дерева.

Существуют несколько способов укладки дерева на плоскости.

Поуровневая укладка

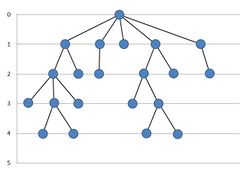
Простой способ построения нисходящего плоского изображения дерева заключается в использовании его поуровневого расположения (layered drawing), при котором вершины глубины [math]a[/math] имеют координату [math]y = – a[/math], а координаты по горизонтальной оси распределяются так, чтобы никакие левые поддеревья не пересекались с правыми. Возможна реализация за линейное время, позволяющая получить оптимальное по ширине плоское дерево в области размера [math]O(N^2)[/math] (где [math]N[/math] — число вершин дерева).

Радиальная поуровневая укладка

Рисунок 2. Граф из рисунка 1, но уложенный радиально.

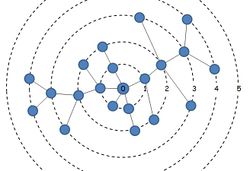
Радиальная поуровневая укладка(radial drawing) дерева отличается тем, что его уровни имеют вид концентрических окружностей, поддеревья занимают секторные сегменты.

Выбор угла [math]\beta_p[/math] секторного сегмента для поддерева с корнем [math]p[/math] и количеством вершин [math]l(p)[/math] определяется следующим образом: пусть вершина [math]p[/math] лежит на уровне [math]C_i[/math], тогда для каждого ее сына [math]q[/math] имеем: [math]\beta_q = \min(\frac{l(q)\beta_p}{l(p)}, \tau)[/math], где [math]\tau[/math] — это угол области [math]F_p[/math], определяемой пересечением касательной к точке [math]p[/math] уровня [math]C_i[/math] и окружностью уровня [math]C_{i+1}[/math].

Радиальное изображение дерева часто используют для представления свободных деревьев, причем в качестве вершины, размещаемой в центре, берется одна из его центральных вершин.

Рисунок 3. Пример укладки двоичного дереве в виде hv-изображения.

hv-изображения

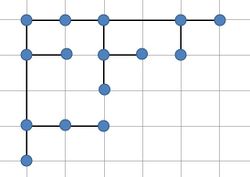
Бинарные деревья можно изобразить при помощи hv-изображений (horizontal-vertical drawing). При этом для каждой вершины [math]p[/math] выполняются следующие свойства:

• сын вершины [math]p[/math] ставится в ряд за [math]p[/math] либо по горизонтали справа, либо по вертикали вниз
• два прямоугольника, ограничивающие левое и правое поддерево вершины [math]p[/math] не пересекаются

Ссылки

• Tree Drawing Algorithms and Tree Visualisation Methods (PDF)