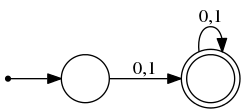
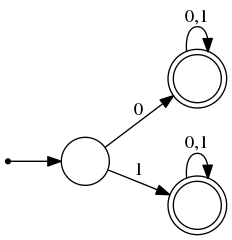
Эквивалентность состояний ДКА

Определение:

Два автомата [math] \mathcal{A}_1 = \langle Q_1,\Sigma,\delta_1,s_{1}, T_1\subseteq Q_1 \rangle [/math] и [math]\mathcal{A}_2 = \langle Q_2,\Sigma,\delta_2,s_{2}, T_2\subseteq Q_2 \rangle [/math] называются эквивалентными, если они распознают один и тот же язык над алфавитом [math]\Sigma[/math], то есть [math]\mathcal{L}(\mathcal{A}_1) = \mathcal{L}(\mathcal{A}_2)[/math].

Определение:

Слово [math]z \in \Sigma^*[/math] различает два состояния [math]q_i[/math] и [math]q_j[/math], если [math] \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow t_1 \notin T \Leftrightarrow t_2 \in T [/math].

Определение:

Два состояния [math]q_i[/math] и [math]q_j[/math] называются эквивалентными [math](q_i \sim q_j)[/math], если не существует строки, которая их различает, то есть [math]\forall z \in \Sigma^*[/math] верно, что [math] \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow t_1 \in T \Leftrightarrow t_2 \in T [/math].

Заметим, что эквивалентность состояний действительно является отношением эквивалентности. Так как [math] \Leftrightarrow [/math] (равносильность) является отношением эквивалентности и [math] \forall z \in \Sigma^*\ \forall q \in Q \ \exists ! t : \langle q, z \rangle \vdash^* \langle t, \varepsilon \rangle [/math], поэтому описанное нами отношение является отношением эквивалентности.

Пример

Эти два автомата принимают слова из языка слов длины не меньше одного, состоящих из символов алфавита [math] \lbrace 0, 1\rbrace [/math]. Все допускающие состояния автоматов эквивалентны между собой.

Лемма:

[math] \mathcal{A} = \langle Q, \Sigma, \delta, s, T \rangle [/math], [math] p_1, p_2, q_1, q_2 \in Q [/math], [math] q_i = \delta(p_i, c) [/math], [math] w \in \Sigma^*[/math] различает [math] q_1 [/math] и [math] q_2 [/math]. Тогда [math]cw[/math] различает [math] p_1 [/math] и [math] p_2 [/math].

Доказательство:

[math]\triangleright[/math]

[math] \langle p_i, cw \rangle \vdash \langle q_i, w \rangle \vdash^* \langle t_i, \varepsilon \rangle [/math] А значит, по условию различимости для [math] q_1 [/math] и [math] q_2[/math] , [math] t_1 \in T \Leftrightarrow t_2 \notin T [/math]

[math]\triangleleft[/math]

Алгоритм проверки эквивалентности автоматов

Постановка задачи

Даны два детерминированных конечных автомата [math] \mathcal{A}_1 = \langle Q_1,\Sigma,\delta_1,s_{1}, T_1\subseteq Q_1 \rangle [/math] и [math]\mathcal{A}_2 = \langle Q_2,\Sigma,\delta_2,s_{2}, T_2\subseteq Q_2 \rangle [/math]. Требуется определить, эквивалентны ли они.

Алгоритм

Рассмотрим такие семейства множеств:

• [math] D_i = \lbrace \langle q, p\rangle | q \in Q_1, p \in Q_2, \exists w : |w| \le i, w [/math] различает [math] q [/math] и [math] p \rbrace [/math];
• [math] E_i = D_i \setminus D_{i - 1} [/math].

Для [math] D_i [/math] существует рекуррентная формула:

• [math] D_i = D_{i - 1} \cup \lbrace \langle p, q \rangle | \exists c \in \Sigma : \langle \delta(p, c), \delta(q, c) \rangle \in E_{i - 1} \rbrace [/math].

То есть [math] D_i [/math] — объединение множества всех пар состояний, которые различаются строками длины меньшей [math] i [/math] с множеством всех пар состояний, которые различаются строками длины ровно [math]i[/math].

Заметим, что [math] \exists k : E_k = \varnothing [/math], причем [math] k \le |Q| ^ 2[/math]. Также заметим, что [math] E_k = \varnothing \Rightarrow E_{k + 1} = \varnothing [/math], так как в [math] D_{k+1}[/math] новых элементов не добавится, поэтому [math] D_{k+1} = D_k [/math]. Значит:

• [math] E_k = \varnothing \Rightarrow D_k = \lbrace \langle q, p\rangle | q \in Q_1, p \in Q_2, \exists w : w [/math] различает [math] q [/math] и [math] p \rbrace = \lbrace \langle q, p\rangle | (q \nsim p)\rbrace[/math].

Осталось найти такое [math] k [/math] и [math] D_k [/math], что [math] E_k = \varnothing [/math] тогда мы узнаем пары неэквивалентных состояний, останется только проверить, что [math] \langle s_1, s_2 \rangle \notin D_k [/math], тогда автоматы будут эквивалентны.

Будем строить [math] D_i [/math] в порядке увеличения [math] i [/math], пока [math] D_i \neq D_{i - 1}[/math]. Заметим, что [math] D_0 = \lbrace \langle p, q\rangle | p \in T_1 \Leftrightarrow q \notin T_2 \rbrace [/math], так как строка длины 0 одна — это [math] \varepsilon [/math], а [math] \varepsilon [/math] различает только пары состоящие из одного терминального состояния и одного нетерминального.

Дальше будем получать [math] D_i [/math] по рекуррентной формуле, пока не выполнится условие остановки.

Это можно реализовать проще: будем хранить для каждого состояния, из какого состояния есть переход по символу [math] c [/math] в наше. В очередь будем класть пары неэквивалентных состояний. Дальше вытаскивая из очереди пару, рассмотрим все пары состояний, из которых есть переход по одинаковому символу в элементы пары из очереди. Пометим их неэквивалентными и положим в очередь.

Псевдокод

   [math] q = \varnothing [/math]
   fill(neq, false)
   for [math] p_1 \in Q_1 [/math]
       for [math] p_2 \in Q_2 [/math]
           if [math] (p_1 \in T_1) \neq (p_2 \in T_2) [/math]
               q.push([math]p_1[/math],[math] p_2[/math])
               neq[[math]p_1[/math], [math]p_2[/math]] = True
   while not isEmpty(q)
       [math] \langle p_1, p_2 \rangle [/math] = q.pop()
       for [math] c \in \Sigma [/math]
           for [math] \delta(e_1, c) = p_1 [/math]
               for [math] \delta(e_2, c) = p_2 [/math]
                   q.push([math]e_1[/math], [math]e_2[/math])
                   neq[[math]e_1[/math], [math]e_2[/math]] = True
   if neq[[math]s_1[/math], [math]s_2[/math]]
       print("Not equivalent")
   else
       print("Equivalent")

Время работы алгоритма

Алгоритм будет работать за [math] O(|Q_1||Q_2||\Sigma|^2)[/math].