Идеальное хеширование
Двойное хеширование (double hashing) - один из методов закрытого хеширования. Перебор ячеек хеш-таблицы, возникающий при двойном хешировании, обладает свойствами, присущими равномерному хешированию. При двойном хешировании хеш-функция имеет следующий вид:
где и - вспомогательные хеш-функции, - размер хеш-таблицы. Иными словами, последовательность индексов исследуемых ячеек при работе с ключом представляет собой арифметическую прогрессию (по модулю ) с первым членом и шагом . Следовательно, в данном случае последовательность исследования зависит от ключа k по двум параметрам - выбор начальной исследуемой ячейки и расстояние между двумя исследуемыми ячейками, так как оба параметра зависят от значения ключа.
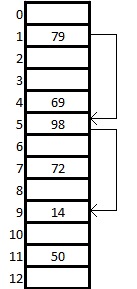
Пример вставки элемента при двойном хешировании приведен на рисунке справа.
Показана хеш-таблица размером 13 ячеек, в которой используются вспомогательные функции:
Мы хотим вставить ключ 14. Изначально . Тогда . Но ячейка с индексом 1 занята, поэтому увеличиваем на 1 и пересчитываем значение хеш-функции. Делаем так, пока не дойдем до пустой ячейки. При получаем . Ячейка с номером 9 свободна, значит записываем туда наш ключ.
Для того, чтобы последовательность исследования могла охватить всю таблицу, значение должно быть взаимно простым с размером таблицы. Есть два удобных способа это сделать. Первый состоит в том, что в качестве размера таблицы используется простое число, а возвращает натуральные числа, меньшие . Второй - размер таблицы является степенью двойки, а возвращает нечетные значения.
Таким образом, основная особенность двойного хеширования состоит в том, что при различных пара дает различные последовательности ячеек для исследования.
Простая реализация
Вставка
insert(item){
x = h1(item.key)
y = h2(item.key)
for (i = 0; i < m; i++){
if (table[x] == null){
table[x] = item
return
}
x = (x + y) % m
}
error() //ошибка, требуется увеличить размер таблицы
}
Поиск
search(key){
x = h1(key)
y = h2(key)
for (i = 0; i < m; i++){
if (table[x] != null)
if (table[x].key == key)
return table[x]
else
return null
x = (x + y) % m
}
return null
}
Реализация с удалением
Вставка
insert(item){
x = h1(item.key)
y = h2(item.key)
for (i = 0; i < m; i++){
if (table[x] == null || deleted[x]){
table[x] = item
deleted[x] = false
return
}
x = (x + y) % m
}
error() //ошибка, требуется увеличить размер таблицы
}
Поиск
search(key){
x = h1(key)
y = h2(key)
for (i = 0; i < m; i++){
if (table[x] != null)
if (table[x].key == key && !deleted[x])
return table[x]
else
return null
x = (x + y) % m
}
return null
}
Удаление
remove(key){
x = h1(key)
y = h2(key)
for (i = 0; i < m; i++){
if (table[x] != null)
if (table[x].key == key)
deleted[x] = true
else
return
x = (x + y) % m
}
}
См. также
Литература
- Бакнелл Дж. М. Фундаментальные алгоритмы и структуры данных в Delphi, 2003
- Кнут Д. Э. Искусство программирования, том 3. Сортировка и поиск, 2-е издание, 2000
- Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы. Построение и анализ, 2010
- Седжвик Р. Фундаментальные алгоритмы на C. Части 1-4. Анализ. Структуры данных. Сортировка. Поиск, 2003