Материал из Викиконспекты
Эта статья находится в разработке!
Рассмотрим задачу:
- Дано [math]n[/math] работ и [math]2[/math] станка.
- Для каждой работы известно её время выполнения на каждом станке.
Требуется минимизировать время окончания всех работ, если каждую работу необходимо выполнить на обоих станках.
Описание алгоритма
Пусть [math]a_{i}[/math] — время выполнения [math]i[/math]-ой работы на первом станке, а [math]b_{i}[/math] — на втором.
- Разобьём все работы на два множества: [math]I = \{i \mid a_{i} \le b_{i}; i = 1, \dots, n\}[/math] и [math]J = \{i \mid a_{i} \gt b_{i}; i = 1, \dots, n\}[/math]
- Найдем [math]a_{x} = \max \{a_{i} \mid i \in I\}[/math] и [math]b_{y} = \max \{b_{i} \mid i \in J\}[/math]
- Рассмотрим 2 случая. Первый случай, когда [math]a_{x} \ge b_{y}[/math], тогда
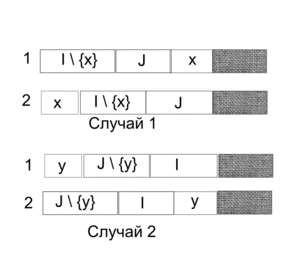
- Выполняем все работы на первом станке в следующем порядке: сперва все работы из [math]I \setminus \{x\}[/math], затем из [math]J[/math] и последней работу [math]x[/math]
- На втором станке выполняем первой работу [math]x[/math]
- Остальные работы выполняем на втором станке в порядке их завершения на первом тогда, когда второй станок свободен, а работа на первом уже выполнена
Второй случай рассматривается аналогично: первый и второй станок меняются местами, и вместо [math]x[/math] — работа [math]y[/math]
Псевдокод
[math]I \leftarrow \varnothing [/math]
[math]J \leftarrow \varnothing [/math]
for [math]i = 1 \dots n[/math]
if [math]a_{i} \le b{i}[/math]
[math] I \leftarrow I \cup \{i\} [/math]
else
[math] J \leftarrow J \cup \{i\} [/math]
Найти [math]x[/math], где [math]a_{x} = \max \limits_{i \in I} \{a_{i}\}[/math]
Найти [math]y[/math], где [math]b_{y} = \max \limits_{i \in J} \{b_{i}\}[/math]
if [math]a_{x} \lt b_{y}[/math]
Поменять местами первый и второй станок
Пересчитать [math]I, J, x[/math]
Запомнить, что поменяли
[math]time1 \leftarrow 0[/math]
shed2[x] [math]\leftarrow 0[/math]
[math]time2 \leftarrow b_{x}[/math]
Для всех [math]i \in I \setminus \{x\}[/math]
sched1[i] [math]\leftarrow time1[/math]
[math]time1 \leftarrow time1 + a_{i}[/math]
[math]time2 \leftarrow \max\{time1, time2\}[/math]
sched2[i] [math]\leftarrow time2[/math]
[math]time2 \leftarrow time2 + b_{i}[/math]
Для всех [math]i \in J[/math]
sched1[i] [math]\leftarrow time1[/math]
[math]time1 \leftarrow time1 + a_{i}[/math]
[math]time2 \leftarrow \max\{time1, time2\}[/math]
sched2[i] [math]\leftarrow time2[/math]
[math]time2 \leftarrow time2 + b_{i}[/math]
[math]time1 \leftarrow \max\{time1, b_{x}\}[/math]
sched1[x] [math]\leftarrow time1[/math]
[math]time1 \leftarrow time1 + a_{x}[/math]
[math]C_{max} \leftarrow \max\{time1, time2\}[/math]
if станки меняли местами
поменять их обратно
Сложность алгоритма
Каждое из множеств в сумме содержит [math]n[/math] элементов. Следовательно, чтобы найти максимум в каждом из множеств нам потребуется [math]O(n)[/math] операций, чтобы составить расписание для каждой работы из множества нам потребуется так же [math]O(n)[/math] операций. Получаем сложность алгоритма [math]O(n)[/math].