Персистентная приоритетная очередь
Персистентная приоритетная очередь (англ. persistent priority queue) - это приоритетная очередь, реализующая персистентность, то есть позволяющая получить доступ ко всем своим предыдущим версиям.
Основная идея
Возьмем биномиальную кучу и реализуем ее на односвязных списках.
Для этого будем хранить список корней в порядке возрастания ранга, а детей будем хранить по убыванию ранга. Каждый родитель будет знать ребенка с большим рангом, который является головой списка детей, но ребенок не будет знать родителя.
Операции
Merge
Проходим по корневым спискам и создаем новый, объединяя деревья одинакового ранга.
merge_tree(t1, t2)
if (t1.key < t2.key)
t2.next = t1.son;
t1.son = t2;
else
t1.next = t2.son;
t2.son = t1;
Проход по корневым спискам выполнится за , объединение деревьев выполняется за . Тогда работает за .
Insert
Разрешим при объединении двух деревьев присоединять еще одну вершину, дерево ранга 0. Тогда получится возможным существование еще двух типов деревьев:
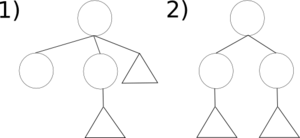
Разберем случаи добавления.
а) Минимальный ранг дерева и такое дерево одно. Добавим новое дерево ранга 0 - нашу вершину.
б) Минимальный ранг дерева и таких деревьев два. Объединим эти деревья и нашу вершину в дерево ранга , получим дерево типа 1 или 2 в зависимости от того у какой вершины ключ меньше.
Тогда работает за .
extractMinimum
Работает так же как и в обычной биномиальной куче. Проходим по списку корней и находим вершину с минимальным ключом.
extractMinimum(t)
t1=t;
while t1.next != null
if min.val>t1.val
min = t1;
t1 = t1.next;
par = t;
t1 = t;
while min != t1
par = t1;
t1 = t1.next;
par.next = par.next.next;
return (min, t)
Возвращает дерево с минимальным элементом и остаток от очереди после извлечения минимума. Работает за .