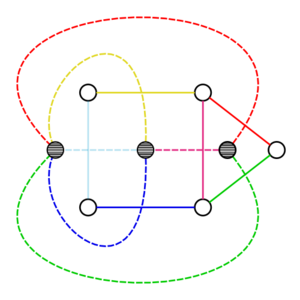
Двойственный граф планарного графа
| Определение: |
Граф G′ называется двойственным к планарному графу G, если:
|
«…Для данного плоского графа G его двойственный граф G′ строится следующим образом: поместим в каждую область G (включая внешнюю) по одной вершине графа G′ и, если две области имеют общее ребро x, соединим помещенные в них вершины ребром x′, пересекающим только x. В результате всегда получится плоский псевдограф. Ясно, что G′ имеет петлю тогда и только тогда, когда в G есть концевая вершина; G′ имеет кратные рёбра тогда и только тогда, когда две области графа G содержат по крайней мере два общих ребра. Таким образом, двусвязный плоский граф имеет всегда в качестве двойственного или граф или мультиграф, в то время как двойственный граф трёхсвязного плоского графа всегда представляет собой граф. Другими примерами двойственных графов являются платоновы графы: тетраэдр — самодвойственный граф, куб и октаэдр — двойственные, так же как додекаэдр и икосаэдр…»[1].
Свойства
- На самом деле, двойственный граф — мультиграф, поскольку в нём могут быть петли и кратные рёбра
- Если G′ — двойственный к двусвязному графу G, то G — двойственный к G′
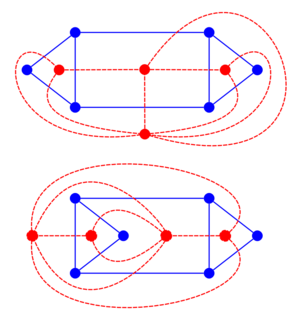
- У одного и того же графа может быть несколько двойственных, в зависимости от конкретной укладки (см. картинку)
Примечания
- ↑ Харари, Ф. Теория графов. —М.: Книжный дом «ЛИБРОКОМ», 2009. — С. 138. — ISBN 978-5-397-00622-4