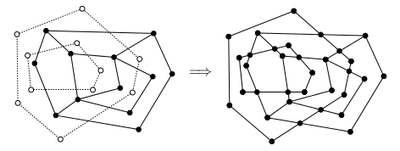
Пересечение многоугольников (PSLG overlaying)
Алгоритм
MapOverlay (, )
Дано: 2 ППЛГ в виде РСДС.
Вывод: пересечение этих ППЛГ в виде РСДС. Алгоритм:
1. Копируем и в РСДС .
2. Находим все пересечения ребер из с ребрами из с помощью заметающей прямой.
2.1 Когда находим точки пересечения, то обновляем .
3. Теперь это нормальный РСДС, но без информации о faces.
4. Находим boundary cycles в .
5. Создаем граф , в котором узлы будут отвечать за boundary cycles и в котором ребра будут соединять только те узлы, один из которых будет являться границей дыры, а другой будет находиться слева от самой левой точки первого. (В случае, если это самая внешняя граница, то для нее пусть будет мнимая гигантская граница, с которой мы ее и соединим).
6. Для каждой компоненты графа:
7. Пусть будет уникальная наружная граница цикла в компоненте, а будет означать face ограниченный этим циклом. Создадим face для . Запишем outer_component в какой-нибудь half-edge из . И создадим список inner_components, состоящий из указателей на какой-нибудь half-edge из каждого цикла. А так же пусть incident_face в каждом half-edge будут обновлены на .
Q&A
- Копирование РСДС
Просто объединение в одну структуру. Как сделать его правильным - это уже следующие пункты.
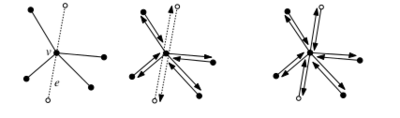
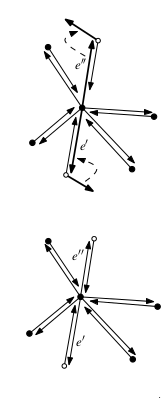
- Как из пересечения ребер сделать новую компоненту РСДС
См рисунок.
- Сколько будет faces?
Столько же, сколько outer boudaries + 1.
- Как узнать, что данный цикл это внешняя граница для face или же это дыра в нем?
Мы знаем, что face находится слева от half-edge. Поэтому возьмем самую левую точку (в случаем, если их несколько, то самую нижнюю) и возьмем входящий и выходящий из нее half-edge. В случае угла между ними менее 180 градусов, то это внешняя граница, иначе это дыра. Это действует только для самой левой точки из цикла.
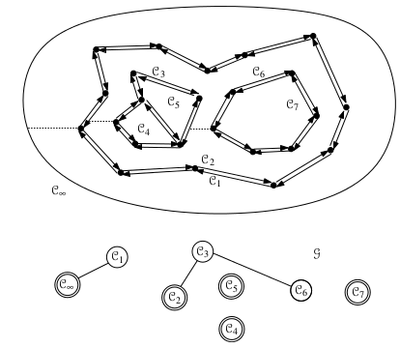
- Че за граф такой пацанский?
См рисунок. Из него мы сможем понять, какие циклы принадлежат одному и тому же face. Например, в рисунке мы видим, что C2, C3 и C6 являются циклами одного face. Из предыдущего вопроса мы понимаем, что C2 есть внешняя граница.
| Лемма: |
Каждая компонента графа отвечает за множество циклов инцидентных одному face. |
| Доказательство: |
| Рассмотрим цикл , который ограничивает дыру в face . Поскольку локально лежит левее самой левой вершины из , то должен быть соединен с другим циклом, который тоже ограничивает . отсюда следует, что циклы есть компонента связности в графе, описывающая один и тот-же face. Для того, что бы закончить доказательство, покажем, что каждый цикл ограничивающий дыру в есть в той же компоненте связности, что и внешняя граница . Предположим, что есть цикл, для которого это не так. Пусть — самый левый такой цикл, то есть тот, чья самая левая вершина самая левая (шляпа). По определению есть ребро между и неким , который лежит слева от самой левой вершины . Следовательно в той же компоненте связности, что и , который не в той же компоненте, что внешняя граница . Противоречие. |
- Как построить этот граф?
Вспоминаем, что во время работы алгоритма заметающей прямой, мы смотрели на отрезки левее от event point. Из этого получаем, что информацию для постройки нашего графа мы получаем из этого алгоритма. То есть для начала мы делаем узел для каждого цикла, затем для создания ребер мы смотри на самые левые вершины циклов. Если есть half-edge слева от вершины, то создаем ребро между циклами (в котором вершина и в котором half-edge).
- Еще что-то?
Да. названия face должны быть такими-же как в старых РСДС. (Как это делать. Много букв и много не нужного, но пусть будет. Легко перевести) One thing remains: each face f in the overlay must be labeled with the names of the faces in the old subdivisions that contained it. To find these faces, consider an arbitrary vertex v of f . If v is the intersection of an edge e 1 from S 1 and an edge e 2 from S 2 then we can decide which faces of S 1 and S 2 contain f by looking at the IncidentFace() pointer of the appropriate half-edges corresponding to e 1 and e 2 . If v is not an intersection but a vertex of, say, S 1 , then we only know the face of S 1 containing f . To find the face of S 2 containing f , we have to do some more work: we have to determine the face of S 2 that contains v. In other words, if we knew for each vertex of S 1 in which face of S 2 it lay, and vice versa, then we could label the faces of O(S 1 , S 2 ) correctly. How can we compute this information? The solution is to apply the paradigm that has been introduced in this chapter, plane sweep, once more. However, we won’t explain this final step here. It is a good exercise to test your understanding of the plane sweep approach to design the algorithm yourself. (In fact, it is not necessary to compute this information in a separate plane sweep. It can also be done in the sweep that computes the intersections.)
Литература и источники
- Вычислительная геометрия. Алгоритмы и приложения, де Берг Марк и другие. Глава 2.3