Алгоритм Прима

Алгоритм Прима(англ. Prim's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе.

Идея

Данный алгоритм очень похож на алгоритм Дейкстры. Будем последовательно строить поддерево [math]F[/math] ответа в графе [math]G[/math], поддерживая приоритетную очередь [math]Q[/math] из вершин [math]G \setminus F[/math], в которой ключом для вершины [math]v[/math] является [math]\min\limits_{u \in V(F), uv \in E(G)}w(uv)[/math] — вес минимального ребра из вершин [math]F[/math] в вершину [math]v[/math]. Также для каждой вершины очереди будем хранить [math]p(v)[/math] — вершину [math]u[/math], на которой достигается минимум в определении ключа. Дерево [math]F[/math] поддерживается неявно, и его ребра — это пары [math]\left(v,p(v)\right)[/math], где [math]v \in G \setminus \{r\} \setminus Q[/math], а [math]r[/math] — корень [math]F[/math]. Изначально [math]F[/math] пусто и значения ключей у всех вершин равны [math]+\infty[/math]. Выберём произвольную вершину [math]r[/math] и присвоим её ключу значение [math]0[/math]. На каждом шаге будем извлекать минимальную вершину [math]v[/math] из приоритетной очереди и релаксировать все ребра [math]vu[/math], такие что [math]u \in Q[/math], выполняя при этом операцию [math]\text{decreaseKey}[/math] над очередью и обновление [math]p(v)[/math]. Ребро [math]\left(v,p(v)\right)[/math] при этом добавляется к ответу.

Реализация

function Prim(G, w)
   for каждой вершины v из графа G
       key[v] = [math]\infty[/math]
       p[v] = NIL
   r = произвольная вершина графа G
   key[r] = 0 
   Q.push(все вершины графа G) 
   while Q не пуста
       v = extractMin(Q) 
       for всех u смежных с v
           if u in Q and key[u] > w(v, u)
               p[u] = v
               key[u] = w(v, u)
               Q.decreaseKey(u, key[u])

Ребра дерева восстанавливаются из его неявного вида после выполнения алгоритма.
Операцию [math]decreaseKey[/math] сделать для приоритетной очереди на двоичной куче немного проблематично, поэтому есть два варианта. Первый, написать приоритетную очередь на какой-то сложной куче, например, биноминальной или фибоначчиевой. Второй, изменять значение ключа вершины, для которой вызвали [math]decreaseKey[/math], непосредственно в куче, после чего делать процедуру просеивания вверх для этой вершины. Для быстрого доступа к позиции вершины в куче, нужно дополнительно хранить указатель на эту позицию и не забывать его менять во время изменения кучи.

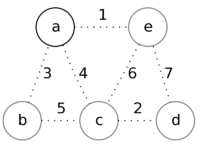
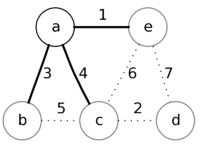
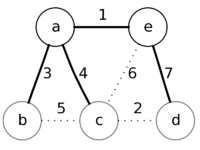
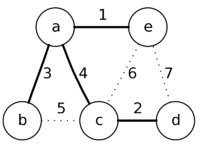
Пример

Рассмотрим работу алгоритма на примере графа. Пусть произвольно выбранная вершина — это вершина a.

Изображение	Множество вершин	Описание
	a b c d e [math] 0 [/math] [math]\infty[/math] [math]\infty[/math] [math]\infty[/math] [math]\infty[/math]	Извлечём из множества вершину a, так как её приоритет минимален. Рассмотрим смежные с ней вершины b, c, и e. Обновим их приоритеты, как веса соответствующих рёбер ab, ac и ae, которые будут добавленны в ответ.
	a b c d e [math] 0 [/math] [math] 3 [/math] [math] 4 [/math] [math]\infty[/math] [math] 1 [/math]	Теперь минимальный приоритет у вершины е. Извлечём её и рассмотрим смежные с ней вершины a, c, и d. Изменим приоритет только у вершины d, так как приоритеты вершин a и с меньше, чем веса у соответствующих рёбер ea и ec, и установим приоритет вершины d равный весу ребра ed, которое будет добавленно в ответ.
	a b c d e [math] 0 [/math] [math] 3 [/math] [math] 4 [/math] [math] 7 [/math] [math] 1 [/math]	После извлечения вершины b ничего не изменится, так как приоритеты вершин a и с меньше, чем веса у соответствующих рёбер ba и bc. Однако, после извлечения следующей вершины - c, будет обновлён приоритет у вершины d на более низкий (равный весу ребра cd) и в ответе ребро ed будет заменено на cd.
	a b c d e [math] 0 [/math] [math] 3 [/math] [math] 4 [/math] [math] 2 [/math] [math] 1 [/math]	Далее будет рассмотрена следующая вершина - d, но ничего не изменится, так как приоритеты вершин e и с меньше, чем веса у соответствующих рёбер de и dc. После этого алгоритм завершит работу, так как в заданном множестве не останется вершин, которые не были бы рассмотрены

Корректность

По поддерживаемым инвариантам после извлечения вершины [math]v[/math] ([math]v \neq r[/math]) из [math]Q[/math] ребро [math]\left(v,p(v)\right)[/math] является ребром минимального веса, пересекающим разрез [math]\left(F,Q\right)[/math]. Значит, по лемме о безопасном ребре, оно безопасно. Алгоритм построения MST, добавляющий безопасные ребра, причём делающий это ровно [math]|V|-1[/math] раз, корректен.

Оценка производительности

Производительность алгоритма Прима зависит от выбранной реализации приоритетной очереди, как и в алгоритме Дейкстры. Извлечение минимума выполняется [math]V[/math] раз, релаксация — [math]O(E)[/math] раз.

Структура данных для приоритетной очереди	Асимптотика времени работы
Наивная реализация	[math]O(V^2+E)[/math]
Двоичная куча	[math]O(E\log{V})[/math]
Фибоначчиева куча	[math]O(V\log{V}+E)[/math]

См. также

• Алгоритм Краскала
• Алгоритм Борувки

Источники информации

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — с.653 — 656.— ISBN 978-5-8459-0857-5 (рус.)
• Википедия - Алгоритм Прима
• Wikipedia - Prim's algorithm
• e-maxx - Минимальное остовное дерево. Алгоритм Прима