Рёберный граф
Версия от 00:41, 10 января 2015; SergeyBud (обсуждение | вклад)
| Определение: |
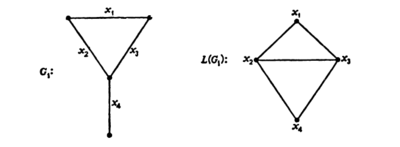
Пусть задан граф , тогда его рёберным графом называется граф, для которого верны следующие утверждения
|
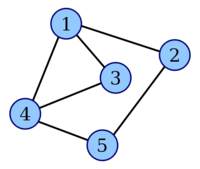
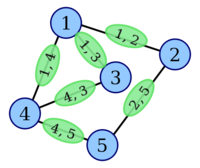
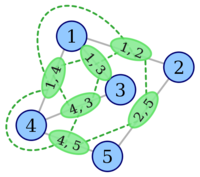
Построение
Свойства
| Утверждение: |
Рёберный граф связного графа связен. |
| Если связен, он содержит путь, соединяющий любые два его ребра, что переводится в путь графа , содержащий любые две вершины графа . |
| Утверждение: |
Задача о максимальном независимом множестве для рёберного графа соответствует задаче нахождения максимального паросочетания в исходном графе. |
| Утверждение: |
Рёберное хроматическое число графа равно вершинному хроматическому числу его рёберного графа . |
| Утверждение: |
Рёберный граф рёберно-транзитивного графа является вершинно-транзитивным графом. |
| Утверждение: |
Если граф — Эйлеров граф, то его рёберный граф является Гамильтоновым графом. |
| Утверждение: |
Ребра графа можно разбить на полные подграфы таким образом, чтобы ни одна из вершин не принадлежала более чем двум подграфам. |
| Утверждение: |
Реберный граф реберного графа не является исходным графом . |
| Контрпримером является граф и раздела Построение. Построив по указанному принципу реберный граф к графу , мы убедимся, что он не совпадает с исходным графом . |
| Теорема: |
Если — это -граф с вершинами, имеющими степени , то имеет вершин и ребер, где
|
| Доказательство: |
|
По определению реберного графа граф имеет вершин. Каждые ребер, инцидентных вершине , дают вклад в число ребер графа , так что |
Источники информации
- Wikipedia — Реберные графы
- Харари Фрэнк Теория графов: Пер. с англ./ Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 296 с. — ISBN 978-5-397-00622-4.(Глава 8: Реберные графы. стр. 91-104)