Алгоритм Укконена

Материал из Викиконспекты
Версия от 10:43, 14 апреля 2015; KK (обсуждение | вклад) (→‎Линейный алгоритм)
Перейти к: навигация, поиск

Алгоритм Укконена (англ. Ukkonen's algorithm) — алгоритм построения суффиксного дерева для заданной строки [math]s[/math] за линейное время.

Алгоритм за O(n3)

Рассмотрим сначала наивный метод, который строит дерево за время [math]O(n^3)[/math], где [math]n[/math] — длина исходной строки [math]s[/math]. В дальнейшем данный алгоритм будет оптимизирован таким образом, что будет достигнута линейная скорость работы.

Определение:
Неявное суффиксное дерево (англ. implicit suffix tree, IST) строки [math]S[/math] — это суффиксное дерево, построенное для строки [math]S[/math] без добавления [math]\$[/math].
Пример построения суффиксного дерева алгоритмом Укконена.

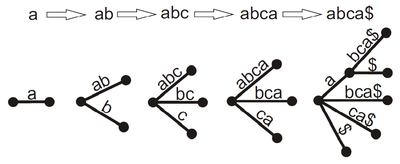
Алгоритм последовательно строит неявные суффиксные деревья для всех префиксов исходного текста [math]S = s_{1}s_{2}...s_{n}[/math]. На [math]i[/math]-ой итерации неявное суффиксное дерево [math]\tau_{i-1}[/math] для префикса [math]s[1..i-1][/math] достраивается до [math]\tau_{i}[/math] для префикса [math]s[1..i][/math]. Будем спускаться от корня дерева до конца каждого суффикса префикса [math]s[1..i-1][/math] и дописывать к ним символ [math]s_{i}[/math]. Не стоит забывать, что [math]s_{i}[/math] является суффиксом [math]s[1..i][/math] , поэтому его тоже нужно добавить в дерево.

Замечание: Казалось бы, что можно просто добавлять все суффиксы строки в дерево по очереди, и это уже было бы [math]O(n^2)[/math]. Но оптимизировать такой квадратичный алгоритм до линейного немного сложнее, хотя именно это и делает Алгоритм МакКрейта. Оптимизируя описанный выше алгоритм, мы получим более простой алгоритм за [math]O(n)[/math].

Алгоритм состоит из [math]n[/math] итераций так как в исходном тексте [math]O(n)[/math] суффиксов. На каждой фазе происходит продление всех суффиксов по порядку, что требует [math]O(n^2)[/math] времени. Следовательно, общая асимптотика алгоритма [math]O(n^3)[/math].

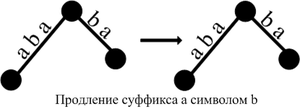
Продление суффиксов

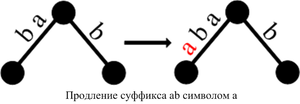
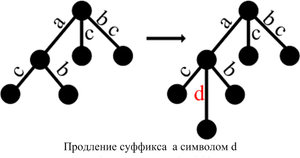
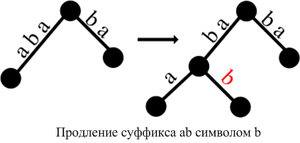
Ниже приведены возможные случаи, которые могут возникнуть при добавлении символа [math]s_{i}[/math] ко всем суффиксам префикса [math]s[1..i-1][/math].

Случай Правило Пример
1. Продление листа Пусть суффикс [math]s[k..i-1][/math] заканчивается в листе. Добавим [math]s_{i}[/math] в конец подстроки, которой помечено ребро, ведущее в этот лист. ExampleUkkonen3.png
2.1 Создание листа Пусть суффикс [math]s[k..i-1][/math] заканчивается в вершине, не являющейся листом, из которой нет пути по символу [math]s_{i}[/math]. Создадим новый лист, в который из текущей вершины ведет дуга с пометкой [math]s_{i}[/math]. ExampleUkkonen4.png
2.2 Ответвление Пусть суффикс [math]s[k..i-1][/math] заканчивается на ребре, [math]t[1..p-1][/math] совпадает с концом [math]s[k..i-1][/math] и [math]t_{p}\ne s_{i}[/math]. Разобьем текущее ребро новой вершиной на [math]t[1..p-1][/math] и [math]t[p..l][/math], где [math]l[/math] — длина метки ребра, и подвесим к ней еще одного ребенка с дугой, помеченной [math]s_{i}[/math]. ExampleUkkonen5.png
3 Ничего не делать Пусть суффикс [math]s[k..i-1][/math] заканчивается в вершине, из которой есть путь по [math]s_{i}[/math]. Тогда ничего делать не надо. ExampleUkkonen6.png

Суффиксные ссылки

Определение:
Пусть [math]x\alpha[/math] обозначает произвольную строку, где [math]x[/math] — ее первый символ, а [math]\alpha[/math] — оставшаяся подстрока (возможно пустая). Если для внутренней вершины [math]v[/math] с путевой меткой [math]x\alpha[/math] существует другая вершина [math]s(v)[/math] с путевой меткой [math]\alpha[/math], то ссылка из [math]v[/math] в [math]s(v)[/math] называется суффиксной ссылкой (англ. suffix link).


Лемма (Существование суффиксных ссылок):
Для любой внутренней вершины [math]v[/math] суффиксного дерева существует суффиксная ссылка, ведущая в некоторую внутреннюю вершину [math]u[/math].
Доказательство:
[math]\triangleright[/math]
Рассмотрим внутренную вершину [math]v[/math] с путевой меткой [math]t[i..j][/math]. Так как эта вершина внутренняя, ее путевая метка ветвится справа в исходной строке. Тогда очевидно подстрока [math]t[i+1..j][/math] тоже ветвится справа в исходной строке, и ей соответствует некоторая внутренняя вершина [math]u[/math]. По определению суффиксная ссылка вершины [math]v [/math] ведет в [math] u[/math]
[math]\triangleleft[/math]

Использование суффиксных ссылок

Иллюстрация использования суффиксных ссылок.

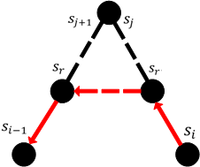
Суффиксные ссылки используются для того, чтобы можно было быстро перейти от конца одного суффикса к концу другого, а не спускаться каждый раз от корня. Пусть мы только что продлили суффикс [math]s[j..i-1][/math] до суффикса [math]s[j..i][/math] и стоим в вершине, в которую ведет ребро с пометкой [math]t[k+1..r][/math], содержащей конец текущего суффикса. Найдем с помощью построенных ссылок конец суффикса [math]s[j+1..i-1][/math]. Пройдем вверх по дереву до ближайшей внутренней вершины [math]v[/math], в которую ведет ребро с пометкой [math]t[p..k][/math]. У вершины [math]v[/math] есть суффиксная ссылка, так как ссылка для новой внутренней вершины строится внутри фазы ее создания. Пусть суффиксная ссылка ведет в вершину [math]u[/math], которой соответствует пометка [math]t[h..k][/math] ([math]h[/math] и [math]p[/math] могут быть не равны). Теперь пройдем от вершины [math]u[/math] вниз по дереву к концу суффикса [math]s[j+1..i-1][/math], и сделаем продление до суффикса [math]s[j+1..i][/math].

Построение суффиксных ссылок

Заметим что в процессе построения суффиксного дерева уже построенные суффиксные ссылки никак не изменяются. Опишем процесс построения суффиксной ссылки для новой созданной внутренней вершины. Пусть в результате очередного продления была создана новая внутренняя вершина [math]v[/math] с путевой меткой [math]t[l..r][/math]. Не будем специально искать, куда должна указывать ссылка. Перейдем к следующему шагу текущей фазы, на котором в дерево будет добавлен суффикс [math]s[j+1..i][/math]. Этот суффикс может так же оканчиваться на ребре, но тогда будет создана новая внутренняя вершина [math]u[/math], по определению суффиксная ссылка из вершины [math]v[/math] ведет в [math]u[/math].

Оценка числа переходов

Определение:
Глубиной вершины [math]d(v)[/math] назовем число ребер на пути от корня до вершины [math]v[/math]


Лемма:
При переходе по суффиксной ссылке глубина уменьшается не более чем на [math]1[/math].
Доказательство:
[math]\triangleright[/math]
Пусть мы переходим из вершины [math] v [/math] с путевой меткой [math]t[i..j][/math] по суффиксной ссылке в вершину [math] u [/math] с путевой меткой [math]t[i+1..j][/math] Определим множество [math] A [/math] как множество вершин на пути от корня до [math] u [/math], исключая корень. Множество [math] B [/math] определим как множество вершин на пути от корня до [math] v [/math], исключая корень. Если длина первого ребра на пути от корня до [math] v [/math] равна единице, то выкинем из множества [math]B[/math] вершину, в которую ведет это ребро. Итого по построению получаем: [math]|A| = d(u)[/math], [math]|B| \ge d(v) - 1[/math]. Теперь заметим, что суффиксная ссылка из любой вершины множества [math]B[/math] ведет в некоторую вершину множества [math] A[/math], и очевидно суффиксные ссылки из разных вершин ведут в разные вершины, поэтому [math]|A| \ge |B|[/math], а значит [math]d(u) \geqslant d(v) - 1[/math]
[math]\triangleleft[/math]
Лемма:
Число переходов по ребрам внутри фазы номер [math]i[/math] не превышает [math]4i[/math]
Доказательство:
[math]\triangleright[/math]
Оценим количество переходов по ребрам при поиске конца суффикса. Переход до ближайшей внутренней вершины уменьшает высоту на [math]1[/math]. Переход по суффиксной ссылке уменьшает высоту не более чем на [math]1[/math] (по лемме, доказанной выше). Значит в течение одной фазы вверх мы переходим не более [math]2i[/math] раз. Но внутри одной фазы начальная глубина не меньше конечной (так как длины суффиксов убывают до [math]1[/math]), поэтому вниз мы могли пройти не более [math]2i[/math] ребер. Итого получаем оценку [math]4i[/math].
[math]\triangleleft[/math]

Асимтотика алгоритма с использованием суффиксных ссылок

Благодаря суффиксным ссылкам количество действий на одной итерации снижается с [math]O(n^2)[/math] до [math]O(n)[/math], так как по доказанной выше лемме на каждом шаге мы делаем не более [math]O(n)[/math] переходов. Следовательно, общая асимптотика алгоритма улучшилась до [math]O(n^2)[/math].

Линейный алгоритм

Чтобы улучшить время работы данного алгоритма до [math]O(n)[/math], нужно использовать линейное количество памяти, поэтому метка каждого ребра будет храниться как два числа — позиции ее самого левого и самого правого символов в исходном тексте.

Лемма (Стал листом — листом и останешься):
Если в какой-то момент работы алгоритма Укконена будет создан лист с меткой [math]i[/math] (для суффикса, начинающегося в позиции [math]i[/math] строки [math]S[/math]), он останется листом во всех последовательных деревьях, созданных алгоритмом.
Доказательство:
[math]\triangleright[/math]
Это верно потому, что у алгоритма нет механизма продолжения листового ребра дальше текущего листа. Если есть лист с суффиксом [math]i[/math], правило продолжения 1 будет применяться для продолжения [math]i[/math] на всех последующих фазах.
[math]\triangleleft[/math]
Лемма (Правило 3 заканчивает дело):
В любой фазе, если правило продления 3 применяется в продолжении [math]i[/math], оно будет реализовываться во всех дальнейших продолжениях (от [math]i+1[/math] по [math]j+1[/math]) до конца фазы.
Доказательство:
[math]\triangleright[/math]
При использовании правила продолжения 3 путь, помеченный [math]s[i..j][/math] в текущем дереве, должен продолжаться символом [math]j+1[/math], и точно так же продолжается путь, помеченный [math]s[i+1..j][/math], поэтому правило 3 применяется в продолжениях [math]i+1, i+2, ..., j+1[/math]
[math]\triangleleft[/math]

Когда используется 3-е правило продления суффикса, никакой работы делать не нужно, так как требуемый суффикс уже в дереве есть. Поэтому можно заканчивать текущую итерацию после первого же использования этого правила. Так как лист навсегда останется листом, зададим метку ребра ведущего в этот лист как [math]t[i..n][/math], где [math]n[/math] — это длина исходного текста. На следующих итерациях к этому ребру может применяться правило ответвления, но при этом будет меняться только левый(начальный) индекс [math]i[/math]. Таким образом мы сможем удлинять все суффиксы, заканчивающиеся в листах за [math]O(1)[/math].

Итоговая оценка времени работы

Все неявные продления листов суммарно можно выполнить за [math]O(n)[/math] (по первой лемме). По второй лемме алгоритм делает не более [math]2n[/math] явных продлений. Таким образом, в течение всех [math]n[/math] итерация суммарно выполняется не более [math]O(n)[/math] продлений, следовательно, с использованием всех приведенных эвристик, алгоритм Укконена работает за [math]O(n)[/math].

Минусы алгоритма Укконена

Не смотря на то, что данный алгоритм является одним из самых простых в понимании алгоритмов для построения суффиксных деревьев и использует online подход, у него есть серьезные недостатки, из-за которых его нечасто используют на практике:

  1. Константное время на одну итерацию — это амортизированная оценка, в худшем случае одна фаза может выполняться за [math]O(n)[/math] времени. Например, алгоритм Дэни Бреслауера и Джузеппе Итальяно[1], хоть и строит дерево за [math]O(n \log \log n)[/math], но на одну итерацию в худшем случае тратит [math]O(\log \log n)[/math] времени.
  2. Существенно использует константность размера алфавита. Например, алгоритм Фарах-Колтона строит суффиксное дерево за линейное время независимо от размера алфавита.
  3. На сегодняшний день существуют кэш-эффективные алгоритмы, которые превосходят алгоритм Укконена на современных процессорах[2].

Реализация

 // s — исходный текст
 // n — длина текста
 // t — массив, в котором хранится дерево
 // sz — размер суффиксного дерева

 struct node 
   l, r, par,link
   next[]
   function len():
     return r - l
   function get(c):
     if !next.count(c)
       next[c] = -1
     return next[c]

 struct state
   v // номер вершины, в которой мы остановились на предыдущей итерации
   pos // позиция на метке ребра, ведущего в эту вершину
 
 state ptr(0, 0) // указатель на конец самого длинного не уникального суффикса

 function go(st, l, r):
   while l < r
     if st.pos == t[st.v].len()
       st = state(t[st.v].get(s[l]), 0)
       if st.v == -1
         return st
     else
       if s[t[st.v].l + st.pos] [math]\ne[/math] s[l]
         return state(-1, -1)
       if r - l < t[st.v].len() - st.pos
         return state(st.v, st.pos + r - l)
       l = l + t[st.v].len() - st.pos
       st.pos = t[st.v].len()
   return st

 function split(st):
   if st.pos == t[st.v].len()
     return st.v
   if st.pos == 0
     return t[st.v].par
   node v = t[st.v]
   id = sz
   sz = sz + 1
   t[id] = node(v.l, v.l + st.pos, v.par)
   t[v.par].get(s[v.l]) = id
   t[id].get(s[v.l + st.pos]) = st.v
   t[st.v].par = id
   t[st.v].l = t[st.v].l + st.pos
   return id
 
 function getLink(v):
   if t[v].link [math]\ne[/math] -1
     return t[v].link
   if t[v].par == -1
     return 0
   to = getLink(t[v].par)
   return t[v].link = split(go(state(to, t[to].len()), t[v].l + (t[v].par==0), t[v].r))

 funciton treeExtend(pos):
   while true
     state nptr = go(ptr, pos, pos + 1)
     if nptr.v [math]\ne[/math] -1
       ptr = nptr
       return
     mid = split(ptr)
     leaf = sz
     sz = sz + 1
     t[leaf] = node(pos, n, mid)
     t[mid].get(s[pos]) = leaf
     ptr.v = getLink(mid)
     ptr.pos = t[ptr.v].len()
     if !mid
       break

 function buildTree():
   sz = 1
   for i = 0...n
     treeExtend(i)

См. также

Примечания

Источники

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Алгоритм_Укконена&oldid=45503»