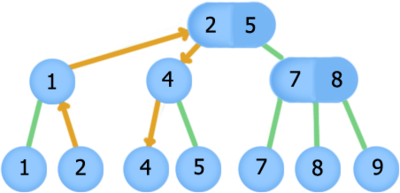
2-3 дерево
Свойства
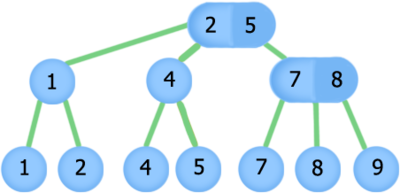
2-3 дерево — сбалансированное дерево поиска, обладающее следующими свойствами:
- нелистовые вершины имеют либо , либо сына,
- нелистовая вершина, имеющая двух сыновей, хранит максимум левого поддерева. Нелистовая вершина, имеющая трех сыновей, хранит два значения. Первое значение хранит максимум левого поддерева, второе максимум центрального поддерева,
- сыновья упорядочены по значению максимума поддерева сына,
- все листья лежат на одной глубине,
- Высота 2-3 дерева , где — количество элементов в дереве.
Операции
Введем следующие обозначения:
- — корень 2-3 дерева.
Каждый узел дерева обладает полями:
- — родитель узла,
- — сыновья узла,
- — ключи узла,
- — количество сыновей.
Поиск
- — искомое значение,
- — текущая вершина в дереве.
Изначально . Будем просматривать ключи в узлах, пока узел не является листом. Рассмотрим два случая:
- у текущей вершины два сына. Если её значение меньше , то , иначе .
- у текущей вершины три сына. Если второе значение меньше , то . Если первое значение меньше , то , иначе .
T search(T x):
Node t = root
while (t не является листом)
if (t.length == 2)
if (t.keys[0] < x)
t = t.sons[1]
else t = t.sons[0]
else if (t.keys[1] < x)
t = t.sons[2]
else if (t.keys[0] < x)
t = t.sons[1]
else t = t.sons[0]
return t.keys[0]
Вставка элемента
- — добавляемое значение,
- — текущая вершина в дереве. Изначально .
Если корня не существует — дерево пустое, то новый элемент и будет корнем (одновременно и листом). Иначе поступим следующим образом:
Найдем сперва, где бы находился элемент, применив . Далее проверим есть ли у этого узла родитель, если его нет, то в дереве всего один элемент — лист. Возьмем этот лист и новый узел, и создадим для них родителя, лист и новый узел расположим в порядке возрастания.
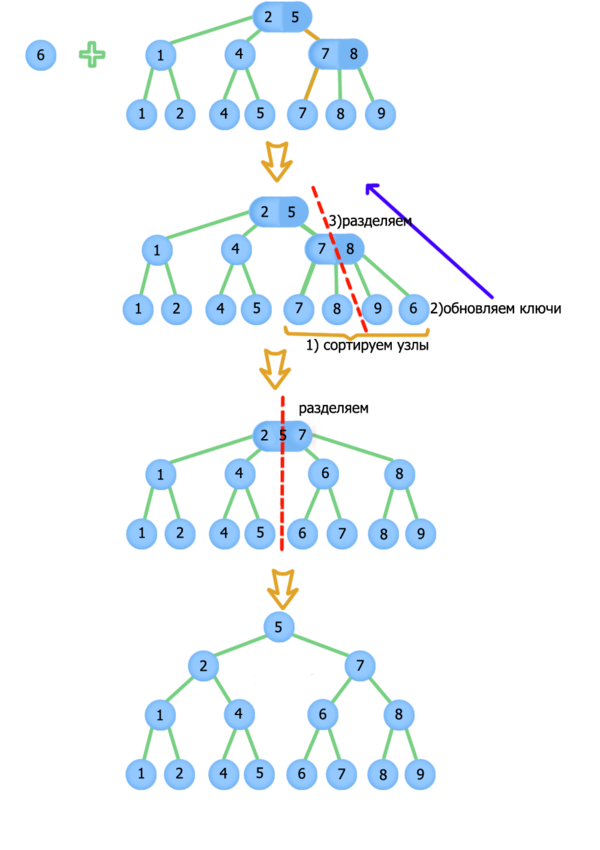
Если родитель существует, то подвесим к нему ещё одного сына. Если сыновей стало , то разделим родителя на два узла, и повторим разделение теперь для его родителя, ведь у него тоже могло быть уже сына, а мы разделили и у него стало на сына больше. (перед разделением обновим ключи).
function splitParent(Node t):
if (t.length > 3)
Node a = Node(sons = {t.sons[2], t.sons[3]}, keys = {t.keys[2]}, parent = t.parent, a.length = 2)
t.sons[2].parent = a
t.sons[3].parent = a
t.length = 2
t.sons[2] = null
t.sons[3] = null
if (t.parent != null)
t.parent[t.length] = a
t.length++
сортируем сыновей у t.parent
splitParent(t.parent)
else // мы расщепили корень, надо подвесить его к общему родителю, который будет новым корнем
Node t = root
root.sons[0] = t
root.sons[1] = a
t.parent = root
a.parent = root
root.length = 2
сортируем сыновей у root
Если сыновей стало , то ничего не делаем. Далее необходимо восстановить ключи на пути от новой вершины до корня:
function updateKeys(Node t):
Node a = t.parent
while (a != null)
for i = 0 .. a.length - 1
a.keys[i] = max(a.sons[i]) // max — возвращает максимальное значение в поддереве.
a = a.parent // Примечание: max легко находить, если хранить максимум
// правого поддерева в каждом узле — это значение и будет max(a.sons[i])
необходимо запускать от нового узла. Добавление элемента:
function insert(T x):
Node n = Node(x)
if (root == null)
root = n
return
Node a = search(x)
if (a.parent == null)
Node t = root
root.sons[0] = t
root.sons[1] = n
t.parent = root
n.parent = root
root.length = 2
сортируем сыновей у root
else
Node p = a.parent
p.sons[p.length] = n
p.length++
n.parent = p
сортируем сыновей у p
updateKeys(n)
split(n)
updateKeys(n)
Так как мы спускаемся один раз, и поднимаемся вверх при расщеплении родителей не более одного раза, то работает за .
Примеры добавления:
Удаление элемента
- — значение удаляемого узла,
- — текущий узел.
- — любой брат .
Пусть изначально — узел, где находится .
Если у не существует родителя, то это корень. Удалим его.
Если у существует родитель, и у него строго больше сыновей, то просто удалим , а у уменьшим количество детей.
Если у родителя сына, то найдем у любого соседнего листа его родителя, обозначим его за . Обозначим отца соседнего листа за .Рассмотрим возможные случаи:
- не существует, тогда мы удаляем одного из сыновей корня, тогда другой сын становится новым корнем,
- у оказалось сына, у оказалось 2 сына. Подвесим к и удалим , но у отца не изменим количество детей. Так у отца оказалось тоже два сына,повторяем для него такие же рассуждения.
- у оказалось сына, у оказалось 2 сына. Подвесим к и удалим , а у отца уменьшим количество детей. Так как у оказалось четыре сына, то необходимо его расщепить. Теперь у отца оказалось два сына и все узлы 2-3 дерева корректны.
- у оказалось сына, у оказалось 2 сына. Подвесим к и удалим , а у отца уменьшим количество детей. Так как у оказалось три сына, а у отца все ещё больше одного сына, то все узлы 2-3 дерева корректны.
- у оказалось сына, у оказалось 3 сына. Подвесим к и удалим , а у отца уменьшим количество детей. Так как у оказалось четыре сына, то расщепим его, теперь у отца вновь три сына и все узлы 2-3 дерева корректны.
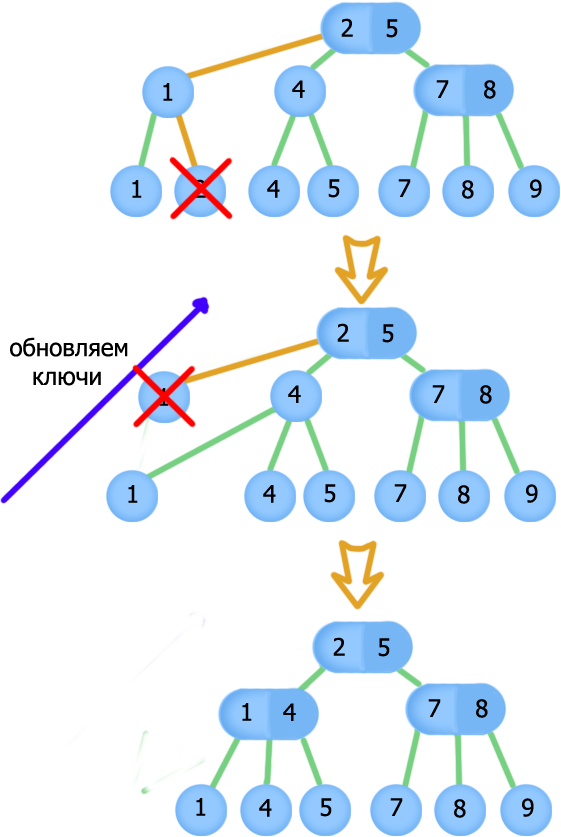
Обобщим алгоритм при удалении когда у родителя два сына(ниже мы никогда не уменьшаем количество детей у ):
- Если p не существует, то оказывается, что мы сейчас удаляем какого-то из сыновей корня (для определенности далее левого, с правым аналогично). Тогда теперь правый сын становится корнем. На этом удаление заканчивается.
- Если p существует, то удалим , а его брата () перецепим к . Теперь у могло оказаться сына, поэтому повторим аналогичные действия из : вызовем и . Теперь рекурсивно удалим .
В результате мы получаем корректное по структуре 2-3 дерево, но у нас есть нарушение в ключах в узлах, исправим их с помощью , запустившись от .
Следующий и предыдущий
- — поисковый параметр,
- — текущий узел.
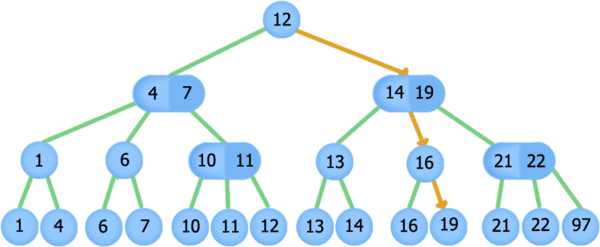
В силу того, что наши узлы отсортированы по максимуму в поддереве, то следующий объект это соседний лист справа. Попасть туда можно следующим образом: будем подниматься вверх, пока у нас не появится первой возможности свернуть направо вниз. Как только мы свернули направо вниз, будем идти всегда влево. Таким образом, мы окажемся в соседнем листе. Если мы не смогли ни разу свернуть направо вниз, и пришли в корень, то следующего объекта не существует. Случай с предыдущим симметричен.
T next(T x)
Node t = search(x)
if (t.keys[0] > x) //x не было в дереве, и мы нашли следующий сразу
return t
while (t != null)
t = t.parent
if (можно свернуть направо вниз)
в t помещаем вершину, в которую свернули
while (пока t — не лист)
t = t.sons[0]
return t
return t.keys[0];
Нахождение m следующих элементов
B+ деревья, поддерживают операцию , которая позволяет находить m следующих элементов. Наивная реализация выглядит следующим образом: будем вызывать раз поиск следующего элемента, такое решение работает за . Но 2-3 деревья, позволяют находить m следующих элементов за , что значительно ускоряет поиск при больших . По построению, все листья у нас отсортированы в порядке возрастания, воспользуемся этим для нахождения m элементов. Нам необходимо связать листья, для этого модифицируем и . Добавим к узлам следующие поля:
- — указывает на правый лист,
- — указывает на левый лист.
Пусть — добавленный узел. Изменим следующим образом: в самом конце, после того как мы уже обновили все ключи, найдем и запишем ссылку на него в . Аналогично с левым.
Пусть — удаляемый узел. Изменим следующим образом: в самом начале, до удаления , найдем следующий и запишем в правый лист относительно . С левым поступим аналогично.
В итоге, мы имеем двусвязный список в листьях, и чтобы нам вывести элементов, нам достаточно один раз найти нужный элемент и пробежаться вправо на элементов.
См. также
Источники информации
- is.ifmo.ru — Визуализатор 2-3 дерева
- rain.ifmo.ru — Визуализатор 2-3 дерева
- Википедия — 2-3 дерево
- Д. Кнут «Искусство программирования. Сортировка и поиск» — стр. 508 - 509