Турниры
| Определение: |
| Турнир (англ. Tournament) — ориентированный граф, между любой парой различных вершин которого есть ровно одно ориентированное ребро. |
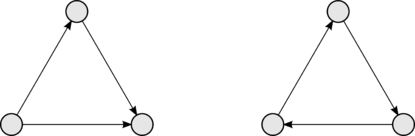
Имя турнир исходит из графической интерпретации исходов кругового турнира, в котором каждый игрок встречается в схватке с каждым другим игроком ровно раз, и в котором не может быть ничьих. В орграфе турнира вершины соответствуют игрокам. Дуга между каждой парой игроков ориентирована от выигравшего к проигравшему. Если игрок побеждает игрока , то говорят, что доминирует над .
Оценка количества турниров в графе
Если в турнире опустить ориентацию ребер, то мы получим полный граф. А так как существует два варианта ориентации каждого ребра, то количество турниров в графе из вершин равно .
Транзитивность
Турнир, в котором , называется транзитивным. В транзитивном турнире вершины могут быть полностью упорядочены в порядке достижимости.
Следующие утверждения для турнира с n вершинами эквивалентны:
- транзитивен.
- ацикличен.
- не содержит циклов длины 3.
- Последовательность числа выигрышей (множество полуисходов) есть .
- содержит ровно один гамильтонов путь.
Транзитивные турниры играют существенную роль в теории Рамсея, изучающей условия, при которых в произвольно формируемых математических объектах обязан появиться некоторый порядок. В частности, любой турнир с вершинами содержит транзитивный подтурнир с вершинами. Для его построения выберем любую вершину как часть этого подтурнира и построим подтурнир рекурсивно на множестве либо входящих соседей вершины , либо на множестве исходящих соседей, в зависимости от того, какое множество больше.
Парадоксальные турниры
Игрок, выигравший все игры, естественно, будет победителем турнира. Однако, как показывает существование нетранзитивных турниров, такого игрока может не оказаться. Турнир, в котором каждый игрок проигрывает хотя бы одну игру называется 1-парадоксальным турниром. Обобщая, Турнир называется -парадоксальным, если для любого -элементного подмножества множества существует вершина в , такая что для всех .
Конденсация
Конденсация любого турнира является транзитивным турниром. Таким образом, даже если турнир не является транзитивным, сильно связанные компоненты турнира могут быть полностью упорядочены.
Сильно связные турниры
| Определение: |
| Турнир называется сильно связным, если из любой вершины существуют пути до всех других. |
| Определение: |
| Турнир называется гамильтоновым, если он содержит гамильтонов цикл. |
Не все турниры гамильтоновы. Определение не исключает существование вершины с или равной нулю — в первую нельзя войти, а из второй — выйти. Однако отсутствие таких вершин не означает, что турнир гамильтонов (пример — на рисунке справа).
Теорема Редеи-Камиона устанавливает 2 следующих факта:
- Все турниры полугамильтоновы.
- Турнир гамильтонов тогда и только тогда, когда он сильно связен.
См. также
Источники информации
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — ISBN 5-93972-076-5