Обсуждение участницы:Анна

Алгоритм разделения АВЛ-дерева на два, где в первом дереве все ключи меньше заданного x, а во втором - больше

Пусть у нас есть дерево [math]T[/math]. Мы должны разбить его на два дерева [math]T_{1}[/math] и [math]T_{2}[/math] такие, что [math]T_{1} \leqslant x[/math] и [math]x \lt T_{2}[/math].

Предположим, что корень нашего дерева [math]\leqslant x[/math], в таком случае все левое поддерево вместе с корнем после разделения отойдет в дерево [math]T_{1}[/math]. Тогда рекурсивно спускаемся в правое поддерево и там проверяем это условие (так как часть правого поддерева тоже может содержать ключи [math]\leqslant x[/math]). Если же корень оказался [math]\gt x[/math], то мы спускаемся той же рекурсией, но только в левое поддерево и ищем там.

Пусть мы пришли в поддерево [math]S[/math], корень которого [math]\leqslant x[/math]. В таком случае этот корень со своим левым поддеревом должен отойти в дерево [math]T_{1}[/math]. Поэтому мы делаем следующее: запоминаем ссылку на правое поддерево [math]S[/math], удаляем корень, запоминая его значение (не меняя конфигурацию дерева, то есть просто делаем ссылки на него NULL'ами). Таким образом, мы отделяем сбалансированное АВЛ-дерево (бывшее левое поддерево [math]S[/math]). Делаем новую вершину со значением бывшего корня правым листом самой правой вершины [math]S[/math] и запускаем балансировку. Обозначим полученное дерево за [math]T'[/math]. Теперь нам нужно объединить его с уже построенным ранее [math]T_{1}[/math] (оно может быть пустым, если мы первый раз нашли такое дерево [math]S[/math]). Для этого мы ищем в дереве [math]T_{1}[/math] самое правое поддерево [math]P[/math] высоты, равной высоте [math]T'[/math] (спускаясь от корня всегда в правые поддеревья). Делаем новое дерево [math]K[/math], сливая [math]P[/math] и [math]T'[/math] (очевидно, все ключи в [math]T_{1}[/math] меньше ключей в [math]T'[/math], поэтому мы можем это сделать). Теперь в дереве [math]T_{1}[/math] у отца вершины, в которой мы остановились при поиске дерева [math]P[/math], правым поддеревом делаем дерево [math]K[/math] и запускаем балансировку. После нужно спуститься в правое поддерево бывшего дерева [math]S[/math] (по ссылке, которую мы ранее запомнили) и обработать его.

Если мы пришли в поддерево [math]Q[/math], корень которого [math]\gt x[/math], совершаем аналогичные действия: делаем NULL'ами ссылки на корень [math]Q[/math], запоминая ссылку на его левое поддерево. Делаем новую вершину со значением бывшего корня левым листом самой левой вершины [math]Q[/math] и запускаем балансировку. Объединяем полученное АВЛ-дерево с уже построенным ранее [math]T_{2}[/math] аналогичным первому случаю способом, только теперь мы ищем самое левое поддерево [math]T_{2}[/math].

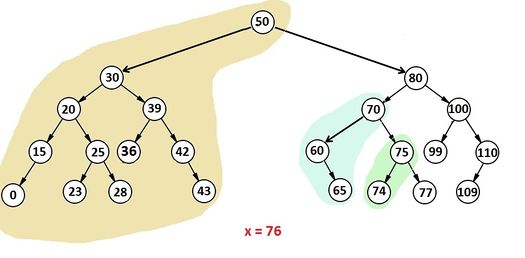
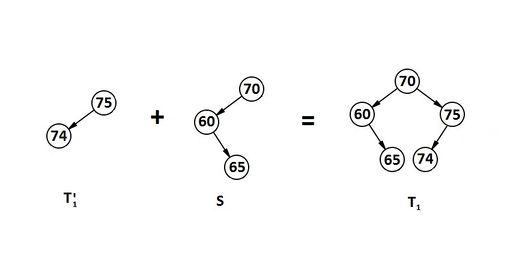
Рассмотри пример (рис. 1). Цветом выделены поддеревья, которые после разделения должны отойти в дерево [math]T_{1}[/math]. [math]x = 76[/math].

Рис. 1. Разделение АВЛ-дерева на два.

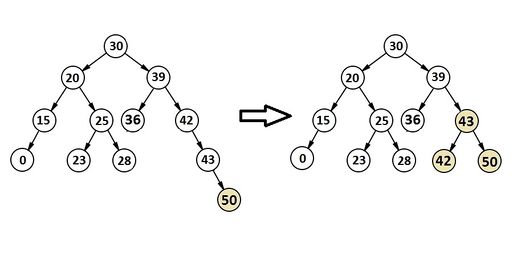
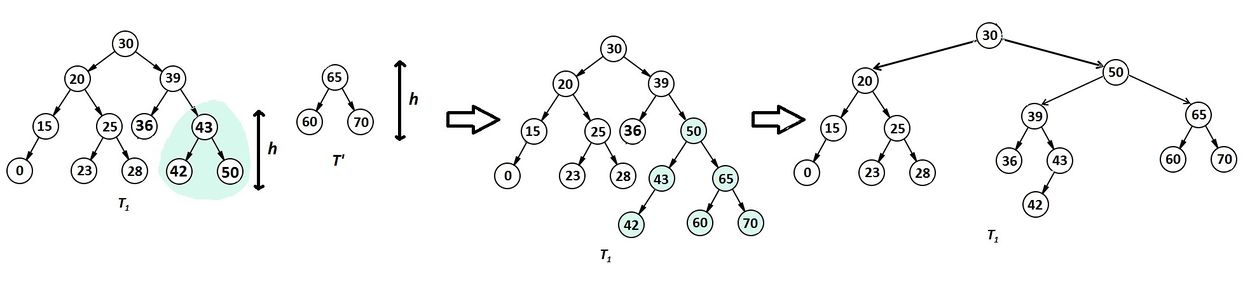
Корень дерева [math]\leqslant x[/math], поэтому он со всем выделенным поддеревом должен отойти в дерево [math]T_{1}[/math]. По описанному выше алгоритму отделяем это поддерево с корнем и делаем из них сбалансированное АВЛ-дерево [math]T'[/math] (рис. 2). Так как это первая ситуация, в которой корень рассматриваемого поддерева был [math]\leqslant x[/math], [math]T'[/math] становится [math]T_{1}[/math]. Далее по сохраненной ссылке спускаемся в правое поддерево. Его корень [math]\gt x[/math]. Следовательно, строим из него и его правого поддерева [math]T_{2}[/math] и спускаемся в левое поддерево. Снова корень [math]\leqslant x[/math]. Строим новое [math]T'[/math] и объединяем его с уже существующим [math]T_{1}[/math] (рис. 3).

Рис. 2. Создание T'.

Рис. 3. Объединение T' и T1.

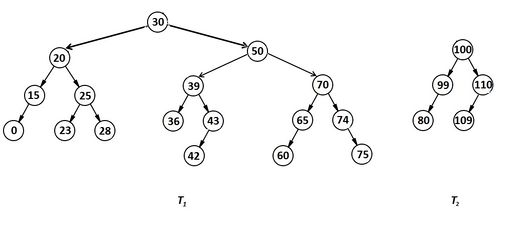
Далее действуем по алгоритму и в итоге получаем (рис. 4):

Рис. 4. АВЛ-деревья после разделения.

Данный алгоритм имеет сложность [math]O(\log^{2} n)[/math]. Рассмотрим решение, которое имеет сложность [math]O(\log{n})[/math].

Вернемся к примеру (рис. 1). Теперь рекурсивно спустимся вниз и оттуда будем строить деревья [math]T_{1}[/math] и [math]T_{2}[/math], передавая наверх корректные АВЛ-деревья. То есть для рис. 1 первым в дерево [math]T_{1}[/math] придет вершина [math]75[/math] с левым поддеревом (выделено светло-зеленым цветом), так как это корректное АВЛ-дерево, оно же и вернется из рекурсии. Далее мы попадем в вершину со значением [math]70[/math] и должны слить ее и ее левое поддерево (выделено светло-синим) с тем, что нам пришло. И сделать это нужно так, чтобы передать наверх корректное АВЛ-дерево. Будем действовать по такому алгоритму, пока не дойдем до вершины.

Пусть мы пришли в поддерево [math]S[/math] с корнем [math]\leqslant x[/math]. Тогда сольем его с уже построенным на тот момент [math]T_{1}[/math] ([math]T_{1}[/math] пришло снизу, а значит по условию рекурсии это корректное АВЛ-дерево, [math]S \leqslant T_{1}[/math] и [math]h(T_{1}) \leqslant h(S)[/math]). Но так как обычная процедура слияния сливает два АВЛ-дерева, а [math]S[/math] не является корректным АВЛ-деревом, мы немного ее изменим. Пусть мы в дереве [math]S[/math] нашли самое правое поддерево [math]K[/math], высота которого равна высоте [math]T_{1}[/math]. Тогда сделаем новое дерево [math]T'[/math], корнем которого будет вершина [math]S[/math] (без нее это дерево является сбалансированным), правым поддеревом — [math]T_{1}[/math], левым — [math]K[/math]. И подвесим [math]T'[/math] на то место, где мы остановились при поиске [math]K[/math]. Запустим балансировку. В случае, когда корень поддерева, в которое мы пришли, [math]\gt x[/math], все аналогично.

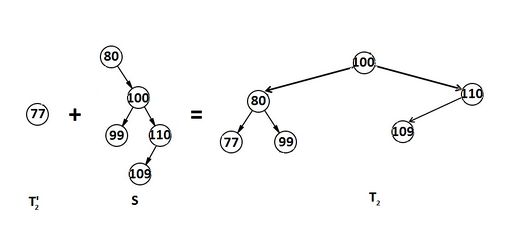
Разберем пример на рис. 1. Пусть мы рекурсивно спустились до узла [math]77[/math]. Ключ больше [math]x[/math], поэтому эта вершина станет деревом [math]T_{2}[/math] и передастся наверх. Теперь мы поднялись в узел [math]75[/math]. Он со своим левым поддеревом станет деревом [math]T_{1}[/math] и мы снова поднимемся наверх в узел [math]70[/math]. Он со своим левым поддеревом снова должен отойти в дерево [math]T_{1}[/math], и так как теперь дерево [math]T_{1}[/math] уже не пустое, то их надо слить. После слияния по описанному выше алгоритму получим (рис. 5)

Рис. 5.

После мы поднимемся в вершину с ключом [math]80[/math]. Она с правым поддеревом отойдет в дерево [math]T_{2}[/math] (рис. 6).

Рис. 6.

И на последней итерации мы поднимемся в корень дерева с ключом [math]50[/math], он с левым поддеревом отойдет в дерево [math]T_{1}[/math], после чего алгоритм завершится.

Пусть поддеревьев с ключами [math]\leqslant x[/math] оказалось больше, чем поддеревьев с ключами [math]\gt x[/math]. Докажем для них логарифмическую асимптотику. Дерево на последнем уровне имеет высоту [math]H_{k}[/math] (она может быть не равна [math]1[/math], если мы придём в [math]x[/math]). Его мы передаем наверх и вставляем в поддерево высотой [math]H_{k-1}[/math]. [math]H_{k} \leqslant H_{k-1}[/math], так как разница высот поддеревьев у любой вершины не больше [math]1[/math], и мы при переходе от [math]H_{k}[/math] к [math]H_{k-1}[/math] поднимаемся как минимум на одну вершину вверх. Слияние этих поддеревьев мы выполним за [math]H_{k-1} - H_{k}[/math], получим в итоге дерево высоты не большей, чем [math]H_{k-1}[/math]. Его мы передадим наверх, поэтому в следующий раз слияние будет выполнено за [math]H_{k-2} - H_{k - 1}[/math] и так далее. Таким образом мы получим [math](H - H_{1}) + (H_{1} - H_{2}) + (H_{2} - H_{3}) + \cdots + (H_{k - 1} - H_{k}) = H - H_{k} = O(\log{n})[/math].

Итоговая асимптотика алгоритма — [math]O(\log{n})[/math].

Гамма-алгоритм

Задача:

Определить, является ли граф планарным, и, если да, произвести его плоскую укладку.

Существует теорема Понтрягина-Куратовского, которая говорит, что граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных [math] K_{5} [/math] или [math] K_{3, 3} [/math]. Но этот критерий очень трудно проверить на практике, поэтому данная теорема представляет лишь теоретический интерес.

Чтобы проверить планарность графа и произвести его плоскую укладку, удобно пользоваться гамма-алгоритмом.

Входные данные

На вход алгоритму подаются графы со следующими свойствами:

1. Граф связный,
2. Граф содержит хотя бы один цикл,
3. Граф не имеет мостов.

Если нарушено свойство [math]1[/math], то граф нужно укладывать отдельно по компонентам связности. Если нарушено свойство [math]2[/math], то граф — дерево и нарисовать его плоскую укладку тривиально.

Более подробно рассмотрим случай, когда в графе [math]G[/math] нарушено свойство [math]3[/math]. Сначала все мосты нужно убрать, далее произвести отдельную укладку всех компонент следующим образом: уложим одну компоненту связности, а следующую компоненту, связанную с первой в графе [math]G[/math] мостом, будем рисовать в той грани, в которой лежит вершина, принадлежащая мосту. Иначе может сложиться ситуация, когда концевая вершина моста будет находиться внутри плоского графа, а следующая компонента - снаружи. Таким образом мы сможем соединить мостом нужные вершины. Далее будем так поступать с каждой новой компонентой.

Алгоритм

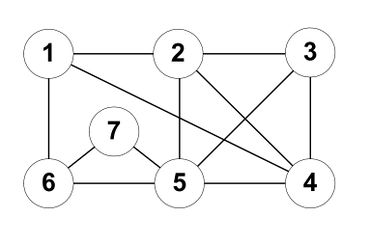
Рассмотрим работу алгоритма, параллельно разбирая на примере каждый шаг. Пусть дан граф [math]G[/math] (рис. 1).

Рис. 1. Исходный граф.

[math]1.[/math] Первый этап - инициализация алгоритма.

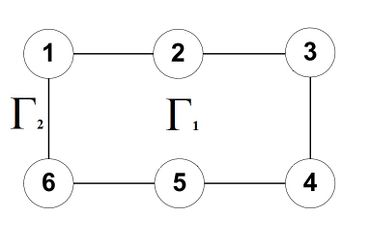
В графе [math]G[/math] выбирается любой простой цикл и производится его укладка на плоскость. Пусть в примере это будет цикл [math]\{1, 2, 3, 4, 5, 6\}[/math]. После его укладки получаем две грани: [math]\Gamma_{1}[/math] и [math]\Gamma_{2}[/math] (рис. 2).

Рис. 2. Укладка цикла на плоскость.

Уже уложенную во время работы алгоритма часть будем обозначать [math]G_{plane}[/math]. В примере сейчас [math]G_{plane}[/math] — выбранный цикл [math]\{1, 2, 3, 4, 5, 6\}[/math].

[math]2.[/math] Второй этап - общий шаг.

Построим множество сегментов. Каждый сегмент [math]S[/math] относительно уже построенного [math]G_{plane}[/math] представляет собой одно из двух:

1. ребро, оба конца которого принадлежат [math]G_{plane}[/math], но само оно не принадлежит [math]G_{plane}[/math],
2. связную компоненту графа [math]G \backslash G_{plane}[/math], дополненную всеми ребрами графа [math]G[/math] такими, у которых один из концов принадлежит связной компоненте, а второй принадлежит графу [math]G_{plane}[/math].

Вершины, одновременно принадлежащие [math]G_{plane}[/math] и какому-либо сегменту, назовем контактными. На рис. 3 изображены сегменты для нашего примера. Контактные вершины обведены в квадрат.

Рис. 3. Выделение сегментов.

Пусть в каком-то сегменте нет ни одной контактной вершины. В таком случае граф до выделения [math]G_{plane}[/math] был несвязным, что противоречит условию. Пусть контактная вершина в сегменте только одна. Это значит, что в графе был мост, чего быть не может так же по условию. Таким образом, в каждом сегменте имеется не менее двух контактных вершин. Соответственно, в каждом сегменте есть цепь между любой парой контактных вершин.