Бор

Бор (англ. trie, луч, нагруженное дерево) — структура данных для хранения набора строк, представляющая из себя подвешенное дерево с символами на рёбрах. Строки получаются прохождением из корня по рёбрам, записывая соответствующие им символы, до терминальной вершины. Размер бора линейно зависит от суммы длин всех строк, а поиск в бору занимает время, пропорциональное длине образца.

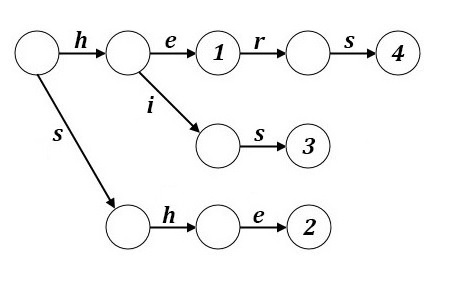
Пример

Бор для набора образцов [math] \{ \textbf{he}, \textbf{she}, \textbf{his}, \textbf{hers}\} [/math]:

Построение

Пусть [math]P = \{P_1,...,P_k\} [/math] — набор строк, называемый словарем.

Пусть [math]n = \sum_{i=1}^{k|P_i|}\limits |P_i|[/math].

Непосредственно построение:

1. Начинаем с дерева из одной вершины (корня).
2. Добавляем шаблоны [math]P_i[/math] один за другим.
3. Следуем из корня по рёбрам, отмеченным буквами из [math]P_i[/math], пока возможно.
4. Если [math]P_i[/math] заканчивается в [math]v[/math], сохраняем идентификатор [math]P_i[/math] (например, [math]i[/math]) в [math]v[/math] и отмечаем вершину [math]v[/math] как терминальную.
5. Если ребра, отмеченного очередной буквой [math]P_i[/math] нет, то создаем новые ребра и вершины для всех оставшихся символов [math]P_i[/math].

Это занимает, очевидно, [math]O(|P_1| + \ldots + |P_k|) = O(n)[/math] времени, так как поиск буквы, по которой нужно переходить, происходит за [math]O(1)[/math](в вершине есть указатели на буквы).

Поскольку на каждую вершину приходится [math]O(k)[/math] памяти, то использование памяти есть [math]O(nk)[/math].

Бор позволяет решать задачу поиска подстроки в строке, если построить его на множестве суффиксов исходной строки.

Существует еще одна модификация бора, называющаяся сжатый бор, отличающаяся от бора следующим улучшением: если у некоторой вершины исходящая степень равна 1, то эту вершину, ребро, входящее в нее, и ребро, исходящее из нее, можно объединить в одно ребро с более чем одним символом.

Поиск строки в бору

Задача:

Требуется найти слово в словаре.

Начинаем в корне, идем по рёбрам, отмеченным символами [math]S[/math], пока возможно. Если с последним символом [math]S[/math] мы приходим в вершину с сохраненным идентификатором, то [math]S[/math] — слово из словаря. Если в какой-то момент ребра, отмеченного нужным символом, не находится, то строки [math]S[/math] в словаре нет. Ясно, что это занимает [math]O (|S|)[/math] времени. Таким образом, бор — это эффективный способ хранить словарь и искать в нем слова.

Использование бора в качестве ассоциативного массива

Мы можем ввести для каждой вершины поле [math]\mathtt{value} \[/math]. Например, мы имеем [math]\mathtt{map}[/math][math]\lt [/math][math]\mathtt{string}\ , \mathtt{type}\ [/math][math]\gt [/math]. Будем искать ключ, спускаясь по бору. Соответственно, если на какой-то вершине нет пометки, что вершина является концом слова, то объекта в [math]\mathtt{map}[/math] нет. Если хотим добавить его, то ставим в вершину флаг конца слова и заносим значение. Работать такой алгоритм будет за [math]O(k)[/math], где [math]k[/math] — максимальная длина слова.

См. также

• Суффиксный массив
• Суффиксный бор
• Сжатое суффиксное дерево
• Алгоритм Ахо-Корасик

Источники информации

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — ISBN 5-8489-0857-4
• Бор. Построение бора