Толстая куча на избыточном счётчике

Толстое дерево

Определение:

Определяем толстое дерево (англ. Thick tree)

$F_k$ ранга

$k ~(k = 0, 1, 2 ~\dots )$ следующим образом:

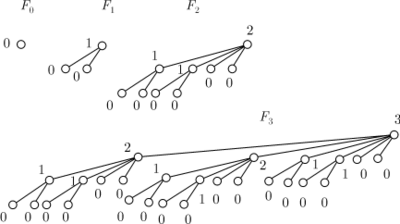
Толстое дерево $F_0$ ранга ноль состоит из единственного узла.
Толстое дерево $F_k$ ранга $k$ , для $k = 1, 2, 3,\dots$ , состоит из трех деревьев $F_{k-1}$ ранга $k$ ,таких, что корни двух из них являются самыми левыми потомками корня третьего.

Ранг узла

$x$ в толстом дереве определяется как ранг толстого поддерева с корнем в узле

$x$ .

Пример толстых деревьев

$F_0, F_1, F_2, F_3$

Утверждение:

Свойства толстых деревьев:

В толстом дереве ранга $k$ ровно $3^k$ узлов.
Для любого натурального числа $n$ существует лес из толстых деревьев, в котором ровно $n$ узлов. Такой лес можно построить, включив в него столько деревьев ранга $i$ , каково значение $i$ -го разряда представления числа $n$ в троичной системе счисления. Заметим, что для построения такого леса можно использовать и избыточные троичные представления.
Толстый лес из $n$ узлов содержит $O(n\log{n})$ деревьев.

Определение:

Лес будем называть нагруженным, если он состоит из нескольких толстых деревьев, ранги которых не обязательно попарно различны и узлам которых взаимно однозначно поставлены в соответствие элементы взвешенного множества.

Определение:

Узел (англ. Node) в нагруженном лесе назовем неправильным, если его ключ меньше ключа его родителя.

Определение:

Нагруженный лес назовем почти кучеобразным, если для каждого значения

$k$ в нем имеется не более двух неправильных узлов ранга

$k$ .

Толстые кучи

Здесь и далее "Толстая куча на избыточном счетчике" будет заменено на более лаконичное "Толстая куча".

Определение:

Толстая куча (англ. Thick heap, Fat heap) — это почти кучеобразный нагруженный лес.

Структура узла

Каждый узел толстой кучи будем представлять записью со следующими полями:

struct Node
  int key      // ключ элемента, приписанного узлу дерева
  Node parent   // указатель на родителя узла
  Node left    // указатель на ближайшего левого брата узла
  Node right    // указатель на ближайшего правого брата узла
  Node lChild    // указатель на самого левого сына
  int rank     // ранг узла

"Братья" (узлы корневых деревьев, а также сыновья каждого узла) объединены в двусвязный список при помощи указателей $left$ и $right$ . У самого левого (правого) "брата" в этом списке указатель $left$ ( $right$ ) равен $NULL$ .

Структура кучи

Толстую кучу будем представлять записью следующего вида:

struct FatHeap
  int rootCount []      // массив, соответствующий корневому счетчику
  int countViolation []   // массив, соответствующий счетчику нарушений
  Node minPointer    // указатель на элемент кучи с минимальным ключом
  int maxRank     // наибольший ранг среди рангов деревьев, присутствующих в куче

Представление леса списком

Избыточное представление чисел

Определение:

Избыточным

$b$ -арным представлением числа

$x$ будем называть последовательность

$d = d_n, d_{n-1}, ... d_0$ , такую что

$x = {\sum\limits^{n}_{i = 0} {d_i}}{b^i}$

где

$d_i \in \{0, 1, ..., b\}$ ,

$i \in \{0, 1, ..., n\}$

Определение:

Назовем

$b$ -арное избыточное представление числа регулярным, если в нем между любыми двумя цифрами, равными

$b$ , найдется цифра, отличная от

$b-1$ .

Определение:

Пусть

$L(i)$ — номер разряда, отличного от

$b-1$ и ближайшего слева от

$i$ -го разряда в регулярном

$b$ -арном избыточном представлении

$d = d_n, ... d_0$ .

Определим $L'(i)$ следующим образом:

$L'(i) = L(i)$ , если $d_i \in \{b-1, b-2\}$ и $d(L(i))=b$ ;
$L'(i)$ — произвольное число $\gt i$ , если $d_i \in \{b-1, b-2\}$ и $d(L(i))\lt b-1$ ;
$L'(i)$ — не определено, если $d \notin \{b-1, b-2 \}$ .

Величину

$L'(i)$ будем называть прямым указателем.

Фиксация цифры

Фиксацией цифры $b$ , стоящей в $i$ -м разряде представления $d$ , назовем операцию $\mathrm{fix(i)}$ , заключающуюся в обнулении цифры $d_i$ и инкрементировании цифры $d_{i+1}$ , при этом если $i=n$ , то полагаем $d_{i+1} = 1$ . При каждом выполнении операции фиксации будем обновлять значение $L'(i)$ . Очевидно, при $b\gt 2$ операцию $\mathrm{fix(i)}$ можно выполнить следующим образом:

fix(int i):
  if d[i] == b
    d[i] = 0
    d[i + 1]++
  if d[i + 1] == b - 1:
    L'[i] = L'[i + 1]
  else
    L'[i] = i + 1

Инкремент

Операцию $\mathrm{inc(i)}$ инкрементирования $i$ -й цифры избыточного представления $d$ можно выполнить так:

inc(int i):
  fix(i)
  if (d[i] == b - 1) or (d[i] == b - 2)
    fix(L'[i])
  d[i]++
  fix(i)

Декремент

Эта схема может быть расширена для выполнения за константное время декрементирования произвольной цифры добавлением дополнительного цифрового значения $b+1$ .

Представление приоритетной очереди основано на использовании так называемых избыточных счетчиков, позволяющих за время $O(1)$ инкрементировать любой разряд. Заметим, что использованные здесь счетчики — лишь один из способов реализации толстых куч. На самом деле, для их реализации подойдет произвольный d-арный счетчик, при условии, что трудоемкость инкрементирования любого его разряда является константной.

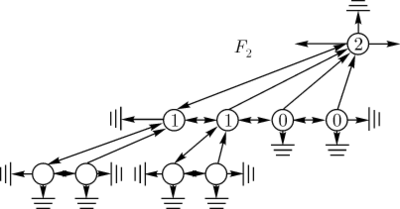
Корневой счетчик

Корневой счетчик состоит из избыточного троичного представления числа элементов в куче и набора списочных элементов.

Значение его $i$ -го разряда равно количеству деревьев ранга $i$ , присутствующих в куче. При таком определении избыточного корневого представления число, которое оно представляет, равно числу узлов в куче, так как толстое дерево ранга $i$ содержит ровно $3^i$ узлов. Заметим, что состояние избыточного корневого представления определяется неоднозначно. Очевидно, что для любой толстой кучи, состоящей из $n$ элементов, существует регулярное избыточное представление корневого счетчика. Списочный элемент, приписанный $i$ -му разряду избыточного корневого представления, — это указатель на список деревьев ранга $i$ , присутствующих в куче, образованный посредством указателей $right$ корневых узлов связываемых деревьев.

Утверждение (о корневом счетчике):

Из определения корневого счетчика следует:

Корневой счетчик позволяет иметь доступ к корню любого дерева ранга $i$ за время $O(1)$ .
Вставка толстого дерева ранга $i$ соответствует операции инкрементирования $i$ -го разряда корневого счетчика.
Удаление толстого поддерева ранга $i$ соответствует операции декрементирования $i$ -го разряда корневого счетчика.
Операции инкрементирования и декрементирования $i$ -го разряда корневого счетчика осуществляются за время $O(1)$ .

Корневой счетчик представляем расширяющимся массивом $rootCount$ , каждый элемент которого — запись с тремя полями:

$rootCount[i].Value$ — $i$ -й разряд равный количеству деревьев ранга $i$ .
$rootCount[i].forwardPointer$ — прямой указатель $i$ -го разряда.
$rootCount[i].listPointer$ — указатель на список деревьев ранга $i$ , присутствующих в толстой куче. Деревья в этом списке связаны при помощи указателя $Right$ корневых узлов связываемых деревьев. Если в куче нет деревьев ранга $i$ , то указатель $listPointer$ равен $NULL$ .

Заметим, что если значение равно нулю, то нам неважно значение указателя $rootCount[i].listPointer$ .

Инициализация

Чтобы время инициализации счетчиков было $O(1)$ , используем поразрядную их инициализацию. То есть будем добавлять новые разряды только тогда, когда возникает такая необходимость, и при этом инициализировать новый разряд сразу в обоих счетчиках. Для этого мы вводим переменную $maxRank$ , которая показывает нам, какая часть массивов счетчиков используется в данный момент.

При начальной инициализации необходимо установить счетчики в состояние, которое отвечает пустой куче. Очевидно, что в пустой куче не может быть никаких нарушений.

Обновление прямого указателя

Обновление прямого указателя $i$ -го разряда корневого счетчика заключается в выполнении следующего псевдокода:

updateForwardPionter(int i):
  if rootCount[i + 1].Value == 3 - 1
    rootCount[i].forwardPointer = rootCount[i + 1].forwardPointer
  else
    rootCount[i].forwardPointer = i + 1

Корректировка при вставке

Корректировка списочной части $i$ -го разряда корневого счетчика при вставке в кучу нового дерева ранга $i~(\mathrm{insertTree(i,p)})$ . Эта процедура вставляет новое дерево ранга $i$ (на него указывает указатель $p$ ) в списочную часть $i$ -го разряда корневого счетчика $rootCount$ выглядит так:

insertTree(i, p):
  p1 = rootCount[i].listPointer
  if rootCount[i].Value  $\ne$  0
    p.right = p1
  else
    p.right = NULL
  p.left = NULL
  rootCount[i].listPointer = p

Корректировка при удалении

Корректировка списочной части $i$ -го разряда корневого счетчика при удалении из кучи дерева ранга $i~(\mathrm{deleteTree(i,p)})$ . Эта процедура удаляет дерево ранга $i$ (на него указывает указатель $p$ ) из списочной части $i$ -го разряда корневого счетчика $rootCount$ . Будем считать, что указанное дерево присутствует в куче. Процедура заключается в выполнении следующего псевдокода:

deleteTree(i, p):
  p1 = rootCount[i].listPointer
  if p1 == p
    rootCount[i].listPointer = p.right
  j = 1
  while (j  $\le$  rootCount[i].Value) and (p1.right  $\ne$  p):
    j++
    p1 = p1.right
  p1.right = p.right

Связывание трех деревьев в одно

Связывание $\mathrm{fastening (p1, p2, p3)}$ трех толстых деревьев ранга $i$ в одно толстое дерево ранга $i+1$ . Эта функция принимает три указателя $p1, p2 ,p3$ на три разных толстых дерева одного и того же ранга $i$ и возвращает указатель на вновь сформированное дерево ранга $i+1$ . Процедура заключается в выполнении следующего псевдокода:

fastening (p1, p2, p3):
  if (p1.key  $\le$  p2.key) and (p1.Key  $\le$  p3.key)
    minP = p1
    p1 = p2
    p2 = p3
  if (p2.key  $\le$  p1.key) and (p2.key  $\le$  p3.key)
    minP = p2
    p1 = p1
    p2 = p3
  if (p3.key  $\le$  p1.key) and (p3.key  $\le$  p2.key)
    minP = p3
    p1 = p1
    p2 = p2
  p1.right = p2
  p1.left = NULL
  p1.parent = minP
  p2.right = minP.lChild
  p2.left = p1
  p2.parent = minP
  if minP.lChild  $\ne$  NULL
    minP.lChild.left = p2
  minP.lChild = p1
  minP.rank = minP.rank + 1
  minP.right = NULL
  minP.left = NULL
  return minP

Значение ключа элемента по указателю

Функция $\mathrm{getKey(p)}$ по указателю p на элемент определяет значение его ключа:

//под  $\infty$  нужно понимать нейтральный относительно минимума элемент.
getKey(p):
  if p == NULL
    min =  $\infty$ 
  else
    min = p.key
  return min

Узел с минимальным ключом

Функция $\mathrm{minKeyNodeRoot(p)}$ , которая по указателю $p$ на списочную часть разряда корневого счетчика возвращает указатель на корневой узел с минимальным ключом:

minKeyNodeRoot(p):
  p1 = p
  minP = p1
  while p1  $\ne$  NULL
    if p1.key < minP.key
      minP = p1
      p1 = p1.right
  return minP

Операция фиксации

Операция фиксации $\mathrm{rmFixRootCount(i)}$ для $i$ -го разряда корневого счетчика подразумевает, что его значение равно трем, а списочная часть содержит указатель на список деревьев ранга $i$ , состоящий ровно из трех деревьев. При выполнении этой операции значение в $i$ -м разряде — должно стать равным нулю, а значение в $i$ -м разряде увеличиться на единицу. То есть в куче не должно остаться деревьев ранга $i$ , а количество деревьев ранга $i+1$ должно увеличиться на единицу. Для этого следует удалить из кучи три присутствующих в ней дерева ранга $i$ , связать их в дерево ранга $i+1$ и вставить вновь полученное дерево в кучу. Следует учесть, что ранг нового дерева может стать больше, чем $maxRank$ , что потребует инициализации нового разряда. Для этого необходимо увеличить значение $maxRank$ на единицу и заполнить новое поле, а также провести инициализацию нового разряда.

rmFixRootCount(i)
  if maxRank == i
    maxRank = i + 1
    rootCount[i + 1].Value = 0
    countViolation[i + 1].Value = 0
  else
    updateForwardPointer(i + 1)
  rootCount[i].Value = 0
  p1 = rootCount[i].listPointer
  p2 = p1.right
  p3 = p2.right
  p = fastening(p1, p2, p3)
  rootCount[i].listPointer = NULL
  insertTree(i + 1, p)
  rootCount[i + 1].Value = rootCount[i + 1].Value + 1

Инкрементирование i-го разряда корневого счетчика

По сравнению с описанным алгоритмом инкрементирования $i$ -го разряда избыточного представления здесь мы должны учесть работу со списочной частью и обновить прямые указатели.

rmIncRootCount(i,p)
  if (rootCount[i].Value == 1) or (rootCount[i].Value == 2)
    if rootCount[rootCount[i].forwardPointer].Value == 3
      fixRootCount(rootCount[i].forwardPointer);
  if rootCount[i].Value == 3
    fixRootCount(i)
  insertTree(i, p)
  rootCount[i].Value = rootCount[i].Value + 1
  updateForwardPointer(i)
  if rootCount[i].Value == 3
    fixRootCount(i)

Удаление дерева из кучи

Процедура удаления дерева из кучи подразумевает наличие в куче этого дерева. Пусть удаляемое дерево имеет ранг $i$ . Тогда значение $i$ -го разряда избыточного корневого представления не равно нулю. То есть уменьшение этого значения на единицу не испортит регулярности представления и не потребует обновления каких-либо указателей. Необходимо лишь соответствующим образом обработать списочную часть.

delete(i, p):
  deleteTree(i, p)
  rootCount[i].Value = rootCount[i].Value - 1

Нахождение дерева с минимальным ключом в корне $\mathrm{minKey()}$

minKey()
  minP = NULL
  for i = 0 to maxRank:
    p1 = minKeyNodeRoot(rootCount[i].listPointer)
    if getKey(p1) < getKey(minP):
      minP = p1
  return minP

Счетчик нарушений

Заметим, что счетчик нарушений очень похож на корневой счетчик выше, но в отличие от второго:

Нас теперь интересует не само число, а только значения разрядов.
Операция фиксации тесно связана с толстой кучей.

Значение $i$ -го разряда для счетчика нарушений интерпретируется как количество неправильных узлов ранга $i$ , а его списочная часть — это указатели на неправильные узлы ранга $i$ .

Счетчик нарушений состоит из расширенного избыточного двоичного представления и набора списочных элементов.

Счетчик нарушений представлен саморасширяющимся массивом, элементы которого состоят из четырех полей:

$countViolation[i].Value$ — количество неправильных узлов ранга $i$ в куче.
$countViolation[i].forvardPointer$ — прямой указатель $i$ -го разряда
$countViolation[i].firstViolation$ — указатель на неправильный узел ранга $i$
$countViolation[i].secondViolation$ — указатель на неправильный узел ранга $i$

Утверждение (о счетчике нарушений):

из определения счетчика нарушений следует:

Наличие счетчика нарушений позволяет иметь доступ к любому неправильному узлу ранга $i$ за время $O(1)$ .
Уменьшение ключа у элемента ранга $i$ соответствует операции инкрементирования $i$ -го разряда счетчика нарушений (естественно, лишь в случае, когда новое значение ключа у изменяемого узла становится меньше значения ключа его родителя).
Операции инкрементирования и декрементирования $i$ -го разряда осуществляются за время $O(1)$ .

Для инициализации нового звена в счетчике нарушений необходимо лишь занулить его значение в новом разряде. Делается это только тогда, когда мы вводим в кучу новое дерево ранга $maxRank + 1$ . Это первый момент появления в куче узла ранга $maxRank + 1$ . Для тех нарушений, которые могут возникнуть в узлах ранга меньше либо равного $maxRank + 1$ , соответствующие разряды счетчика нарушений уже инициализированы, а узлов большего ранга в куче пока нет.

Основные операции

Рассмотрим операции, которые можно производить с толстой кучей. Время работы основных операций указано в таблице:


Операция	Время работы
$\mathrm{makeHeap}$	$O(1)$
$\mathrm{findMin}$	$O(1)$
$\mathrm{insert(key)}$	$O(1)$
$\mathrm{decreaseKey}$	$O(1)$
$\mathrm{deleteMin}$	$O(\log(n))$
$\mathrm{delete}$	$O(\log(n))$
$\mathrm{meld(h1, h2)}$	$O(\log(n))$

makeHeap

Заключается в инициализации счетчиков.

findMin

Возвращает указатель на минимальный элемент.

insert(key)

Чтобы выполнить эту операцию, делаем новый элемент отдельным деревом и выполняем процедуру вставки нового элемента ранга $0$ в корневой счетчик. После этого, если необходимо, корректируем значение указателя на минимальный элемент.

decreaseKey

Чтобы выполнить эту операцию, поступим следующим образом. Пусть $x$ — узел, на который указывает указатель $p$ . Вычитаем $\delta$ из ключа узла $x$ . Если новый ключ $x$ меньше минимального ключа кучи $H$ , обмениваем ключ элемента $p$ с ключом минимального элемента. Новых нарушений операция не создаст. Пусть $r$ — ранг $x$ . Если $x$ — нарушаемый узел, добавляем $x$ как новое $r$ -ранговое нарушение инкрементированием $r$ -й цифры $d_r$ счетчика нарушений.

deleteMin

Удаляем поддерево с корнем в минимальном узле из леса. Минимальность этого элемента гарантирует нам, что среди его детей нарушений порядка кучи не было. То есть нет необходимости работать со счетчиком нарушений. Затем вставляем в кучу все деревья с корнями, расположенными в детях удаляемого узла. Очевидно, что новый минимальный ключ — либо в корне дерева леса, либо в нарушенном узле. Выполняем поиск нового минимального элемента среди корней деревьев и нарушенных узлов. Если минимальный элемент оказался в нарушенном узле, то обмениваем его с элементом, хранимым в корне этого дерева, корректируя корневой счетчик, если это необходимо. После замены новый минимум — в корне дерева леса. Этот корень будет новым минимальным узлом.

delete

Выполняем $\mathrm{decreaseKey}$ а затем $\mathrm{deleteMin}$ .

meld(h1, h2)

Первый шаг — фиксируются все нарушения в куче с меньшим максимальным рангом (разрывая связь произвольно). Не уменьшая общности, считаем, что эта куча — $р2$ . Пройти по счетчику нарушений $p2$ от младшей цифры к старшей, пропуская цифры со значением $0$ . Для $i$ -й цифры $d_i != 0$ делаем операцию фиксирования на каждой цифре, показываемой прямым указателем $d_i$ , если эта цифра имеет значение $2$ . Затем, если $d_i = 2$ , фиксируем $d_i$ . Если $d_i = 1$ , преобразуем это $i$ -ранговое нарушение в $(i+1)$ -ранговое нарушение, как при фиксировании, используя $i$ -рангового брата нарушенного узла вместо (несуществующего) другого $i$ -рангового нарушения. Как только $h2$ не будет содержать каких-либо нарушений, нужно вставить корни из корневого счетчика $h2$ в корневой счетчик $h1$ инкрементированием соответствующих цифр. Если минимальный узел $h2$ содержит меньший ключ, чем минимальный узел $h1$ , следует установить новым минимальным узлом $h1$ минимальный узел $h2$ . Затем нужно вернуть модифицированную кучу $h1$ в качестве результата $\mathrm{meld}$ .

deleteViolation

Для освобождения кучи от нарушений достаточно выполнить следующий псевдокод:

deleteViolation(h2):
  for i = 0 to h2.maxRank
    if countViolation[i].Value == 2
      fixCountViolation(i)
  for i = 0 to h2.maxRank
    if countViolation[i].Value == 1
      incCountViolation(i, searchBrother(countViolation[i].rmFirstviolation))
      fixCountViolation(i)

Источники

Толстая куча на избыточном счётчике

Толстое дерево

Толстые кучи

Структура узла

Структура кучи

Избыточное представление чисел

Фиксация цифры

Инкремент

Декремент

Корневой счетчик

Инициализация

Обновление прямого указателя

Корректировка при вставке

Корректировка при удалении

Связывание трех деревьев в одно

Значение ключа элемента по указателю

Узел с минимальным ключом

Операция фиксации

Инкрементирование i-го разряда корневого счетчика

Удаление дерева из кучи

Нахождение дерева с минимальным ключом в корне minKey()\mathrm{minKey()}

Счетчик нарушений

Основные операции

makeHeap

findMin

insert(key)

decreaseKey

deleteMin

delete

meld(h1, h2)

deleteViolation

Источники

Навигация

Поиск

Нахождение дерева с минимальным ключом в корне $\mathrm{minKey()}$