Деревья Эйлерова обхода

Введение

Для решения задачи о динамической связности (англ.dynamic connectivity problem) требуется выполнение следующих операций:

• $\mathrm{link(u, w)}$ — добавить ребро (u, w) (при условии, что вершины u w принадлежат разным деревьям),
• $\mathrm{cut(u, w)}$ — разрезать ребро (u, w) (при условии, что ребро (u, w) принадлежит дереву),
• $\mathrm{isConnected(u, w)}$ — определить принадлежат ли вершины u и w одной компоненте связности.

Дерево эйлерова обхода (англ.Euler tour tree) — способ представления динамического дерева, позволяющий выполнять указанные операции за $O(\log n)$.

Представление деревьев в виде эйлерова графа

Пример дерева

Соответствующий эйлеров граф

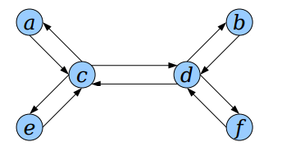
Для представления дерева в виде эйлерового графа заменим каждое ребро [math]\{u, v\} \[/math] дерева на два ребра $(u, v)$ и $(v, u)$.

Получившийся ориентированный граф будет эйлеровым согласно критерию.

Свойство эйлерова обхода

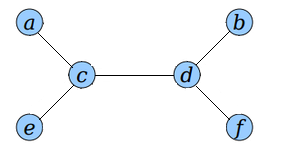
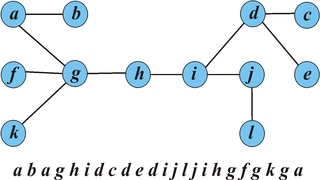
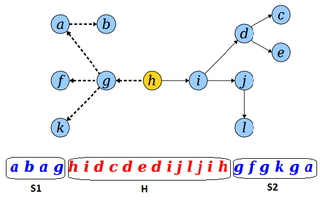
Представим дерево в виде последовательности вершин, посещеннных в порядке эйлерова обхода с корнем в вершине $a$.

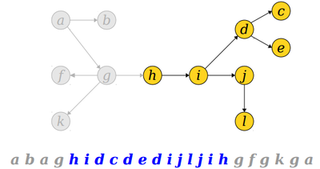
При этом последовательность вершин между первым и последним вхождением вершины $h$ дает эйлеров обход поддерева с корнем $h$.

Операции

Изменение корня дерева (переподвешивание)

Дано дерево с корнем в вершине $a$. Требуется переподвесить его к вершине $h$.

Для переподвешивания (англ. rerooting) необходимо:

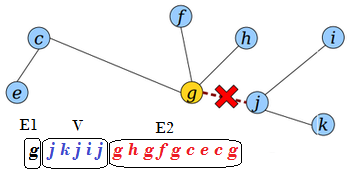
• Разбить эйлеров обход на три части $S1$, $H$, и $S2$, где $H$ состоит из вершин между первым и последним вхождением нового корня $h$.
• Удалить первую вершину в $S1$.
• Соединить в следующем порядке: $H$, $S2$, $S1$.
• Добавить $\{h\}$ в конец последовательности.

В результате получим:

Добавление ребра

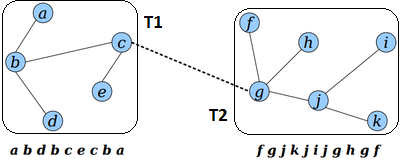
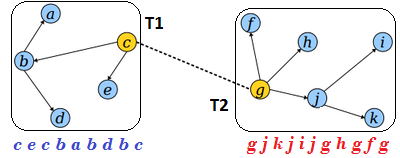
Для связывания деревьев $T1$ и $T2$, где $c\in T1\ $, а [math]g\in T2\[/math] добавлением ребра [math]\{c, g\} \[/math] необходимо:

• Переподвесить дерево $T1$ к вершине $c$.
• Переподвесить дерево $T2$ к вершине $g$.
• Соединить получившиеся эйлеровы обходы.
• Добавить $\{c\}$ в конец последовательности.

В результате получим:

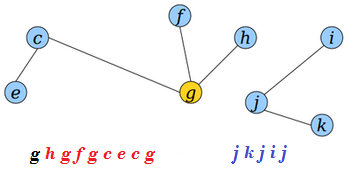
Разрезание ребра

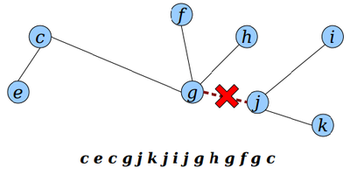
Для разбиения дерева на два поддерева путем разрезания ребра [math]\{g, j\} \[/math] (если оно существует) необходимо:

• Переподвесить дерево к вершине $g$.
• Разделить дерево на части $E1, V, E2$, где $V$ отрезок между первым и последним вхождением вершины $j$.
• Эйлеров обход первого поддерева образуется соединением $E1$ и $E2$, с удалением повторного $\{g\}$ в месте их соединения.
• Эйлеров обход второго поддерева образует $V$.

В результате получим:

Реализация структуры

Задача:

Определить структуру данных для хранения эйлеровых обходов деревьев для наиболее эффективного выполнения указанных операций.

При представлении деревьев в виде их эйлерова обхода выполнение каждой операции $mathrm{link}$ и $mathrm{cut}$ сводится к $O(1)$ соединений и разбиений отрезков в последовательности вершин эйлерова обхода.

Рассмотрим следующие структуры данных для определения времени выполнения разбиения и соединения последовательностей, а также определение принадлежности вершин одной компоненте связности.

Связные списки

Each split or concatenate takes time O(1). Каждое разбиение и соединение последовательностей требует О(1) времени.
The first and last copy of a node can be identified in time O(1).Определение первого и последнего вхождения вершины в последовательность происходит за О(1).
A new copy of a node can be appended to the end of the sequence in time O(1).Новая копия вершины может быть добавлена в конец последовательности за О(1).
A redundant copy of a node can be deleted in time O(1).Лишняя копия вершины может быть удалена за О(1).
Everything sounds great!
Question: How do you test for connectivity?

Euler tours give a simple, flexible encoding of tree structures.
Using doubly-linked lists, concatenation and splits take time O(1) each, but testing connectivity takes time Θ(n) in the worst-case.
Can we do better? Используя двойные связные списки добавление и разрезание ребра может быть проведено за время О(1), но определение принадлежности вершин одной компоненте связности занимает Θ(n) в худшем случае.

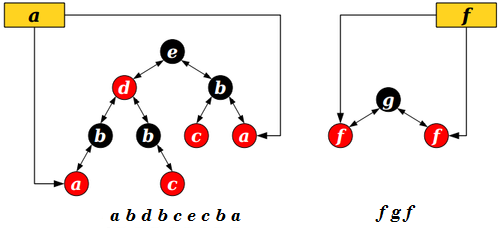
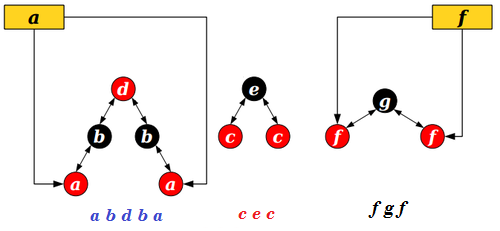
Balanced Trees

Claim: It is possible to represent sequences of elements balanced binary trees.

These are not binary search trees. We're using the shape of a red/black tree to ensure balance.

Observation 1: Can still store pointers to the first and last occurrence of each tree node.

Observation 2: If nodes store pointers to their parents, can answer is-connected(u, v) in time O(log n) by seeing if u and v are in the same tree.

Observation 3: Red/black trees can be split and joined in time O(log n) each.

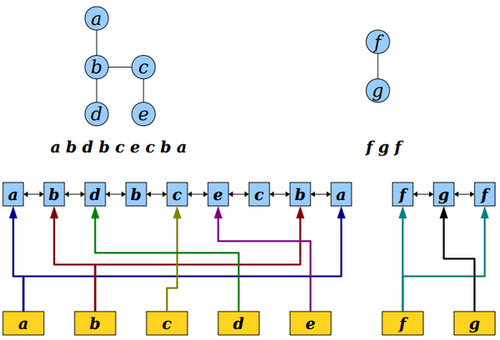
The data structure:
Represent each tree as an Euler tour.
Store those sequences as balanced binary trees.
Each node in the original forest stores a pointer to its first and last occurrence.
Each node in the balanced trees stores a pointer to its parent.
link, cut, and is-connected queries take time only O(log n) each.

Сравнительная табличка

Похожие структуры

Про link-cut trees