Теорема о декомпозиционном барьере
Версия от 17:05, 5 января 2017; Shersh (обсуждение | вклад)
| Теорема (о декомпозиционном барьере): |
Существуют положительные вещественные числа и , такие что для любых натуральных и , удовлетворяющих неравенствам , существует сеть с вершинами и ребрами, такая что для любого максимального потока в , любая его остаточная декомпозиция должна содержать слагаемых (т.е. путей или циклов), причем каждый из путей (циклов) в декомпозиции должен иметь длину . |
| Доказательство: |
|
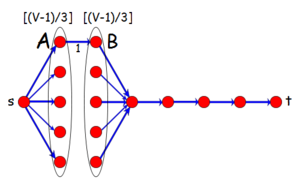
Возьмем и . Константа выбрана таким образом, чтобы между и было ребер, а константа выбрана такой, потому что в рассматриваемой сети нельзя провести большее количество ребер. Чтобы получить искомую сеть, строится сеть, изображенная на рисунке, после чего добавляется нужное количество ребер из в . Пропускные способности ребер из в равны , остальных — (или просто достаточно большое число, например, ).
Теперь докажем саму теорему:
|
Следствие: Алгоритмы, которые могут выписать декомпозицию потока вместе с поиском самого потока (Алгоритм Диница, Алгоритм Эдмондса-Карпа, Алгоритм Форда-Фалкерсона и подобные) не могут работать быстрее чем за , так как декомпозиция может быть сама по себе большой.