Материал из Викиконспекты
| Определение: |
| Гиперграфом (англ. hypergraph) [math]H[/math] называют такую пару [math]H = (X, E)[/math] , где [math]X - [/math] множество вершин, а [math]E -[/math] семейство подмножеств [math]X[/math] , называемых гиперребрами (англ. hyperedges) |
Обычные графы, у которых ребра могут соединять только две вершины, являются частным случаем гиперграфа, у которых все гиперребра содержат только две вершины.
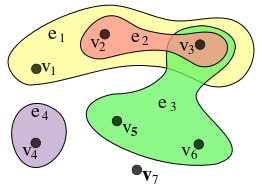
Рис. 1: Гиперграф с множеством вершин
[math]V = \{ v_1, v_2, v_3, v_4, v_5, v_6, v_7 \}[/math] и гиперребрами
[math]E = \{ \{ v_1, v_2, v_3 \} , \{ v_2, v_3 \} , \{ v_3, v_5, v_6 \} , \{ v_4 \} \}[/math]
| Определение: |
Путем (англ. path) между двумя гиперребрами [math]e_i[/math] и [math]e_j[/math] гиперграфа [math]H[/math] называется последовательность гиперребер [math]e_{u_1}, e_{u_2} , \ldots ,e_{u_k}[/math] таких что :
- [math]e_{u_1} = e_i [/math] и [math]e_{u_k} = e_j[/math]
- [math]\forall v: 1 \leqslant v \leqslant k-1, e_v \cap e_{v+1} \ne \emptyset[/math]
|
| Определение: |
| Гиперграф [math]H[/math] называется связным (англ. connected) тогда и только тогда, когда существует путь между каждой парой гиперребер. |
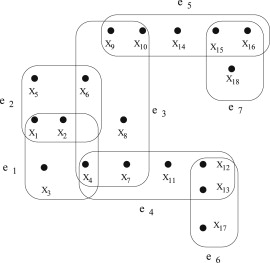
Рис. 2: Связный гиперграф
Пусть [math]E - [/math] набор гиперребер, [math]e_1[/math] и [math]e_2 - [/math] элементы [math]E[/math] и [math]q = e_1 \cap e_2[/math].
| Определение: |
| [math]q[/math] называется сочленением (англ. articulation) [math]E[/math] , если при его удалении из всех гиперребер [math]E[/math], множество разрывается. |
На рис.2 [math]q = e_4 \cap e_6 = \{ x_{12}, x_{13}\}[/math] является сочленением [math]E[/math].
Матрица инцидентности
Пусть дан гиперграф [math]H = (X, E)[/math] , где [math] X = \{ x_1, x_2, \ldots , x_n \}[/math] и [math] E = \{ e_1, e_2, \ldots , e_m \}[/math]. Любой гиперграф может задаваться матрицей инцидентности (смотри матрицу инцидентности в обычном графе) [math]A = (a_{ij}) [/math] размером [math] n \times m[/math], где
[math] a_{ij} = \left \{
\begin{array}{ll}
0 & x_i \in e_j \\
1 & \mathrm{otherwise}
\end{array}
\right.
[/math]
Так например, для гиперграфа на рис.1 мы можем построить матрицу инцидентности по таблице отношения принодлежности вершины к гиперребру:
|
|
[math]e_1[/math]
|
[math]e_2[/math]
|
[math]e_3[/math]
|
[math]e_4[/math]
|
| [math]v_1[/math]
|
✓ |
|
|
|
| [math]v_2[/math]
|
✓ |
✓ |
|
|
| [math]v_3[/math]
|
✓ |
✓ |
✓ |
|
| [math]v_4[/math]
|
|
|
|
✓
|
| [math]v_5[/math]
|
|
|
✓ |
|
| [math]v_6[/math]
|
|
|
✓ |
|
| [math]v_7[/math]
|
|
|
|
|
[math] A = [/math]
[math]\begin{pmatrix}
1 & 0 & 0 & 0\\
1 & 1 & 0 & 0\\
1 & 1 & 1 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 0\\
\end{pmatrix}[/math]
Ацикличность в гиперграфе
| Определение: |
| Простым циклом длины [math]s[/math] в гиперграфе [math]H = (V, E)[/math] называется последовательность [math]( A_0, v_0, A_1, \ldots , A_{s - 1}, v_{s - 1}, A_s)[/math] , где [math]A_0 , \ldots , A_{s - 1} -[/math] различные ребра [math]H[/math] , ребро [math]A_s[/math] совпадает с [math]A_0[/math] , а [math]v_0, \ldots , v_{s - 1} -[/math] различные вершины [math]H[/math] , причем [math]v_i \in A_i \cap A_{i+1}[/math] для всех [math] i = 0, \ldots , s - 1[/math]. |
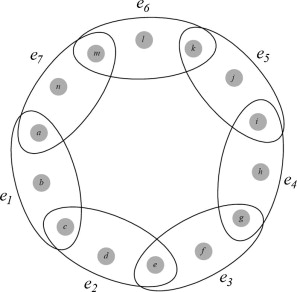
Рис. 3: Простейший случай цикла в гиперграфе
Универсальным способом задания гиперграфа является кенигово представление.
| Определение: |
| Кенигово представление гиперграфа [math] H = (V, E) -[/math] обыкновенный двудольный граф [math]K(H)[/math] , отражающий отношение инцидентности различных элементов гиперграфа, с множеством вершин [math]V \cup E [/math] и долями [math]V, E[/math]. |
Первым, кто дал определение ацикличности гипергафа является Клауд Берж:
| Теорема: |
Гиперграф [math]H[/math] не содержит циклов в том случае, если его кенигово представление [math]-[/math] ацикличный граф, сожержит в противном случае. |
Таким образом, если у нас есть цикл в графе кенигова представления, значит и сам гиперграф имеет цикл.
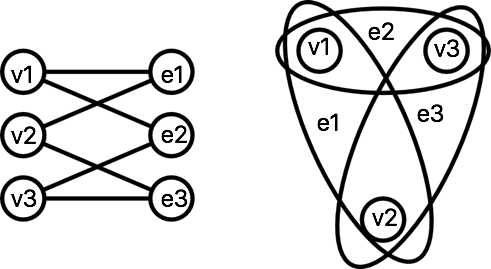
Рис. 4: Пример гиперграфа, содержащего цикл
См. такжеИсточники информации



