Персистентная приоритетная очередь
Персистентная приоритетная очередь (англ. persistent priority queue) — приоритетная очередь, реализующая персистентность, то есть позволяющая получить доступ ко всем своим предыдущим версиям.
Реализация с помощью дерева отрезков
Идея
Известно, что на основе дерева отрезков можно построить полностью персистентную структуру данных. Поэтому используем его, модифицируя операцию изменения на случай вставки и удаления элементов очереди.
Реализация
Будем хранить явные указатели на дочерние элементы. Тогда структура узла дерева примет следующий вид:
struct Node: Node left Node right T key Node(val : T) //конструктор для листов Node(leftChild : Node, rightChild : Node) //конструктор для узлов(присваивает полю key минимальное среди leftChild и rightChild)
Реализуем следующие функции:
- — построение дерева,
- — вставка нового элемента очереди,
- — удаление минимального элемента очереди,
- — слияние.
Каждая функция возвращает корень нового дерева, которое потом можно будет снова изменять. При реализации можно хранить отдельный массив корней деревьев и при каждом новом изменении какой-либо из версий добавлять измененную в конец массива.
build
Дерево будет построено фиксированного размера. Стоит отметить, что при создании нескольких деревьев необходимо придерживаться одного максимального размера. Асимптотика построения дерева отрезков составит .
Node build(left : uint, right : uint):
if left == right
return Node()
uint mid = (left + right) / 2
return Node(build(left, mid), build(mid + 1, right))
insert
Вставлять новое значение мы будем в любой пустой лист. Лист считается пустым, если его значение равно . При этом не стоит забывать, что те узлы, которые подвергаются изменению, нужно сначала скопировать, а потом вставить новый на основе скопированного для сохранения предыдущих состояний очереди. Запрос вставки нового ключа создает новых вершин и время его работы .
Node insert(currentNode : Node, newVal : T): if currentNode.left == null and currentNode.right == null and currentNode.val != //если лист занят return null if currentNode.left == null and currentNode.right == null and currentNode.val == //если лист свободен return Node(newVal) Node temp = insert(currentNode.left, newVal) if temp == null temp = insert(currentNode.right, newVal) if temp == null return null else return Node(currentNode.left, y) else return Node(y, currentNode.right)
extractMin
Учитывая тот факт, что корень дерева содержит ключ минимального элемента, можно найти путь к листу, содержащему этот элемент, и удалить его. Аналогично вставке, не стоит забывать о сохранении предыдущих состояний очереди. Вызов функции должен производиться указанием в качестве аргументов корня дерева и значения в корне дерева. Запрос удаления минимального ключа создает новых вершин.
Node extractMin(currentNode : Node, delVal : T):
if currentNode.left == null and currentNode.right == null and currentNode.val == delVal
return Node()
if currentNode.left.val == delVal:
return Node(extractMin(currentNode.left, delVal), currentNode.right)
else
return Node(currentNode.left, extractMin(currentNode.right, delVal))
merge
Слияние двух деревьев будет производить с помощью конструктора структуры. Поэтому оно выполняется за .
Node merge(leftTree : Node, rightTree : Node) return Node(leftTree, rightTree)
Реализация с помощью левосторонней кучи
Реализуем приоритетную очередь на левосторонней куче. Т.к. в левосторонней куче нигде не делается уничтожающих присваиваний, то можно её преобразовать в персистентную приоритетную очередь.
Будем хранить структуру:
struct LeftistHeap: LeftistHeap left LeftistHeap right T key int dist LeftistHeap(leftChild : LeftistHeap, rightChild : LeftistHeap, val : T)
Приведём реализацию конструктора:
LeftistHeap(leftChild : LeftistHeap, rightChild : LeftistHeap, val : T):
key = val
if leftChild.dist > rightChild.dist
left = leftChild
right = rightChild
else
left = rightChild
right = leftChild
dist = min(left.dist, right.dist) + 1
Поддерживаемые операции
Все операции практически (кроме ) аналогичны операциям с левосторонней кучей, только каждая из них возвращает корень измененной кучи. В частности возвращает пару из извлеченной вершины и измененной кучи.
примет следующий вид:
LeftistHeap merge(x : LeftistHeap, y : LeftistHeap): if x == : return y if y == : return x if y.key >= x.key: z = LeftistHeap(x.left, merge(x.right, y), x.key) else z = LeftistHeap(y.left, merge(y.right, x), y.key) return z
Реализация с помощью биномиальной кучи
Возьмем биномиальную кучу и реализуем ее на односвязных списках.
Для этого будем хранить список корней в порядке возрастания ранга, а детей будем хранить по убыванию ранга. Каждый родитель будет знать ребенка с большим рангом, который является головой списка детей, но ребенок не будет знать родителя. Т.к. дочерний элемент не знает о своем родителе, то можно объединять деревья, сохраняя персистентность данной структуры.
Структура кучи
Каждый узел в персистентной биномиальной куче представляется набором полей:
- — ключ (вес) элемента,
- — указатель на следующий элемент,
- — указатель на ребенка с большим рангом,
- — степень узла (количество дочерних узлов данного узла).
Доступ к куче осуществляется ссылкой на первый корень в списке корней.
Операции
getMinimum
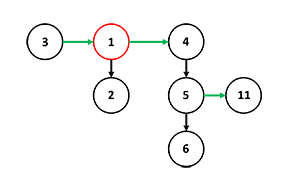
Для нахождения минимального элемента необходимо пройти по списку корней дерева. Можно это сделать за , т.к. список корней содержит не более элементов. На рисунке это корень второго дерева в куче.
merge
Проходим по корневым спискам и создаем новый, объединяя деревья одинакового ранга.
Вспомогательная функция объединят в одно деревья одинакового ранга. Для этого мы создаём два новых узла, один из которых — новый корень, другой из них — видоизмененный корень одного из деревьев.
PersistentBinomialHeap mergeTree(t1 : PersistentBinomialHeap, t2 : PersistentBinomialHeap):
newRoot = PersistentBinomialHeap()
tmp = PersistentBinomialHeap()
newRoot.child = tmp
newRoot.degree = t1.degree + t2.degree
if (t1.key < t2.key)
tmp = PersistentBinomialHeap(t2) //создаем новый узел путем копирования старого с помощью конструктора
tmp.next = t1.child
newRoot.key = t1.key
else
tmp = PersistentBinomialHeap(t1)
tmp.next = t2.child
newRoot.key = t2.key
return newRoot
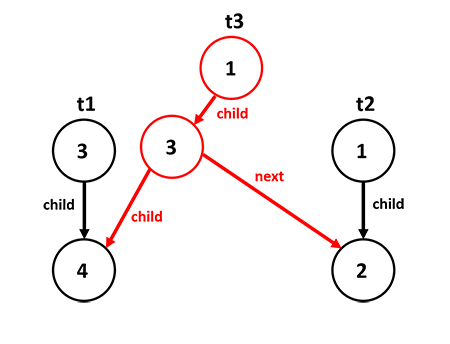
Процесс слияния двух деревьев показан на рисунке. Первоначально было два дерева и (на рисунке выделены черным). Затем их слили, появились два новых узла, которые обращаются по прежнему к старым поддеревьям (выделено красным).
Проход по корневым спискам выполнится за , объединение деревьев выполняется за . Тогда работает за .
insert
Общий принцип вставки нового элемента схож с принципом вставки в эфемерную биномиальную кучу. Создаем кучу с деревом ранга , в котором будет единственный элемент — тот самый, который нам нужно вставить. И затем сливаем две кучи в одну.
Есть два случая слияния:
- Минимальный ранг дерева в куче равен нулю. Тогда сливаем две кучи в одну с помощью . Время работы .
- Минимальный ранг дерева в куче отличен от нуля. Тогда присоединяем к созданной куче ту, в которую нужно добавить элемент. Время работы .
Тогда амортизационная стоимость одной операции составляет .
PersistentBinomialHeap insert(heap : PersistentBinomialHeap, newVal : T):
newRoot = PersistentBinomialHeap(newVal)
if heap.degree == newRoot.degree:
return mergeTree(newRoot, heap)
else
newRoot.next = heap
return newRoot
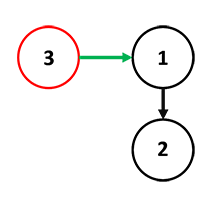
Пример работы.
extractMinimum
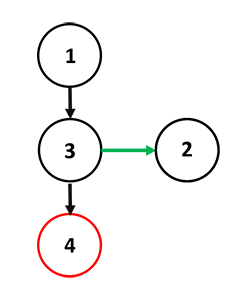
Работает так же как и в эфемерной биномиальной куче. Проходим по списку корней и находим вершину с минимальным ключом. Затем извлекаем дерево, которое хранит минимальный ключ. Сортируем детей в дереве с минимальным ключом по возрастанию ранга. Сливаем две кучи.
function extractMinimum(t : PersistentBinomialHeap):
tmp = t
minimum = t
while tmp != null
if minimum.key > tmp.key
min = tmp
tmp = tmp.next;
tmp = t
H = PersistentBinomialHeap()
tmpNewRoot = H
while tmp != null
if tmp.next == min
tmpNewRoot = PersistentBinomialHeap(tmp)
tmpNewRoot.next = tmp.next.next
else
tmpNewRoot = PersistentBinomialHeap(tmp)
tmpNewRoot = tmpNewRoot.next
//расставляем детей в удаленном дереве в возрастающем порядке с помощью вспомогательного массива nodes
H' = PersistentBinomialHeap()
tmp = min.child
x = 0
while tmp != null
nodes[x] = tmp
tmp = tmp.next
x = x + 1
tmp = H'
for i = x - 1 downto 0
tmp.next = PersistentBinomialHeap(nodes[x])
tmp = tmp.next
return (merge(H.next, H'.next), min.key)
Функция возвращает минимальный ключ и новую кучу после извлечения минимума. Работает за .