Проблема четырёх красок
Краткая история
Раскрашивая географическую карту естественно пользоваться по возможности меньшим количеством цветов, однако так, чтобы две страны, имеющие общую часть границы (не только общую точку), были окрашены по-разному. В году Френсис Гутри, составляя карту графств Англии, обратил внимание, что для такой цели вполне хватает четырех красок. Его брат, Фредерик, сообщил об этом наблюдении известному математику О. Де Моргану, а тот – математической общественности. Точная формулировка гипотезы опубликована А. Кэли в году. Первое доказательство появилось год спустя и принадлежало В. Кемпе. Одиннадцать лет спустя П. Хивуд обнаружил в нем ошибку (Однако из доказательства Хивуд понял, что пяти красок действительно достаточно). За первым ошибочным доказательством последовало множество других. До середины XX века, хотя проблемой четырех красок занимались многие выдающиеся математики, положение с доказательством изменилось несущественно: идеи Дж. Д. Биркгофа позволили П. Франклину в году доказать гипотезу для карты с не более чем странами. Позже это число было увеличено до . В году доказательство гипотезы четырех красок было наконец получено К. Аппелем и У. Хакеном и опубликовано в двух статьях [1]. Значительную часть рутинных проверок выполнил компьютер, и это революционное нововведение в сложившуюся практику дедуктивных рассуждений в чистой математике служит основанием для некоторого естественного скептицизма по отношению к данному доказательству и по сей день.
Формулировка проблемы
| Теорема (Проблема четырех красок): |
Теорема о четырёх красках — утверждение о том, что всякую карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. Под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются. |
Проблема четырех красок кажется на первый взгляд изолированной задачей, мало связанной с другими разделами математики и практическими задачами. На самом деле это не так. Известно более ее переформулировок, которые связывают эту проблему с задачами алгебры, статистической механики и задачами планирования.
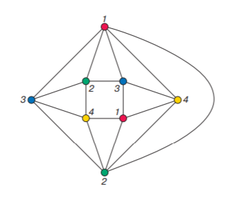
Поэтому для доказательства начнем с того, что заменим задачу раскраски плоской карты на эквивалентную ей проблему. Выберем столицу у каждой страны (то есть выберем по одной внутренней точке в каждой из стран) и соединим дугами столицы стран, имеющих общий сегмент границы. В результате получится планарный граф. Тогда следующая теорема эквивалентна теореме выше:
| Теорема (Хроматическое число планарного графа): |
Хроматическое число планарного графа не превосходит . |
Доказательство Аппеля и Хакена, в целом хотя и принято математическим сообществом, но, как было сказано выше, вызывает до сих пор определенный скептицизм. Дело в том, что даже сами авторы доказательства пишут следующее:
"Читатель должен разобраться в страницах текста и диаграмм, страницах с почти дополнительными диаграммами, страницами микрофишей, содержащими еще диаграммы, а также тысячи отдельных проверок утверждений, сделанных в леммах основного текста. Вдобавок читатель узнает, что проверка некоторых фактов потребовала часов компьютерного времени, а при проверке вручную потребовалось бы гораздо больше. Статьи устрашающи по стилю и длине, и немногие математики прочли их сколько-нибудь подробно"
Говоря прямо, компьютерную часть доказательства почти невозможно проверить вручную, а традиционная часть доказательства длинна и сложна настолько, что ее никто целиком и не проверял. Некоторое время назад появилось новое доказательство [2], причем та часть, которая выполнена не на компьютере, уже поддается проверке. Однако компьютерная часть все еще остается скорее предметом веры.
Общие идеи доказательства
Очевидно, что мы не сможем рассмотреть доказательство целиком, но посмотрим на общие идеи, которые в нем используются.
Во-первых, если грани образованные нашим планарным графом не триангуляция, то есть имеют не ровно три ребра у их границ, мы можем добавлять ребра без внедрения новых вершин до тех пор, пока все грани не станут триангулированными. Если эта триангуляция графа является раскрашиваемой в и менее цветов, то и исходный граф раскрашиваем так же (так как удаление ребер не увеличивает хроматическое число). Поэтому достаточно доказать теорему четырех цветов для триангулированных графов, чтобы доказать ее для всех плоских графов, и без потери общности мы предполагаем, что граф триангулирован.
Для дальнейших рассуждений нам понадобится следующее утверждение:
| Утверждение: |
Для триангулированного графа , где — количество вершин степени , а — максимальная степень вершины в графе. |
| Так как граф триангулирован, то , где — количество ребер, а — количество граней. Из формулы Эйлера |
Из данного утверждения следует, что в графе существует вершина степени .
Вернемся к доказательству нашей теоремы. Будем пытаться доказать от противного. Пусть у нас существует граф, который требует хотя бы цветов для раскраски. Среди всех таких графов существует минимальный, то есть такой, что удаление любой вершины из него делает его -раскрашиваемым. Тогда в таком графе не может быть вершины степени , так как иначе мы может просто удалить ее из графа, раскрасить полученный граф в цвета, вернуть удаленную вершину и покрасить ее в один из цветов, не занятых соседями. Аналогично теореме Хивуда доказывается, что удалив вершину степени также всегда можно раскрасить граф в цвета. Следовательно, и таких вершин в искомом графе нет. Для вершины степени Кемпе попытался доказать аналогичное утверждение, но это утверждение и было опровергнуто Хивудом.
На этом этапе мы и натыкаемся на самую сложную часть доказательства. Имея дело со случаем вершины степени , требуются более сложные операции, чем удаление вершины. Тогда вместо вершины будем рассматривать связанный подграф из нескольких вершин (назовем его конфигурацией). Тогда для некоторых случаев, как и прежде, достаточно продемонстрировать, что если при удалении конфигурации граф -раскрашиваемый, то окраска может быть изменена таким образом, что при возвращении конфигурации граф также можно раскрасить в цвета. Конфигурации для которых это возможно назовем сводимыми. Например, конфигурация состоящая из вершины степени является сводимой (было доказано выше). Неизбежной конфигурацией назовем такое множество конфигураций, что хотя бы одна из конфигураций этого множества обязана быть в нашем графе.
Если нам удастся найти какую-то неизбежную конфигурацию и доказать, что с ней граф все равно -раскрашиваем, доказательство будет завершено. Основным методом, используемым, чтобы обнаружить такой набор, является метод разгрузки
Приведем пример нахождения неизбежной конфигурации:
| Утверждение: |
В планарном графе есть вершина степени или конфигурация состоящая из вершин степени или из вершины степени и степени |
| Присвоим каждой вершине некую величину — груз . Предположим что наше утверждение неверно. Следовательно, в графе нет вершин степени . Тогда положительный груз есть только у вершин степени (и он равен единице), у вершин степени груз , а у всех остальных он отрицательный. По доказанному выше утверждению, мы знаем что сумма грузов по всем вершинам . Значит вершины степени должны компенсировать все отрицательные грузы других вершин. Пусть каждая такая вершина отдает по своего груза соседям. Тогда у всех вершин степени и груз останется равен (помним что вершины степени не смежны с вершинами степени по предположению). Рассмотрим все остальные вершины. Так как мы проводим доказательство для триангулированных графов, то у вершины степени не может быть больше чем соседей степени . Однако для , следовательно, сумма грузов отрицательна. Получено противоречие. |
Выше мы получили неизбежную конфигурацию, состоящую из небольшого количество элементов. Подобными действиями Аппель и Хакен провели операций разгрузки и получили неизбежную конфигурацию из конфигураций. Некоторые из них являются сводимыми, доказательством раскрашиваемости остальных и занимался компьютер.