Мультиплексор и демультиплексор
| Определение: |
| Мультиплексор (англ. multiplexer, или mux) - логическая схема, которая имеет $2^n + n$ входов и один выход. Обозначим входы как $x_0$, $x_1$, $\ldots$, $x_{2^n}$, $y_0$, $y_1$, $\ldots$, $y_{n-1}$. На выход подаётся то же, что подаётся на вход $x_i$, где $i$ - двоичное число, которое кодируется входами $y_0$, $y_1$, $\ldots$, $y_{n-1}$. |
| Определение: |
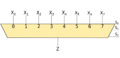
| Демультиплексор (англ. demultiplexer, или demux) - логическая схема, которая имеет $n + 1$ входов и $2^n$ выходов. На один из входов демультиплексора подаётся числа $a$, которое подаётся на $x_i$ выход, где $i$ - число, которое кодируется остальными $n$ входами, на остальные выходы подаются нули. |
Принцип работы мультиплексора
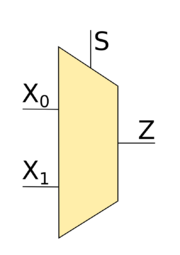
В качестве примера рассмотрим мультиплексор, которые имеет два входа $A$ и $B$, а также ещё вход $S$, значение которого задаёт, какой из входов $A$ или $B$ нужно подать на выход $Z$. Если на $S$ подавать $0$, то на $Z$ будет подаваться значение на входе $A$, если на $S$ подать $1$, то на выход $Z$ будет подаваться значение на входе $B$. Ниже представлена таблица истинности, которая иллюстрирует всевозможных состояния мультиплексора.
| $S$ | $X_0$ | $X_1$ | $Z$ |
|---|---|---|---|
| 0 | 0 | ? | 0 |
| 0 | 1 | ? | 1 |
| 1 | ? | 0 | 0 |
| 1 | ? | 1 | 1 |
Логическая схема мультиплексора
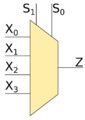
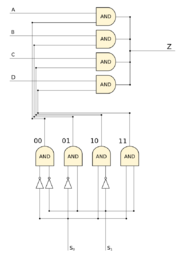
В качестве примера возьмём мультиплексор 4-to-1, у которого $2^2 + 2$ входа, и $1$ выход. Для того, чтобы обработать всевозможные варианты данных на входах $S_0$ и $S_1$ используются гейты $NOT$ и $AND$.
Основное преимущество мультиплексора в том, что его размер зависит линейно от количество входов. Построить такую схему не составит труда: Для начала надо перебрать всевозможные состояния входов $S_1$, $S_2$, $\ldots$, $S_n$. Сделать это можно рекурсивным способом: пусть мы смогли перебрать всевозможные состояния для первых $n-1$ входов. Тогда очевидно, что всевозможных вариантов сделать так - $2^{n-1}$. Давайте попробуем перебрать всевозможные варианты уже с $n$-ым входом. Пусть, что значение на входе $S_n$ равно $1$. Тогда достаточно поставить еще $2^{n-1}$ гейтов $AND$, и соединить эти гейты с проводами всевозможных состояний для $n-1$ компаратора. Путь значение на входе $S_n$ равно $0$. Тогда поставим всего один гейт $NOT$, и проделаем ту же самую операцию. Очевидно, что для того, чтобы присоединить $n$-ый вход мы использовали дополнительно $2^n$ гейтов $AND$ и $n$ гейтов $NOT$.