Теория Рамсея
Теория Рамсея — раздел математики, изучающий условия, при которых в произвольно формируемых математических объектах обязан появиться некоторый порядок.
Числа Рамсея
| Определение: |
| Клика (англ. clique) в неориентированном графе — подмножество вершин , такое что для любых двух вершин в существует ребро, их соединяющее. |
| Определение: |
| Число Рамсея (англ. Ramsey's number) — наименьшее из таких чисел , что при любой раскраске ребер полного графа на вершинах в два цвета найдется клика на вершинах с ребрами цвета или клика на вершинах с ребрами цвета . |
Часто определение для чисел Рамсея дается через задачу "о друзьях и незнакомцах"[1]. Пусть на вечеринке каждые два человека могут быть либо друзьями, либо незнакомцами, в общем виде задачи требуется найти, какое минимальное количество людей нужно взять, чтобы хотя бы человек были попарно знакомы, или хотя бы человек были попарно незнакомы. Если мы переформулируем данную задачу в терминах графов, то как раз получим определение числа Рамсея , представленное ранее.
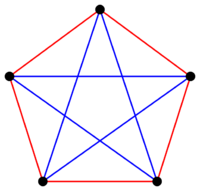
Чтобы получить лучшее представление природы чисел Рамсея, приведем пример. Докажем, что . Представим, что ребра раскрашены в два цвета: красный и синий. Возьмем вершину . Данной вершине, как и всем другим, инцидентны рёбер, тогда, согласно принципу Дирихле, хотя бы три из них одного цвета. Для определенности положим, что хотя бы ребра, соединяющие вершину с вершинами , , , синие. Если хотя бы одно из ребер , , синее, то в графе есть синий треугольник (полный граф на трёх вершинах), иначе, если они все красные, есть красный треугольник. Таким образом, . Чтобы доказать, что , предъявим такую раскраску графа , где нет клики на трех вершинах ни синего, ни красного цвета. Такая раскраска представлена на рисунке справа.
Теорема Рамсея. Оценки сверху
| Теорема (1, Теорема Рамсея): |
Для любых существует число , при этом , а также если числа и четные, то неравенство принимает вид . |
| Доказательство: |
|
Докажем с помощью метода математической индукции по . База: , так как граф, состоящий из одной вершины, можно считать полным графом любого цвета. Индукционный переход: Пусть и . Рассмотрим полный чёрно-белый граф из вершин. Возьмём произвольную вершину и обозначим через и множества, инцидентные в чёрном и белом подграфе соответственно. Так как в графе вершин, согласно принципу Дирихле, либо , либо . Пусть . Тогда либо в существует белый , что доказывает теорему, либо в есть чёрный , который вместе с образует чёрный , в этом случае теорема также доказана. Случай рассматривается аналогично. Предположим, и оба чётны. Положим и рассмотрим чёрно-белый граф из вершин. Если степень -й вершины в чёрном подграфе, то, согласно лемме о рукопожатиях, — чётно. Поскольку нечётно, должно существовать чётное . Не умаляя общности, положим, что чётно. Обозначим через и вершины, ,инцидентные вершине в чёрном и белом подграфах соответственно. Тогда и оба чётны. Согласно принципу Дирихле, либо , либо . Так как чётно, а нечётно, первое неравенство можно усилить, так что либо , либо . Предположим . Тогда либо подграф, порождённый множеством , содержит белый и доказательство завершено, либо он содержит чёрный , который вместе с вершиной образует чёрный . Случай рассматривается аналогично. |
| Утверждение (1): |
Для натуральных чисел выполняется равенство |
|
Очевидно, при или , как и соответствующие числа Рамсея. Индукцией по и при получаем |
Оценки снизу
| Теорема (2): |
Для любого натурального числа выполняется неравенство |
| Доказательство: |
|
Так как , достаточно рассмотреть случай . Зафиксируем множество различных помеченных вершин . Пусть — доля среди всех графов на вершинах тех графов, что содержат клику на вершинах. Всего графов на наших вершинах, очевидно (каждое из возможных рёбер можно провести или не провести). Посчитаем графы с кликой на вершинах следующим образом: существует способов выбрать вершин для клики в нашем множестве, после чего все рёбра между ними будем считать проведенными, а остальные ребра выбираются произвольно. Таким образом, каждый граф с кликой на вершинах будет посчитан, причём некоторые даже более одного раза. Количестве графов с кликой оказывается не более, чем . Следовательно,
Подставив в неравенство мы получаем при Предположим, что и разобьём все графы на вершинах на пары (граф и его дополнение) Так как , то существует пара, в которой ни , ни не содержат клики на вершинах. Рассмотрим раскраску рёбер в два цвета, в которой ребра цвета образуют граф . В такой раскраске нет клики на вершинах ни цвета , ни цвета , получили противоречи противоречие. Значит было выбрано неверно. Из этого следует . |
Свойства чисел Рамсея
Следующими свойствами удобно пользоваться при подсчете значений чисел Рамсея на практике.
Значения чисел Рамсея
Задача нахождения точных значений чисел Рамсея чрезвычайно трудна, их известно довольно мало. Далее приведена таблица Станислава Радзишевского [2], в которой присутствуют практически все известные числа Рамсея или же промежутки, в которых они находятся.
| Числа Рамсея | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Числа Рамсея для раскрасок в несколько цветов
Теперь обобщим числа Рамсея на произвольное количество цветов.
| Определение: |
| Число Рамсея — это наименьшее из всех таких чисел , что при любой раскраске рёбер полного графа на вершинах в цветов для некоторого обязательно найдётся клика на вершинах с рёбрами цвета . |
| Теорема (3,Теорема Рамсея для нескольких цветов): |
существует соответственное число Рамсея , при этом |
| Доказательство: |
| Возьмем граф из вершин и окрасим его рёбра в цветов. Пока что будем считать цвета и одним цветом. Тогда граф будет -цветным. Согласно определению числа Рамсея , такой граф либо содержит для некоторого цвета , такого что либо , окрашенный общим цветом и . В первом случае доказательство завершено. Во втором случае вернём прежние цвета и заметим, что, по определению числа Рамсея, полный — вершинный граф содержит либо цвета , либо цвета . Таким образом любое число Рамсея для раскраски в цветов ограничено некоторым числом Рамсея для меньшего количества цветов, следовательно, существует для любых , и теорема доказана. |
Числа Рамсея больших размерностей
| Определение: |
| Пусть , причём . Число Рамсея — наименьшее из всех таких чисел , что при любой раскраске -элементных подмножеств -элементного множества в цветов для некоторого обязательно найдётся такое множество , что и все -элементные подмножества множества имеют цвет . Число называют размерностью числа Рамсея . |
Нетрудно понять что числа Рамсея размерности — это определённые ранее числа Рамсея для клик.
При количестве цветов, равном , этот параметр в записи обычно опускают и пишут вместо .
| Определение: |
| Для каждою множества через мы будем обозначать множество всех -элементных подмножеств . |
| Теорема (4): |
Пусть — натуральные числа, причем , а . Тогда число Рамсея существует(то есть, конечно) |
| Доказательство: |
|
1)Мы будем доказывать теорему по индукции. Начнем со случая . Приступая к доказательству для числа мы будем считать доказанным утверждение теоремы для чисел Рамсея всех меньших размерностей и чисел Рамсея размерности с меньшей суммой . В качестве базы будем использовать случай чисел Рамсея размерности 2 разобранный выше. Итак, мы докажем, что
Рассмотрим -элементное множество и выделим в нём элемент . Пусть \{}. Пусть {1,2} — произвольная раскраска в два цвета. Рассмотрим раскраску {1,2}, определённую следующим образом: для каждого множества пусть {a}. Так как , либо существует -элементное подмножество , для которого на всех , либо существует -элементное подмножество , для которого на всех . Случаи аналогичны, рассмотрим первый случай и множество . По индукционному предположен из следует, что либо существует -элементное подмножество , для которого на всех , либо существует -элементное подмножество , для которого на всех . Во втором случае искомое подмножество найдено (это ), рассмотрим первый случай и множество {}. Пусть . Если , то и следовательно . Если же , то множество \{} и поэтому \{}. Учитывая, что , мы нашли искомое подмножество и в этом случае. 2)При будем вести индукцию по с доказанной выше базой . При мы докажем неравенство Для этого мы рассмотрим множество на вершинах и произвольную раскраску в цветов. Рассмотрим раскраску {}, в которой цвета раскраски склеены в цвет 0. Тогда существует либо таксе подмножество , что и на всех , либо существует такое -элементное подмножество , что на всех . Во втором случае — искомое подмножество, а в первом случае заметим, что на любом подмножестве из следует . Исходя из размера множества по индукционному предположению получаем, что найдется искомое подмножество множества для одного из цветов |
Числа Рамсея для произвольных графов
Еще один способ обобщения классической теории Рамсея — замена клик на произвольные графы-шаблоны.
| Определение: |
| Пусть — два данных графа. Число Рамсея — это наименьшее из всех таких чисел , что при любой раскраске рёбер полного графа на вершинах в два цвета обязательно найдется подграф, изоморфный с рёбрами цвета или подграф изоморфный с рёбрами цвета . |
Из результатов классической теории Рамсея становится понятно, что числа существуют.
| Лемма (1): |
Пусть , а граф таков, что и . Тогда граф содержит в качестве подграфа любое дерево на вершинах. |
| Доказательство: |
|
Зафиксируем и проведем индукцию по . База: для очевидно. Индукционный переход: Пусть верно для , докажем для . Рассмотрим произвольное дерево на вершинах, пусть дерево получено из удалением висячей вершины. Пусть — максимальное независимое множестве вершин графа . Тогда , следовательно и очевидно . По индукционному предположению, граф содержит в качестве подграфа дерево . Пусть — вершина этого дерева, присоединив к которой висячую вершину мы получим дерево . Заметим, что множество не является независимым ввиду максимальности . Следовательно, вершина смежна хотя бы с одной вершиной . Отметим, что и, присоединив вершину к вершине дерева , получим дерево в качестве подграфа графа . |
| Теорема (5): |
, где — дерево на вершинах. |
| Доказательство: |
|
Докажем, что . Для этого предъявим раскраску рёбер графа , в которой нет ни одного связного подграфа на вершинах с рёбрами цвета и нет клики на вершинах с рёбрами цвета . Разобьём вершины графа на клику по вершине и покрасим все рёбра этих клик в цвет . Тогда любой связный подграф с рёбрами цвета содержит не более вершины, в частности, нет подграфа с рёбрами цвета , изоморфного . Рёбра цвета (то есть, все оставшиеся рёбра) образуют -дольный граф, в котором, очевидно, нет клики на вершинах. Рассмотрим произвольную раскраску рёбер полного графа в два цвета. Предположим, что не существует клики на вершинах с рёбрами цвета . Тогда и . По лемме , граф содержит в качестве подграфа любое дерево на вершинах, в частности, дерево, изоморфное . |