Кросс-валидация

Кросс-валидация или скользящий контроль это процедура оценивания обобщающей способности алгоритмов. С помощью кросс-валидации эмулируется наличие тестовой выборки, которая не участвует в обучении, но для которой известны правильные ответы.

Определения

[math]T^l = {(x_i, y_i)}_{i=1}^{l}[/math] - обучающая выборка.

[math]Q[/math] - мера качества.

[math]\mu(T^l) = argmin_{a \in A}Q(a, T^l)[/math] - метод минимизации эмпирического риска.

Разновидности Кросс-валидации

Валидация на отложенных данных (Hold-Out Validation)

Обучающая выборка один раз случайным образом разбивается на две части [math] T^l = T^t \cup T^{l-t} [/math]

После чего решается задача оптимизации:

[math]HO(\mu, T^t, T^{l-t}) = Q(\mu(T^t), T^{l-t}) \to min [/math]

Метод Hold-out применяется в случаях больших датасетов, т.к. требует меньше вычислительных мощностей по сравнению с другими методами кросс-валидации. Недостатком метода является то, что оценка существенно зависит от разбиения, тогда как желательно, чтобы она характеризовала только алгоритм обучения.

Полная кросс-валидация (Complete cross-validation)

1. Выбирается значение [math]t[/math]
2. Выборка разбивается всеми возможными способами на две части [math] T^l = T^t \cup T^{l-t} [/math]

[math]CVV_t = \frac{1}{C_l^{l-t}} \displaystyle\sum_{T^l = T^t \cup T^{l-t}} Q(\mu(T^t), T^{l-t}) \to min [/math]

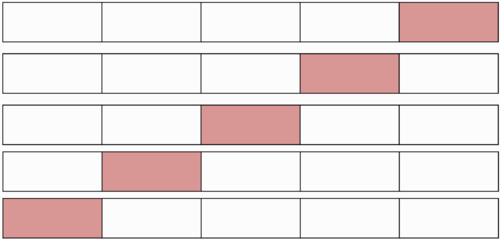
k-fold кросс-валидация

1. Обучающая выборка разбивается на [math] k [/math] непересекающихся одинаковых по объему частей
2. Производится [math] k [/math] итераций. На каждой итерации происходит следующее:
   1. Модель обучается на [math] k - 1 [/math] части обучающей выборки;
   2. Модель тестируется на части обучающей выборки, которая не участвовала в обучении;

[math]T^l = F_1 \cup \dots \cup F_k, |F_i| \approx \frac{l}{k} \\ CV_k = \frac{1}{k} \sum_{i=1}^{k} Q(\mu(T^l \setminus F_i),F_i) \to min [/math]

Каждая из [math]k[/math] частей единожды используется для тестирования. Как правило [math]k = 10[/math] (5 в случае малого размера выборки)

В результате можно посчитать различные метрики, показывающие, насколько модель удачная, например, среднюю ошибку на частях, которые не участвовали в обучающей выборке.

t×k-fold кросс-валидация

1. Процедура выполняется [math]t[/math] раз:
   1. Обучающая выборка случайным образом разбивается на [math]k[/math] непересекающихся одинаковых по объему частей
   2. Производится [math] k [/math] итераций. На каждой итерации происходит следующее:
      1. Модель обучается на [math] k - 1 [/math] части обучающей выборки;
      2. Модель тестируется на части обучающей выборки, которая не участвовала в обучении;

[math]T^l = F_{(1,1)} \cup \dots \cup F_{(k,1)} = \dots = F_{(1,t)} \cup \dots \cup F_{(k,t)}, |F_{(i,j)}| \approx \frac{l}{k} [/math]

[math] CV_{t \times k} = \frac{1}{tk} \sum_{j=1}^t \sum_{i=1}^{k} Q(\mu(T^l \setminus F_{(i,j)}),F_{(i,j)}) \to min [/math]

Кросс-валидация по отдельным объектам (leave-one-out)

Выборка разбивается на [math]l-1[/math] и 1 объект [math]l[/math] раз.

[math]LOO = \frac{1}{l} \sum_{i=1}^{l} Q(\mu(T^l \setminus p_i),p_i) \to min [/math], где [math]p_i = (x_i, y_i)[/math]

Случайные разбиения (Random subsampling)

Выборка разбивается в случайной пропорции. Процедура повторяется несколько раз.

Критерий целостности модели (Model consistency criterion)

Не переобученый алгоритм должен показывать одинаковую эффективность на каждой части

[math] D_1 = (\mu, T^{l-t}) = \frac{1}{l} \sum_{i=1}^l (\mu(T^t)(x_i)-\mu(T^{l-t})(x_i)) [/math]

Метод может быть обобщен как аналог [math] CV_{t \times 2} [/math].

См. также

• Общие понятия^{[на 17.01.19 не создан]}
• Модель алгоритма и ее выбор
• Мета-обучение^{[на 17.01.19 не создан]}

Примечания

1. Кросс-валидация
2. Автоматизированный выбор модели в библиотеке WEKA для Java
3. Автоматизированный выбор модели в библиотеке TPOT для Python
4. Автоматизированный выбор модели в библиотеке sklearn для Python

Источники информации

1. Скользящий контроль - статья на MachineLearning.ru
2. Model assessment and selection