Общие понятия
Понятие машинного обучения в искусственном интеллекте
| Определение: |
| Машинное обучение (англ. Machine learning) — процесс, который даёт возможность компьютерам обучаться выполнять что-то без явного написания кода. |
A.L. Samuel "Some Studies in Machine Learning Using the Game of Checkers" (IBM Journal. July 1959. P. 210–229)
| Определение: |
| Говорят, что компьютерная программа учится на опыте $E$ относительно некоторой задачи $T$ и некоторой меры производительности $P$, если ее производительность на $T$, измеренная $P$, улучшается с опытом $E$. |
T.M. Mitchell "Machine Learning" (McGraw-Hill, 1997)
Задача обучения
$X$ — множество объектов (англ. object set, or input set)
$Y$ — множество ответов (англ. label set, or output set)
$y ∶ X → Y$ — неизвестная зависимость (англ. unknown target function (dependency))
Компьютер всегда имеет дело с признаковым описанием объектов. Например: пациента можно описать признаками: имя, возраст, номер полиса, жалобы, давление, температура, результаты анализов.
$f_j∶ X → D_j,j = 1, ... , n$ — признаки (англ. features, or attributes).
Типы признаков:
- бинарный (binary): $D_j = \{0, 1\}$
- номинальный (categorical): $D_j$ конечно
- упорядоченный (ordinal): $D_j$ конечно и упорядоченно
- количественный (numerical): $D_j = \mathbb{R}$
т.е объект представляется как набор признаков $(f_1(x),... ,f_n(x))$. Данные обычно представляются в виде матрицы объектов-признаков
Дано
${x_1, . . . , x_l} ⊂ X$ — обучающая выбока (англ. training sample set)
$y_i = y(x_i), i = 1, . . . , l $ — известные ответы
Найти
Найти $ a ∶ X → Y $ — алгоритм, решающую функцию (англ. decision function), приближающую $y$ на всём множестве $X$.
Типы задач
Задачи классификации (англ. classification):
- $Y = \{−1, +1\}$ — классификация на 2 класса
- $Y = \{1, . . . , M\}$ — на $M$ непересекающихся классов
- $Y = \{0, 1\}^M$— на $M$ классов, которые могут пересекаться.
Примеры: распознавание текста по рукописному вводу, определение того, находится на фотографии человек или кот.
Задачи восстановления регрессии (англ. regression):
- $Y = \mathbb{R}$ или $Y = \mathbb{R}^m$
Примеры: предсказание стоимости акции через полгода, предсказание прибыли магазина в следующем месяце, предсказание качества вина на слепом тестировании.
Задачи ранжирования (англ. ranking):
- $Y$ — конечное упорядоченное множество
Пример: выдача поискового запроса.
Задачи уменьшения размерности
Научиться описывать данные не $N$ признаками, а меньшим числом (как правило, 2-3 для последующей визуализации). В качестве примера помимо необходимости для визуализации можно привести сжатие данных.
Задачи кластеризации
Разбиение данных на похожие категории.
Примеры: разбиение клиентов сотового оператора по платёжеспособности, разбиение космических объектов на похожие (галактики, планеты, звезды и так далее).
Задачи выявления аномалий
На основании признаков научиться различать отличать аномалии от «не-аномалий». Кажется, что от задачи классификации эта задача ничем не отличается. Но особенность выявления аномалий состоит в том, что примеров аномалий для тренировки модели у нас либо очень мало, либо нет совсем, поэтому мы не можем решать такую задачу как задачу классификации.
Пример: определение мошеннических транзакций по банковской карте.
Классификация задач машинного обучения
Обучение с учителем (англ. Supervised learning [1])
Тренировочные данные доступны все сразу и размечены (известны ответы для поставленной задачи).
Задачи которые могут решаться этим способом: классификация, регрессия, предсказание.
Обучение без учителя (англ. Unsupervised learning)
Изучает широкий класс задач обработки данных, в которых известны только описания множества объектов (обучающей выборки), и требуется обнаружить внутренние взаимосвязи, зависимости, закономерности, существующие между объектами.
т.е тренировочные данные доступны все сразу, но ответы для поставленной задачи неизвестны.
Задачи, которые могут решаться этим способом: кластеризация, нахождение ассоциативных правил, выдача рекомендаций (например реклама), уменьшение размености датасета.
Обучение с частичным привлечением учителя (англ. Semi-supervised learning)
Тренировочные данные доступны все сразу, но размечено мало, либо малоинформативная часть.
Примером частичного обучения может послужить сообучение: два или более обучаемых алгоритма используют один и тот же набор данных, но каждый при обучении использует различные — в идеале некоррелированные — наборы признаков объектов.
Обучение с подкреплением (англ. Reinforcement learning)
Частный случай обучения с учителем, сигналы подкрепления (правильности ответа) выдаются не учителем, а некоторой средой, с которой взаимодействует программа. Размеченность данных зависит от среды.
Активное обучение (англ. Active learning)
Отличается тем, что обучаемый имеет возможность самостоятельно назначать следующий прецедент, который станет известен.
Обучение в реальном времени (англ. Online learning)
Тренировочные данные поступают последовательно.
Структурное предсказание (англ. Structured prediction)
Выбор модели и валидация (англ. Model selection and validation)
Примеры задач
- Предсказание месторождений полезных ископаемых
Признаками являются данные геологической разведки. Наличие или отсутствие тех или иных пород на территории района кодируется бинарными признаками. Физико-химические свойства этих пород могут описываться как количественными, так и качественными признаками. Обучающая выборка составляется из прецедентов двух классов: районов известных месторождений и похожих районов, в которых интересующее ископаемое обнаружено не было. При поиске редких полезных ископаемых количество объектов может оказаться намного меньше, чем количество признаков. В этой ситуации плохо работают классические статистические методы. Задача решается путём поиска закономерностей в имеющемся массиве данных. В процессе решения выделяются короткие наборы признаков, обладающие наибольшей информативностью — способностью наилучшим образом разделять классы. По аналогии с медицинской задачей, можно сказать, что отыскиваются «синдромы» месторождений. Это важный побочный результат исследования, представляющий значительный интерес для геофизиков и геологов.
- Оценивание кредитоспособности заёмщиков
Эта задача решается банками при выдаче кредитов. Потребность в автоматизации процедуры выдачи кредитов впервые возникла в период бума кредитных карт 60-70-х годов в США и других развитых странах. Объектами в данном случае являются физические или юридические лица, претендующие на получение кредита. В случае физических лиц признаковое описание состоит из анкеты, которую заполняет сам заёмщик, и, возможно, дополнительной информации, которую банк собирает о нём из собственных источников. Примеры бинарных признаков: пол, наличие телефона. Номинальные признаки — место проживания, профессия, работодатель. Порядковые признаки — образование, занимаемая должность. Количественные признаки — сумма кредита, возраст, стаж работы, доход семьи, размер задолженностей в других банках. Обучающая выборка составляется из заёмщиков с известной кредитной историей. В простейшем случае принятие решений сводится к классификации заёмщиков на два класса: «хороших» и «плохих». Кредиты выдаются только заёмщикам первого класса. В более сложном случае оценивается суммарное число баллов (score) заёмщика, набранных по совокупности информативных признаков. Чем выше оценка, тем более надёжным считается заёмщик. Отсюда и название — кредитный скоринг. На стадии обучения производится синтез и отбор информативных признаков и определяется, сколько баллов назначать за каждый признак, чтобы риск принимаемых решений был минимален. Следующая задача — решить, на каких условиях выдавать кредит: определить процентную ставку, срок погашения, и прочие параметры кредитного договора. Эта задача также может быть решения методами обучения по прецедентам.
- Прогнозирование потребительского спроса
Решается современными супермаркетами и торговыми розничными сетями. Для эффективного управления торговой сетью необходимо прогнозировать объёмы продаж для каждого товара на заданное число дней вперёд. На основе этих прогнозов осуществляется планирование закупок, управление ассортиментом, формирование ценовой политики, планирование промоакций (рекламных кампаний). Специфика задачи в том, что количество товаров может исчисляться десятками или даже сотнями тысяч. Прогнозирование и принятие решений по каждому товару «вручную» просто немыслимо. Исходными данными для прогнозирования являются временные ряды цен и объёмов продаж по товарам и по отдельным магазинам. Современные технологии позволяют снимать эти данные непосредственно с кассовых аппаратов. Для увеличения точности прогнозов необходимо также учитывать различные внешние факторы, влияющие на потребительский спрос: уровень инфляции, погодные условия, рекламные кампании, социально-демографические условия, активность конкурентов. В зависимости от целей анализа в роли объектов выступают либо товары, либо магазины, либо пары «магазин, товар». Ещё одна особенность задачи — несимметричность функции потерь. Если прогноз делается с целью планирования закупок, то потери от заниженного прогноза существенно выше потерь от завышенного.
- Принятие инвестиционных решений на финансовом рынке
В этой задаче умение хорошо прогнозировать самым непосредственным образом превращается в прибыль. Если инвестор предполагает, что цена акции вырастет, он покупает акции, надеясь продать их позже по более высокой цене. И, наоборот, прогнозируя падение цен, инвестор продаёт акции, чтобы впоследствии выкупить их обратно по более низкой цене. Задача инвестора-спекулянта в том, чтобы правильно предугадать направление будущего изменения цены — роста или падения. Большой популярностью пользуются автоматические торговые стратегии -алгоритмы, принимающие торговые решения без участия человека. Разработка такого алгоритма — тоже задача обучения с учителем. В роли объектов выступают ситуации, фактически, моменты времени. Описание объекта — это вся предыстория изменения цен и объёмов торгов, зафиксированная к данному моменту. В простейшем случае объекты необходимо классифицировать на три класса, соответствующих возможным решениям: купить, продать или выжидать. Обучающей выборкой для настройки торговых стратегий служат исторические данные о движении цен и объёмов за некоторый промежуток времени. Критерий качества в данной задаче существенно отличается от стандартного функционала средней ошибки, поскольку инвестора интересует не точность прогнозирования, а максимизация итоговой прибыли. Современный биржевой технический анализ насчитывает сотни параметрических торговых стратегий, параметры которых принято настраивать по критерию максимума прибыли на выбранном интервале истории.
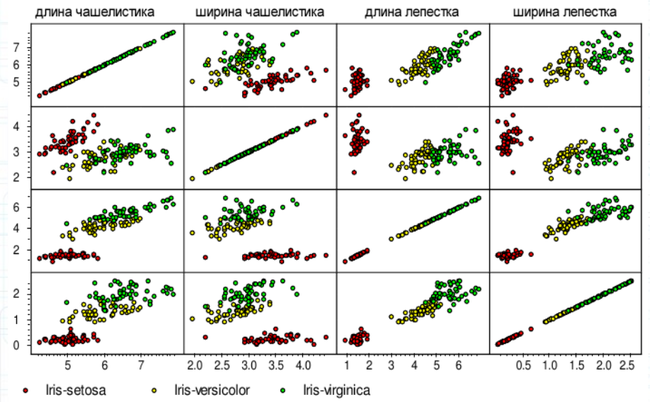
- Задача классификации видов ириса (Фишер 1936) [2]
См. также
Примечания
Источники информации
- Машинное обучение — Wiki
- Курс лекций по машинному обучению — Воронцов К.В.
- Статья "Машинное обучение для чайников"