Вариации регрессии
Регрессия (англ. Regression) — метод моделирования зависимости между зависимой переменной и одной или несколькими независимыми переменными . В случае нескольких независимых переменных регрессия называется множественной (англ. multivariate regression). Цель регрессионного анализа состоит в том, чтобы оценить значение непрерывной выходной переменной по значениям входных переменных.
Линейная регрессия
Линейная регрессия (англ. linear regression) — разновидность регрессии для моделирования линейной зависимости между зависимой и независимой переменными.
Логистическая регрессия
Логистическая регрессия (англ. logistic regression) — разновидность регрессии для прогнозирования вероятности некоторого события по значениям независимых переменных. Зависимая переменная в этом случае принимает значения или (рассматриваемое событие не произошло или произошло соответственно).
Гребневая регрессия (ридж-регрессия)
Гребневая регрессия или ридж-регрессия (англ. ridge regression) — один из методов понижения размерности. Применяется для борьбы с избыточностью данных, когда независимые переменные коррелируют друг с другом, вследствие чего проявляется неустойчивость оценок коэффициентов многомерной линейной регрессии.
Мотивация
| Определение: |
| Мультиколлинеарность (англ. multicollinearity) — наличие линейной зависимости между независимыми переменными регрессионной модели. Различают полную коллинеарность и частичную или просто мультиколлинеарность — наличие сильной корреляции между независимыми переменными. |
Рассмотрим пример линейной модели: . Пусть имеет место зависимость . Добавим к первому коэффициенту произвольное число , а из двух других коэффициентов это же число вычтем. Получаем (без случайной ошибки):
Несмотря на относительно произвольное изменение коэффициентов модели мы получили исходную модель, то есть такая модель неидентифицируема.
На практике чаще встречается проблема сильной корреляции между независимыми переменными. В этом случае оценки параметров модели получить можно, но они будут неустойчивыми.
Описание
Напомним задачу многомерной линейной регрессии:
Рассматривается линейная зависимость .
Находим вектор , при котором достигается минимум среднего квадрата ошибки:
Методом наименьших квадратов находим решение:
В условиях мультиколлинеарности матрица становится плохо обусловленной.
Для решения этой проблемы наложим ограничение на величину коэффициентов : .
Функционал с учетом ограничения принимает вид:
- ,
где — неотрицательный параметр.
Решением в этом случае будет
Это изменение увеличивает собственные значения матрицы , но не изменяет ее собственные вектора. В результате имеем хорошо обусловленную матрицу.
Диагональная матрица называется гребнем.
Пример кода для Scikit-learn
# импорт библиотек from sklearn.datasets import make_regression from sklearn.linear_model import Ridge from sklearn.model_selection import train_test_split # генерируем данные для X и y X, y = make_regression(n_samples=10000, noise=100, random_state=0) # разделение данных на train и test train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.3, random_state=3) ridge_regression = Ridge(alpha=0.1) # alpha — величина регуляризации # обучение ridge_regression.fit(train_X, train_y) # предсказание результата print(ridge_regression.predict(test_X)) # вывод точности предсказания print(ridge_regression.score(test_X, test_y))
Точность предсказания для данного датасета и параметров:
>>> 0.8171822749108134
Лассо-регрессия
Метод регрессии лассо (англ. LASSO, Least Absolute Shrinkage and Selection Operator) похож на гребневую регрессию, но он использует другое ограничение на коэффициенты :
Функционал принимает следующий вид:
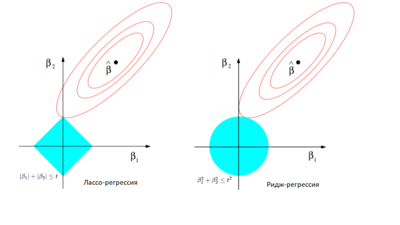
Основное различие лассо- и ридж-регрессии заключается в том, что первая может приводить к обращению некоторых независимых переменных в ноль, тогда как вторая уменьшает их до значений, близких к нулю. Рассмотрим для простоты двумерное пространство независимых переменных. В случае лассо-регрессии органичение на коэффициенты представляет собой ромб (), в случае ридж-регрессии — круг (). Необходимо минимизировать функцию ошибки, но при этом соблюсти ограничения на коэффициенты. С геометрической точки зрения задача состоит в том, чтобы найти точку касания линии, отражающей функцию ошибки с фигурой, отражающей ограничения на . Из рисунка 1 интуитивно понятно, что в случае лассо-регрессии эта точка с большой вероятностью будет находиться на углах ромба, то есть лежать на оси, тогда как в случае ридж-регрессии такое происходит очень редко. Если точка пересечения лежит на оси, один из коэффициентов будет равен нулю, а значит, значение соответствующей независимой переменной не будет учитываться.
Пример кода для Scikit-learn
# импорт библиотек from sklearn.datasets import make_regression from sklearn.linear_model import Lasso from sklearn.model_selection import train_test_split # генерируем данные для X и y X, y = make_regression(n_samples=10000, noise=100, random_state=0) # разделение данных на train и test train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.3, random_state=3) lasso_regression = Lasso(alpha=0.1) # alpha — величина регуляризации # обучение lasso_regression.fit(train_X, train_y) # предсказание результата print(lasso_regression.predict(test_X)) # вывод точности предсказания print(lasso_regression.score(test_X, test_y))
Точность предсказания для данного датасета и параметров:
>>> 0.8173906804156383
Байесовская регрессия
Описанные выше методы никак не учитывали наличие в данных шума, тогда как в реальных данных он скорее всего будет присутствовать. Предположим, что в данных все же есть некоторый шум, и что он распределен нормально. Тогда задачу линейной регрессии можно записать в следующем виде:
- , где .
Решением этой задачи мы и будем заниматься в этом разделе.
Байесовская линейная регрессия (англ. Bayesian linear regression) — подход в линейной регрессии, в котором предполагается что шум распределен нормально.
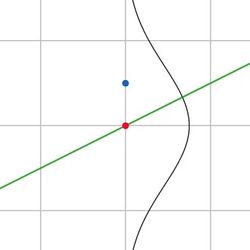
На рисунке 2 синяя точка показывает значения из датасета, красная — значение, предсказанное регрессией. Поскольку центр гауссианы находится в красной точке, маленькие отклонения синей точки от красной более вероятны, а большие менее вероятны.
Для решения поставленной задачи регрессии воспользуемся методом максимального правдоподобия.
Запишем правдоподобие:
- ,
где — плотность распределения значения из датасета, которая, как мы ранее предположили, соответствует нормальному распределению с центром в точке (значение для , предсказанное алгоритмом).
Будем также предполагать, что данные независимы:
Поскольку нас интересует только максимум, положим :
Прологарифмируем это выражение:
Таким образом, оказывается, что метод максимального правдоподобия с учетом шума в данных сводится к оценке по методу наименьших квадратов, которую мы уже видели в обынчой линейной регрессии.
Пример кода для Scikit-learn
# импорт библиотек from sklearn.datasets import make_regression from sklearn.linear_model import BayesianRidge from sklearn.model_selection import train_test_split # генерируем данные для X и y X, y = make_regression(n_samples=10000, noise=100, random_state=0) # разделение данных на train и test train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.3, random_state=3) bayesian_regression = BayesianRidge() # обучение bayesian_regression.fit(train_X, train_y) # предсказание результата print(bayesian_regression.predict(test_X)) # вывод точности предсказания print(bayesian_regression.score(test_X, test_y))
Точность предсказания для данного датасета и параметров:
>>> 0.8170548749907206
Логическая регрессия
Логическая регрессия (англ. logic regression) — обобщенный метод регрессии, применяемый в основном в случае, когда независимые переменные имеют двоичную природу (при этом зависимая переменная не обязательно двоичная). Задачей логической регрессии является определение независимых переменных, которые могут быть выражены как результат вычисления булевой функции от других независимых переменных.
Обычно в методах регрессии не учитывается связь между переменными. Предполагается, что влияние каждой переменной на результат не зависит от значений других переменных. Однако это предположение зачастую неверно.
Пусть — двоичные независимые переменные, и пусть — зависимая переменная. Будем пытаться натренировать модели регрессии вида , где — булева функция от переменных (например ). Для каждого типа модели необходимо определить функцию, которая отражает качество рассматриваемой модели. Например, для линейной регрессии такой функцией может быть остаточная сумма квадратов. Целью метода логической регрессии является минимизация выбранной функции качества посредством настройки параметров одновременно с булевыми выражениями .
Может показаться не совсем понятным, как же применить регрессию к булевым выражениям. Рассмотрим в общих чертах алгоритм логической регрессии. Логическая регрессия, как и другие методы регрессии, перебирает различные выражения в попытках минимизировать функцию потерь. Для переменных можно составить различных выражений. Нужно найти более эффективный метод для поиска наилучшего выражения, чем простой перебор всех вариантов.
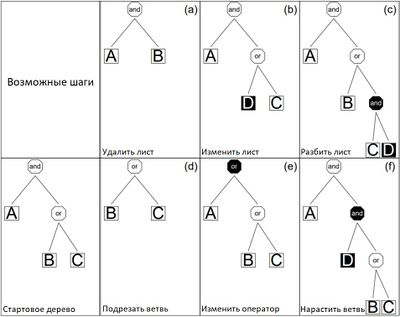
Любое логическое выражение можно представить в виде дерева, где в узлах расположены операции, а листья представляют собой переменные. Будем называть такие деревья логическими деревьями (англ. logic trees). Будем называть соседями (англ. neighbours) логического дерева такие деревья, которые могут быть получены из него за один шаг. Допустимые шаги проиллюстрированы на рисунке 3.
Рассмотрим самый простой алгоритм поиска наилучшего дерева — жадный поиск (англ. greedy search).
- В качестве стартового дерева выберем одну переменную, которая дает минимальное значение функции потерь среди всех остальных переменных.
- Перебираем соседей текущего дерева и выбираем такое, что оно уменьшает значение функции потерь по сравнению с текущим, а также дает наименьший результат среди остальных соседей.
- Если такого дерева не существует, алгоритм завершается. Если оно все же есть, выбираем его в качестве текущего и повторяем второй шаг.
Этот алгоритм склонен к переобучению, а также в некоторых ситуациях может остановиться преждевременно, так и не дойдя до наилучшего дерева. Существует также алгоритм под названием имитация отжига (англ. simulated annealing) который показывает лучшие результаты, чем описанный жадный поиск.
См. также
Источники информации
- 10 типов регрессии — какой выбрать?
- machinelearning.ru — Линейная регрессия (пример)
- machinelearning.ru — Ридж-регрессия
- Лекции по алгоритмам восстановления регрессии К. В. Воронцов
- Ridge and Lasso Regression: A Complete Guide with Python Scikit-Learn
- Habr — Базовые принципы машинного обучения на примере линейной регрессии
- Documents on Logic Regression