Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.
Чтобы понять математическое предназначение метода, требуется осознать взаимоотношения между действительными выходными значениями сети и требуемыми выходными значениями для конкретного примера из обучения. Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации,
[заметка 1] которая является взвешенной суммой входных данных.
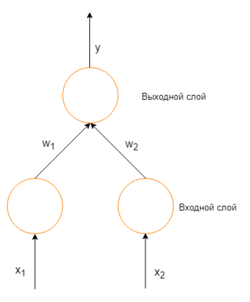
Простая нейронная сеть с двумя входными вершинами и одной выходной
Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек [math](x_1, x_2, t)[/math] где [math]x_1[/math] и [math]x_2[/math] — это входные данные сети и [math]t[/math] — правильный ответ. Начальная сеть, приняв на вход [math]x_1[/math] и [math]x_2[/math], вычислит ответ [math]y[/math], который вероятно отличается от [math]t[/math]. Общепринятый метод вычисления несоответствия между ожидаемым [math]t[/math] и получившимся [math]y[/math] ответом — квадратичная функция потерь:
- [math]E=(t-y)^2, [/math] где [math]E[/math] ошибка.
В качестве примера, рассмотрим сеть с одним тренировочным объектом:
[math](1, 1, 0)[/math], таким образом, значения
[math]x_1[/math] и
[math]x_2[/math] равны 1, а
[math]t[/math] равно 0. Теперь, если действительный ответ
[math]y[/math] изобразить на графике на горизонтальной оси, а ошибку
[math]E[/math] на вертикальной, результатом будет парабола. Минимум параболы соответствует ответу
[math]y[/math], который минимизирует ошибку
[math]E[/math]. Для одиночного тренировочного объекта, минимум также касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ
[math]y[/math] который точно соответствует ожидаемому ответу
[math]t[/math]. Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.
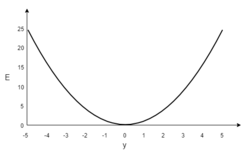
График ошибки для нейрона с линейной функцией активации и одним тренировочным объектом
В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:
- [math]y=x_1w_1 + x_2w_2,[/math]
где [math]w_1[/math] и [math]w_2[/math] — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого "крутого" направления для спуска.
Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один,[заметка 2] тогда квадратичная функция ошибки:
- [math]E = \tfrac 1 2 (t - y)^2,[/math] где [math]E[/math] — квадратичная ошибка, [math]t[/math] — требуемый ответ для обучающего образца, [math]y[/math] — действительный ответ сети.
Множитель [math]\textstyle\frac{1}{2}[/math] добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. На результат это не повлияет, потому что позже выражение будет умножено на произвольную величину скорости обучения (англ. learning rate).
Для каждого нейрона [math]j[/math], его выходное значение [math]o_j[/math] определено как
- [math]o_j = \varphi(\text{net}_j) = \varphi\left(\sum_{k=1}^n w_{kj}o_k\right).[/math]
Входные значения [math]\text{net}_j[/math] нейрона — это взвешенная сумма выходных значений [math]o_k[/math] предыдущих нейронов. Если нейрон в первом слове после входного слоя, то [math]o_k[/math] входного слоя — это просто входные значения [math]x_k[/math] сети. Количество входных значений нейрона [math]n[/math]. Переменная [math]w_{kj}[/math] обозначает вес на ребре между нейроном [math]k[/math] предыдущего слоя и нейроном [math]j[/math] текущего слоя.
Функция активации [math]\varphi[/math] нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:
- [math] \varphi(z) = \frac 1 {1+e^{-z}}[/math]
у нее удобная производная:
- [math] \frac {d \varphi(z)}{d z} = \varphi(z)(1-\varphi(z)) [/math]
Находим производную ошибки
Вычисление частной производной ошибки по весам [math]w_{ij}[/math] выполняется с помощью цепного правила:
- [math]\frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial o_j} \frac{\partial o_j}{\partial\text{net}_j} \frac{\partial \text{net}_j}{\partial w_{ij}}[/math]
Только одно слагаемое в [math]\text{net}_j[/math] зависит от [math]w_{ij}[/math], так что
- [math]\frac{\partial \text{net}_j}{\partial w_{ij}} = \frac{\partial}{\partial w_{ij}} \left(\sum_{k=1}^n w_{kj} o_k\right) = \frac{\partial}{\partial w_{ij}} w_{ij} o_i= o_i.[/math]
Если нейрон в первом слое после входного, то [math]o_i[/math] — это просто [math]x_i[/math].
Производная выходного значения нейрона [math]j[/math] по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):
- [math]\frac{\partial o_j}{\partial\text{net}_j} = \frac {\partial}{\partial \text{net}_j} \varphi(\text{net}_j) = \varphi(\text{net}_j)(1-\varphi(\text{net}_j))[/math]
По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)
Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае [math]o_j = y[/math] и
- [math]\frac{\partial E}{\partial o_j} = \frac{\partial E}{\partial y} = \frac{\partial}{\partial y} \frac{1}{2}(t - y)^2 = y - t [/math]
Тем не менее, если [math]j[/math] произвольный внутренний слой сети, нахождение производной [math]E[/math] по [math]o_j[/math] менее очевидно.
Если рассмотреть [math]E[/math] как функцию, берущую на вход все нейроны [math]L = {u, v, \dots, w}[/math] получающие на вход значение нейрона [math]j[/math],
- [math]\frac{\partial E(o_j)}{\partial o_j} = \frac{\partial E(\mathrm{net}_u, \text{net}_v, \dots, \mathrm{net}_w)}{\partial o_j}[/math]
и взять полную производную по [math]o_j[/math], то получим рекурсивное выражение для производной:
- [math]\frac{\partial E}{\partial o_j} = \sum_{\ell \in L} \left(\frac{\partial E}{\partial \text{net}_\ell}\frac{\partial \text{net}_\ell}{\partial o_j}\right) = \sum_{\ell \in L} \left(\frac{\partial E}{\partial o_\ell}\frac{\partial o_\ell}{\partial \text{net}_\ell}w_{j\ell}\right)[/math]
Следовательно, производная по [math]o_j[/math] может быть вычислена если все все производные по выходным значениям [math]o_\ell[/math] следующего слоя известны.
Если собрать все месте:
- [math] \frac{\partial E}{\partial w_{ij}} = \delta_j o_i [/math]
и
- [math]\delta_j = \frac{\partial E}{\partial o_j} \frac{\partial o_j}{\partial\text{net}_j} = \begin{cases}
(o_j-t_j)o_j(1-o_{j}) & \text{если } j \text{ является нейроном выходного слоя,}\\
(\sum_{\ell\in L} w_{j\ell} \delta_\ell)o_j(1-o_j) & \text{если } j \text{ является нейроном внутреннего слоя.}
\end{cases}[/math]
Чтобы обновить вес [math]w_{ij}[/math] используя градиентный спуск, нужно выбрать скорость обучения, [math]\eta \gt 0[/math]. Изменение в весах должно отражать влияние [math]E[/math] на увеличение или уменьшение в [math]w_{ij}[/math]. Если [math]\frac{\partial E}{\partial w_{ij}} \gt 0[/math], увеличение [math]w_{ij}[/math] увеличивает [math]E[/math]; наоборот, если [math]\frac{\partial E}{\partial w_{ij}} \lt 0[/math], увеличение [math]w_{ij}[/math] уменьшает [math]E[/math]. Новый [math]\Delta w_{ij}[/math] добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на [math]-1[/math] гарантирует что [math]w_{ij}[/math] изменения будут всегда уменьшать [math]E[/math]. Другими словами, в следующем уравнении, [math]- \eta \frac{\partial E}{\partial w_{ij}}[/math] всегда изменяет [math]w_{ij}[/math] в такую сторону, что [math]E[/math] уменьшается:
- [math] \Delta w_{ij} = - \eta \frac{\partial E}{\partial w_{ij}} = - \eta \delta_j o_i[/math]
Недостатки алгоритма
Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
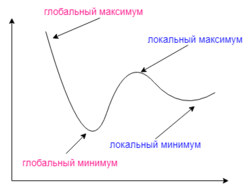
Градиентный спуск может найти локальный минимум вместо глобального
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.
Локальные минимумы
Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.
Алгоритм
Алгоритм:
BackPropagation [math](\eta, \alpha, \{x_i^d, t^d\}_{i=1,d=1}^{n,m}, \textrm{steps})[/math]
- Инициализировать [math]\{w_{ij}\}_{i,j} [/math] маленькими случайными значениями, [math]\{\Delta w_{ij}\}_{i,j} = 0[/math]
- Повторить [math]steps[/math] раз:
- .Для всех d от 1 до m:
- Подать [math]\{x_i^d\}[/math] на вход сети и подсчитать выходы [math]o_i[/math] каждого узла.
- Для всех [math]k \in Outputs[/math]
- [math]\delta _k = o_k(1 - o_k)(t_k - o_k)[/math].
- Для каждого уровня l, начиная с предпоследнего:
- Для каждого узла j уровня l вычислить
- [math]\delta _j = o_j(1 - o_j)\sum_{k \in Children(j)} \delta _k w_{j,k}[/math].
- Для каждого ребра сети {i, j}
- [math]\Delta w_{i,j}(n) = \alpha \Delta w_{i,j}(n-1) + ( 1 - \alpha ) \eta \delta _j o_{i}[/math].
- [math]w_{i,j}(n) = w_{i,j}(n-1) + \Delta w_{i,j}(n)[/math].
- Выдать значения [math]w_{ij}[/math].
где [math]\alpha[/math] — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции
Заметки
- ↑ Обычно, многослойные нейронные сети используют нелинейные функции активации, линейные функции используются для упрощения понимания.
- ↑ Их может быть несколько, тогда ошибка — это квадратичная норма вектора разницы.
См. такжеИсточники информации

