Симуляция одним распределением другого
Распределение
Распределение — одно из основных понятий теории вероятностей и математической статистики. Распределение вероятностей какой-либо случайной величины задается в простейшем случае указанием возможных значений этой величины и соответствующих им вероятностей, в более сложных — т. н. функцией распределения или плотностью вероятности.
Примеры распределений
- Биномиальное распределение
- Нормальное распределение
- Равномерное распределение
Симуляция распределений
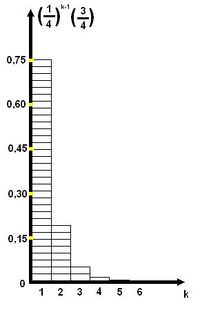
Рассмотрим следующий случай. Допустим, у нас есть честная монета. А нам надо получить распределения с вероятностями . Проведем селдующий эксперимент. Подкинем монету дважды. И если выпадет два раза орел - эксперимент не удался, повторим его. Предположим, что у нас есть последовательность экспериментов. Вероятность успеха . Вероятность неудачи Сколько экспериментов будет проведено до того, как будет достигнут успех? Пусть случайная величина равна количествуэкспериментов, необходимых для достижения успеха. Тогда принимает значения и для
поскольку перед наступлением успешного эксперимента было проведено неуспешных. Распределение вероятности, удовлетворяющее этому уравнению называется геометрическим распределением. Так как можно посчитать математическое ожидание геометрического распределения.
Дисперсия вычисляется аналогично.
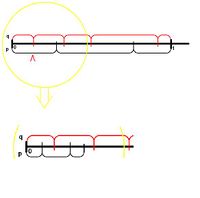
Рассмотрим теперь общий случай. Допустим у нас есть распределение Нам нужно получить распределение :
- и Проводим эксперимент, если попадаем в область пересекающуюся с и то увеличиваем ее и повторяем эксперимент. Вероятность неудачи на шаге — Математическое ожидание количества экспериментов —
- Повторим эксперимент раз. Отрезок разбился на отрезков. Стык будет не более, чем в половине отрезков. Математическое ожидание количества экспериментов
- Берем p_i и пусть оно максимальной длины. Проводим t экспериментов. {p_i}^t < \frac{1}{2n}, </tex> все остальные еще меньше. Суммарная длина отрезков не больше Нужно
Вывод: из любого исходного распределения можно получить любое.
См. также
Литература
- Боровков А.А. Математическая статистика: оценка параметров, проверка гипотез. - М., Физматлит, 1984.
- Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн - Алгоритмы. Построение и анализ 1244c.