Регуляризация

Определение:

Регуляризация (англ. regularization) в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить неккоректно поставленную задачу или предотвратить переобучение. Чаще всего эта информация имеет вид штрафа за сложность модели.

Мотивация

Как говорилось ранее, регуляризация полезна для борьбы с переобучением. Если вы выбрали сложную модель, и при этом у вас недостаточно данных, то легко можно получить итоговую модель, которая хорошо описывает обучающую выборку, но не обобщается на тестовую.

На примере линейной регрессии

В качестве наглядного примера можно рассмотреть линейные регрессионные модели. Восстановить зависимость для нескольких точек можно пытаться полиномами разной степени M.

Рис. 1. Норма. M = 2

Рис. 2. Переобучение. M = 4

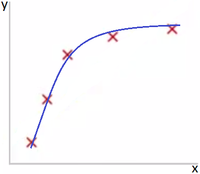
На Рис 1. представлена зависимость, которая хорошо подходит для описания данных, а на Рис. 2 — модель слишком сильно заточилась под обучающую выборку.

Одним из способов бороться с этим эффектом — использовать регуляризацию, т. е. добавлять некоторый штраф за большие значения коэффициентов у линейной модели. Тем самым мы запретим слишком "резкие" изгибы и ограничим возможность подстраивания модели под данные.

На примере логистической регрессии

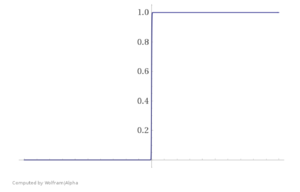
Необходимость регуляризации можно увидеть и на другом примере. Представьте, что ваша обучающая выборка была линейно разделима. В таком случае в процессе оптимизации значения весов уйдут в бесконечность и вместо сигмойды получится "ступенька", как представлено на Рис. 3.

Рис 3. Сигмойда — "ступенька"

Это плохо, ибо мы переобучились на нашу обучающую выборку. Как и в предыдущем примере, побороться с этим можно путем добавлением регуляризации, не дающей весам принимать слишком большие значения.

Основные виды регуляризации

Переобучение в большинстве случаев проявляется в том, что итоговые модели имеют слишком большие значения параметров. Соответственно, необходимо добавить в целевую функцию штраф за это. Наиболее часто используемые виды регуляризации — [math]L_{1}[/math] и [math]L_{2}[/math], а также их линейная комбинация — эластичная сеть.

В представленных ниже формулах для эмпирического риска [math]Q[/math]: [math]\mathcal{L}[/math] является функцией потерь, а [math]\beta[/math] — вектором параметров элемента [math]g(x, \beta)[/math] модели алгоритмов.

[math]L_{2}[/math]-регуляризация

Определение:

[math]L_{2}[/math]-регуляризация, или регуляризация Тихонова (англ. ridge regularization или Tikhonov regularization): [math]Q(\beta, X^l)=\sum\limits_{i=1}^l\mathcal{L}(y_{i}, g(x_{i}, \beta))+\lambda \sum\limits_{j=1}^n{\beta_{j}}^{2}[/math].

Минимизация регуляризованного cоответствующим образом эмпирического риска приводит в данном случае к выбору такого вектора параметров [math]\beta[/math], которое не слишком сильно отклоняется от нуля. В линейных классификаторах это позволяет избежать проблем мультиколлинеарности и переобучения.

[math]L_{1}[/math]-регуляризация

Определение:

[math]L_{1}[/math]-регуляризация(англ. lasso regularization), или регуляризация через манхэттенское расстояние: [math]Q(\beta, X^l)=\sum\limits_{i=1}^l\mathcal{L}(y_{i}, g(x_{i}, \beta))+\lambda \sum\limits_{j=1}^n{|\beta_{j}|}[/math].

Данный вид регуляризации также позволяет ограничить значения вектора [math]\beta[/math]. Однако, он также обладает интересным и полезным на практике свойством — обнуляет значения некоторых параметров, что в случае с линейными моделями приводит к отбору признаков.

Запишем задачу настройки вектора параметров [math]\beta[/math]:

[math]Q(\beta) = \sum\limits_{i=1}^l\mathcal{L}_{i}(\beta) + \lambda \sum\limits_{j=1}^n{|\beta_{j}|}[/math],

где [math]\mathcal{L}_{i}(\beta) = \mathcal{L}(y_{i}, g(x_{i}, \beta))[/math] — некоторая ограниченная гладкая функция потерь. Сделаем замену переменных, чтобы функционал стал гладким. Каждой переменной [math]\beta_{j}[/math] поставим в соответствие две новые неотрицательные переменные:

[math]\begin{cases} u_{j}=\frac{1}{2}(|\beta_{j}| + \beta_{j}) \\ v_{j}=\frac{1}{2}(|\beta_{j}| - \beta_{j}) \end{cases} [/math]

Тогда:

[math]\begin{cases} \beta_{j} = u_{j} - v_{j} \\ |\beta_{j}| = u_{j} + v_{j} \end{cases}[/math]

В новых переменных функционал становится гладким, но добавляется ограничения-неравенства:

[math]\begin{cases} Q(u, v) = \sum\limits_{i=1}^l\mathcal{L}_{i}(u - v) + \lambda \sum\limits_{j=1}^n(u_{j} + v_{j}) \rightarrow min_{u,v} \\ u_{j} \geq 0, v_{j} \geq 0, \: j=1,...,n\end{cases} [/math]

Для любого [math]j[/math] хотя бы одно из ограничений [math]u_{j} \geq 􏰧0[/math] и [math]v_{j} 􏰧\geq 0[/math] обращается в равенство, иначе второе слагаемое в [math]Q(u, v)[/math] можно было бы уменьшить, не изменив первое. Если гиперпараметр [math]\lambda[/math] устремить к [math]\infty[/math], в какой-то момент [math]2n[/math] ограничений обратятся в равенство. Постепенное увеличение гиперпараметра [math]\lambda[/math] приводит к увеличению числа таких [math]j[/math], для которых [math]u_{j} = v_{j} = 0[/math], откуда следует, что [math]w_{j} = 0[/math]. Как говорилось ранее, в линейных моделях это означает, что значения [math]j[/math]-го признака игнорируются, и его можно исключить из модели.

Эластичная сеть

Определение:

Эластичная сеть (англ. elastic net regularization): [math]Q(\beta, X^l)=\sum\limits_{I=1}^l\mathcal{L}(y_{i}, g(x_{i}, \beta))+\lambda_{1} \sum\limits_{j=1}^n{|\beta_{j}|}+\lambda_{2} \sum\limits_{j}{\beta_{j}}^{2}[/math].

Приведенная регуляризация использует как [math]L_{1}[/math], так и [math]L_{2}[/math] регуляризации, учитывая эффективность обоих методов. Ее полезной особенностью является то, что она создает условия для группового эффекта при высокой корреляции переменных, а не обнуляет некоторые из них, как в случае с [math]L_{1}[/math]-регуляризацией.

Вероятностная интерпретация регуляризации

Эквивалентная вероятностная задача

Перед нами стоит задача — минимизировать эмпирический риск:

[math]Q(\beta, X^l)=\sum\limits _{i=1}^l\mathcal{L}(y_{i}, g(x_{i}, \beta)) \rightarrow min_{\beta}[/math]

Вероятностная модель данных дает возможность по-другому взглянуть на задачу. Пусть [math]X \times Y[/math] — является вероятностным пространством. Тогда вместо [math]g(x_{i}, \beta)[/math] задана совместная плотность распределение объектов и классов [math]p(x, y|\beta)[/math].

Для настройки вектора параметров \beta воспользуемся принципом максимума правдоподобия:

[math]p(X^l|\beta)=\prod\limits_{i=1}^lp(x_{i},y_{i}|\beta) \rightarrow max_{\beta}[/math]

Удобнее рассматривать логарифм правдоподобия:

[math]L(\beta, X^l)=\ln p(X^l|\beta)=\sum\limits_{i=1}^l \ln p(x_{i}, y_{i}|\beta) \rightarrow max_{\beta}[/math]

Можно заключить, что задачи в исходном и вероятностном представлении эквивалентны, если положить:

[math]-\ln p(x_{i}, y_{i}|\beta)=\mathcal{L}(y_{i}, g(x_{i}, \beta))[/math]

Принцип максимума совместного правдоподобия данных и модели

Допустим, что наряду с параметрической моделью плотности распределения [math]p(x, y|\beta)[/math] имеется еще и априорное распределение в пространстве параметров модели [math]p(\beta)[/math]. Чтобы ослабить априорные ограничения, вместо фиксированной функции [math]p(w)[/math] вводится параметрическое семейство априорных распределений [math]p(\beta; \gamma)[/math], где [math]\gamma[/math] — гиперпараметр.

Принцип максимума правдоподобия теперь будет записываться по-другому, так как не только появление выборки [math]X^l[/math], но и появление модели [math]\beta[/math] также является случайным. Их совместное появление описывается, согласно формуле условной вероятности, плотностью распределения:

[math]p(X^l, \beta; \gamma)=p(X^l|\beta)p(\beta;\gamma)[/math]

Таким образом, приходим к принципу максимума совместного правдоподобия данных и модели:

[math]L_{\gamma}(\beta, X^l)=\ln p(X^l, \beta;\gamma)=\sum\limits_{i=1}^l \ln p(x_{i}, y_{i}|\beta) + \ln p(\beta; \gamma) \rightarrow max_{\beta}[/math]

Функционал [math]L_{\gamma}[/math] распадается на два слагаемых: логарифм правдоподобия и регуляризатор, не зависящий от данных. Второе слагаемое ограничивает вектор параметров модели, не позволяя ему быть каким угодно.

В итоге мы получили, что с байесовской точки зрения многие методы регуляризации соответствуют добавлению некоторых априорных распределений на параметры модели. При этом можно определить распределения, которые соответствуют представленным ранее [math]L_{1}[/math] и [math]L_{2}[/math] регуляризаторам.

Нормальный регуляризатор

Пусть вектор [math]\beta[/math] имеет нормальное распределение, все его компоненты независимы и имеют равные дисперсии:

[math]\beta \sim N(0, \sigma^2)[/math]

Логарифмируя, получаем квадратичный регуляризатор:

[math]\ln p(\beta; \sigma) = \ln (\frac{1}{(2 \pi \sigma)^{n/2}} \exp(- \frac{\| \beta \| ^ 2}{2 \sigma})) = - \frac{1}{2 \sigma}\| \beta \| ^ 2 + const(\beta),[/math]

где [math]const(\beta)[/math] — слагаемое, не зависящее от [math]\beta[/math], которым можно пренебречь, поскольку оно не влияет на решение оптимизационной задачи. В итоге имеем [math]L_{2}[/math] — регуляризатор.

Лапласовский регуляризатор

Пусть вектор [math]\beta[/math] имеет распределение Лапласа, все его компоненты независимы и имеют равные дисперсии:

[math]\beta \sim Laplace(0, C)[/math]

Тогда:

[math]\ln p(\beta; C) = \ln (\frac{1}{(2C)^n} \exp(- \frac{\| \beta \|_{1}}{C})) = - \frac{1}{C}\| \beta \|_{1} + const(\beta), \| \beta \|_{1} = \sum\limits_{j}|\beta_{j}|[/math]

Распределение Лапласа имеет более острый пик и более тяжёлые «хвосты», по сравнению с нормальным распределением. Его дисперсия равна [math]2C^2[/math].

Аналогично случаю с нормальным регуляризатором, [math]const(\beta)[/math] можно опустить и, таким образом, получаем [math]L_{1}[/math] — регуляризатор.

Регуляризация в линейной регрессии

В линейной регрессии моделируется линейная зависимость между зависимой и независимой переменной. Таким образом, модель алгоритмов для нее состоит из функций вида:

$g(x, \beta) = \sum\limits_{j}^n \beta_{j} f_{j}(x)$

В итоге оптимизируемый функционал эмпирического риска выглядит следующим образом:

$Q(a) = \|F\beta - y\|^2$,

где $F = (f_{x_{i}})_{l \times n}$ — матрица объекты-признаки, $y = (y_{i})_{l \times 1}$ — целевой вектор, $\beta = (\beta_{j})_{n \times 1}$ — вектор параметров. Приравняв нулю производную $Q(\beta)$ по параметру $\beta$, получаем:

$\beta^* = (F^TF)^{-1}F^Ty$

В итоге, использовав сингулярное разложение для представления $F$ и проведя МНК-аппроксимизацию целевого вектора $y$, имеем выражение для нормы вектора \beta:

$\|\beta^*\|^2 = \sum\limits_{j=1}^n \frac{1}{\lambda_{j}}(v_{j}^Ty)^2$

К сожалению, могут возникнуть проблемы мультиколлинеарности и переобучения в случае, если ковариационная матрица $\sum = F^T F$ плохо обусловлена. Одним из способов борьбы с этими проблемами является регуляризация.

В статье о видах регрессии представлены модификации линейной регресиии с различными регуляризаторами ($L_{1}$ и $L_{2}$) и их отличие. Описание в данном разделе будет похожим, однако здесь будет рассмотрен эффект от добавления регуляризаторов немного детальнее.

Гребневая регрессия

К функционалу $Q$ добавляется $L_{2}$-регуляризатор.

Итоговый минимизируемый функционал с поправкой:

[math]Q_{\lambda}(\beta) = ||F \beta - y||^2 + \lambda ||\beta||^2[/math]

Итоговое выражение для параметра \beta:

[math]\beta_{\tau}^* = (F^TF + \tau I_{n})^{-1}F^Ty[/math]

Таким образом, перед обращением матрицы к ней добавляется "гребень" — диагональная матрица $\tau I_{n}$. При этом все её собственные значения увеличиваются на $\tau$, а собственные векторы не изменяются. В результате матрица становится хорошо обусловленной, оставаясь в то же время «похожей» на исходную.

Рассмотрим, какой эффект оказывает добавление гребня. Выразим регуляризованное МНК-решение через сингулярное разложение:

$\beta_{t}^* = (UD^2U^T + \tau I_{n})^{-1}UDV^{T}y=U(D^2+\tau I_{n})^{-1}DV^Ty=\sum\limits_{j=1}^n \frac{\sqrt{\lambda_{j}}}{\lambda_{j} + \tau}u_{j}(v_{j}^Ty)$

Теперь найдём регуляризованную МНК-аппроксимацию целевого вектора y:

$F \beta_{\tau}^* = VDU^T \beta_{\tau}^* = V diag(\frac{\lambda_{j}}{\lambda_{j} + \tau})V^Ty = \sum\limits_{j=1}^n \frac{\lambda_{j}}{\lambda_{j} + \tau}v_{j}(v_{j}^Ty)$

Как можно видеть, проекции на собственные векторы сокращаются, умножаясь $\frac{\lambda_{j}}{\lambda_{j} + \tau} \in (0, 1)$.

В сравнении с нерегуляризованным случаем, уменьшается и норма вектора $\beta$:

$\|\beta_{\tau}^*\|^2 = \| D^2(D^2 + \tau I_{n})^{-1}D^{-1}V^{T}y)\|^2 = \sum\limits_{j=1}^n \frac{1}{\lambda_{j} + \tau}(v_{j}^Ty)^2 < \sum\limits_{j=1}^n \frac{1}{\lambda_{j}}(v_{j}^Ty)^2 = \|\beta^*\|^2$

Поэтому данный метод называют также сжатие или сокращение весов.

Из формул видно, что по мере увеличения параметра $\tau$ вектор коэффициентов $\beta_{\tau}^*$ становится всё более устойчивым и жёстко определённым. Фактически, происходит понижение эффективной размерности решения — это второй смысл термина сжатие. Роль размерности играет след проекционной матрицы.

В нерегуляризованном случае:

$n_{effective} = tr\:F(F^TF)^{-1}F^T = tr(F^TF)^{-1}F^TF = tr\:I_{n} = n$

В случае с гребнем:

$n_{effective} = tr\:F(F^TF + \tau I_{n})^{-1}F^T = tr\:diag(\frac{\lambda_{j}}{\lambda_{j} + \tau}) = \sum\limits_{j=1}^n \frac{1}{\lambda_{j}} < n$

Лассо регрессия

К функционалу $Q$ добавляется $L_{1}$-регуляризатор.

Итоговый минимизируемый функционал с поправкой:

[math]Q_{\tau}(\beta) = ||F \beta - y||^2 + \tau ||\beta||[/math]

Запишем систему для этой регрессии в виде минимизации неизменного функционала $Q$ при неравенстве-ограничении:

$\begin{cases} Q(\beta) = \| F\beta - y \|^2 \rightarrow min_{\beta} \\ \sum\limits_{j=1}^n|\beta_{j}| \leq \chi \\ \end{cases}$

Так как используется $L_{1}$-регуляризатор, коэффициенты $\beta_{j}$ постепенно обнуляются с уменьшением $\chi$. Происходит отбор признаков, поэтому параметр $\chi$ называют еще селективностью. Параметр $\chi$ "зажимает" вектор коэффициентов $\beta$, отсюда и название метода — лассо (англ. LASSO, least absolute shrinkage and selection operator).

Сравнение гребниевой и лассо регрессий

Основное различие гребниевой и лассо регрессий заключается в том, что первая может приводить к обращению некоторых независимых переменных в ноль (используется $L_{1}$-регуляризатор), тогда как вторая уменьшает их до значений, близких к нулю (используется $L_{2}$-регуляризатор).

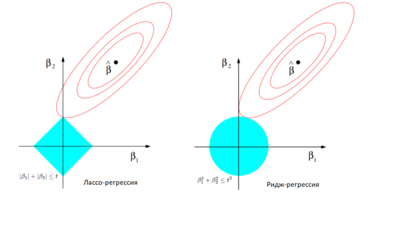
Продублируем наглядный пример из статьи о вариациях регрессии. Рассмотрим для простоты двумерное пространство независимых переменных. В случае лассо регрессии органичение на коэффициенты представляет собой ромб ([math]|\beta_1| + |\beta_2| \leq t[/math]), в случае гребневой регрессии — круг ([math]\beta_1^2 + \beta_2^2 \leq t^2[/math]). Необходимо минимизировать функцию ошибки, но при этом соблюсти ограничения на коэффициенты. С геометрической точки зрения задача состоит в том, чтобы найти точку касания линии, отражающей функцию ошибки с фигурой, отражающей ограничения на [math]\beta[/math]. Из Рис. 3 интуитивно понятно, что в случае лассо регрессии эта точка с большой вероятностью будет находиться на углах ромба, то есть лежать на оси, тогда как в случае гребневой регрессии такое происходит очень редко. Если точка пересечения лежит на оси, один из коэффициентов будет равен нулю, а значит, значение соответствующей независимой переменной не будет учитываться.

Рис.3. Сравнение гребневой и лассо регрессий, пример для двумерного пространства независимых переменных. Бирюзовые области изображают ограничения на коэффициенты [math]\beta[/math], эллипсы — некоторые значения функции наименьшей квадратичной ошибки.

Также полезно будет рассмотреть простую модельную задачу. Пусть $l = n$ и матрица объекты-признаки является единичной $F = I$. Тогда МНК-решение дает вектор коэффициентов $\beta$:

$\beta^* = argmin(\sum\limits_{i=1}^l(\beta_{i} - y_{i})^2)$

$\beta_{j}^* = y_{j}$

В случае с гребниевой регрессией:

$\beta_{j}^* = \frac{y_{j}}{1 + \lambda}$

В случае с лассо регрессией:

$\beta_{j}^* = \begin{cases} y_{j} - \lambda / 2, y_{j} > \lambda / 2 \\ y_{j} + \lambda / 2, y_{j} < -\lambda / 2 \\ 0, |y_{j}| \leq \lambda / 2 \end{cases}$

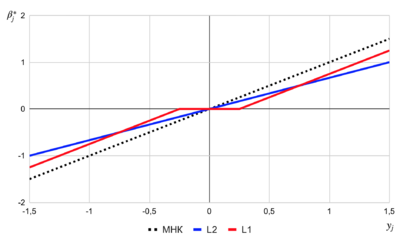
В итоге на Рис. 4 на графиках с зависимостями $\beta_{j}^*$ от $y_{j}$ можно увидеть описанные ранее особенности данных регуляризованных линейных регрессий.

Рис.4. Сравнение гребневой и лассо регрессий, пример для простой модельной задачи.

Регуляризация в алгоритмах

Градиентный спуск

Алгоритм градиентного спуска используют для нахождения аппроксимирующей зависимости, определяя вектор весов [math]w \in R^n[/math], при котором достигается минимум эмпирического риска:

[math]Q(w, X^l)=\sum\limits_{i=1}^l\mathcal{L}(y_{i}, \langle w, x_{i} \rangle) \rightarrow min_{w}[/math]

В этом методевыбирается некоторое начальное приближение для вектора весов [math]w[/math], затем запускается итерационный процесс, на каждом шаге которого вектор w изменяется в направлении наиболее быстрого убывания функционала Q — противоположно вектору градиента [math]Q'(w)=(\frac{\partial Q^(w)}{\partial w_{j}})_{j=1}^n[/math]:

[math]w := w - \eta Q'(w)[/math],

где [math]\eta \gt 0[/math] — величина шага в направлении антиградиента.

Регуляризация — одна из эвристик улучшения градиентных методов обучения. Основным способом уменьшить переобучение является квадратичная регуляризация, называемая также сокращением весов. Чтобы ограничить рост абсолютных значений весов, к минимизируемому функционалу [math]Q(w)[/math] добавляется штрафное слагаемое:

[math]Q_{\tau}(w) = Q(w) + \frac{\tau}{2}\|w\|^2[/math]

Это приводит к появлению аддитивной поправки в градиенте:

[math]Q′τ (w) = Q′(w) + \tau[/math]

В результате правило обновления весов принимает вид:

[math]w := w(1 - \eta \tau) - \eta Q'(w)[/math]

Таким образом, вся модификация сводится к появлению неотрицательного множителя [math](1 − \eta \tau)[/math], приводящего к постоянному уменьшению весов.

Регуляризация предовтращает паралич, повышает устойчивость весов в случае мультиколлинеарности, повышает обобщающую способность алгоритма и снижает риск переобучения. Однако есть и недостатки — параметр [math]\tau[/math] необходимо выбирать с помощью кросс-валидации, что связано с большими вычислительными затратами.

Метод опорных векторов

Метод опорных векторов (SVM) используется для задач классификации и регрессии. В нем строится гиперплоскость, разделяющая объекты выборки оптимальным образом.

К сожалению, зачастую выборка является линейно неразделимой. В таком случае приходится "ослаблять ограничения", позволяя некоторым объектам попадать на территорию другого класса. Для каждого объекта от отступа отнимается некоторая положительная величина $\xi_i$, но требуется, чтобы введенные поправки были минимальны. В итоге постановка задачи SVM с мягким отступом (англ. soft-margin SVM) выглядит следующим образом: $\begin{cases} \frac{1}{2} \lVert w \rVert^2 + C \sum\limits_{i=1}^l \xi_i \to \min\limits_{w, b, \xi} \\ M_i(w, b) \geq 1 - \xi_i, \quad i = 1, \ldots, l \\ \xi_i \geq 0, \quad i = 1, \ldots, l \\ \end{cases}$

Как показано в соответствующем данному алгоритму разделе, эквивалентной задачей безусловной минимизации является: $Q(w, b) = \frac{1}{2C} \lVert w \rVert^2 + \sum\limits_{i=1}^l \left(1 - M_i(w, b)\right)_+ \to \min\limits_{w, b}$

В силу неравенства $[M_{i} < 0] \leq (1 - M_{i})_{+}$, функционал $Q(w, b)$ можно рассматривать как верхнюю оценку эмпирического риска, к которому добавлен регуляризатор $\frac{1}{2C} \|w\|^2$.

С введением регуляризатора устраняется проблема мультиколлинеарности, повышается устойчивость алгоритма, улучшается его обобщающая способность.

В результате получаем, что принцип оптимальной разделяющей гиперплоскости или максимизации ширины разделяющей полосы в случае неразделимой выборки тесно связан с $L_{2}$-регуляризацией, которая возникает естественным образом из постановки задачи.

Также существуют разновидности SVM с другими регуляризаторами.

• Метод релевантных векторов (англ. RVM, Relevance vector Machine):

$\frac{1}{2}\sum\limits_{i=1}^l(\ln w_{i} + \frac{\lambda_{i}^2}{w_{i}})$

• Метод опорных векторов с лассо (англ. LASSO SVM):

$\mu \sum\limits_{i=1}^n|w_{i}|$

• Метод опорных признаков (англ. Support feature machine):

$\sum\limits_{i=1}^nR_{\mu}(w_{i}), \begin{cases} 2 \mu |w_{i}|, |w_{i}|<\mu \\ \mu^2 + w_{i}^2, |w_{i}| \geq \mu \end{cases}$

Другие использования регуляризации

Логистическая регрессия

Как было показано в мотивационном примере, для логистической регрессии полезно использовать регуляризацию.

Для настройки вектора коэффициентов $\beta$ по обучающей выборке $X^l$ максимизируют логарифм правдоподобия:

$L(\beta, X^l) = log_{2}\prod\limits_{i=1}^lp(x_{i}, y_{i}) \rightarrow max_{\beta}$

$L(\beta, X^l) = \sum\limits_{i=1}^{l}log_{2}\sigma(\langle \beta, x_{i} \rangle y_{i}) + const(\beta) \rightarrow max_{\beta}$

$L_{2}$-регуляризация:

$L(\beta, X^l) = \sum\limits_{i=1}^{l}log_{2}\sigma(\langle \beta, x_{i} \rangle y_{i}) - \lambda \| \beta \|^2 + const(\beta) \rightarrow max_{\beta}$

$L_{1}$-регуляризация:

$L(\beta, X^l) = \sum\limits_{i=1}^{l}log_{2}\sigma(\langle \beta, x_{i} \rangle y_{i}) - \lambda \|\beta \|_{1} + const(\beta) \rightarrow max_{\beta}$

Аналогично можно использовать и другие регуляризаторы.

Нейронные сети

Регуляризация также используется и в нейронных сетях для борьбы со слишком большими весами сети и переобучением. Однако, в этом случае зануление коэффициентов при использовании $L_{1}$-регуляризатора не несет в себе смысл "отбора признаков", как в случае с линейными моделями. Регуляризация не снижает число параметров и не упрощает структуру сети.

Для нейронной сети помимо добавления "штрафного" слагаемого к эмпирическому риску используют и другой метод регуляризации — прореживание сети (англ. dropout), в ходе которого упрощают сеть, руководствуясь правилом — если функция ошибки не изменяется, то сеть можно упрощать и дальше. Подробнее об этом можно почитать в статье, рассказывающей о практике реализации нейронных сетей.

См. также

• Переобучение
• Модель алгоритма и её выбор
• Байесовская классификация
• Вариации регрессии
• Линейная регрессия
• Логистическая регрессия
• Стохастический градиентный спуск
• Метод опорных векторов (SVM)
• Нейронные сети, перцептрон
• Практики реализации нейронных сетей

Источники информации

• Воронцов К.В. — Математические методы обучения по прецедентам
• Википедия — Регуляризация (математика)
• coursea.org — Регуляризация
• machinelearning.ru — L1-регуляризация линейной регрессии
• medium.com — 5 видов регрессии и их свойства
• Wikipedia — Elastic net regularization
• Keng B. — A Probabilistic Interpretation of Regularization