Дополнение к ранжированию

Порядки

При рассмотрении различных ситуаций, связанных с извлечением экспертных знаний, возникает потребность каким-либо упорядочить все множество оценок, затрагивая уже понятие группового ранжирования. Положим, имеется конечное множество Χ объектов (например, экспертных оценок или критериев) и m экспертов, пронумерованных индексами 1,2... m. каждый i-й эксперт выставляет рейтинг, порождая порядок.

Слабое ранжирование.Представления

Слабое упорядовачивание

Определение:

Бинарное отношение [math]\lt [/math] на множестве [math]X x X[/math], которое является частично упорядоченным, называется слабым упорядочиванием (англ. weak ordering), если оно обладает следующими свойствами: Иррефлексивность (англ. irreflexivity): [math]\forall a \in X:[/math] если [math]a \lt b[/math], то [math]b \lt a[/math] - не выполняется. Ассиметричность (англ. asymmetry): [math]\forall a, b \in X:[/math] если [math]a \lt b[/math], то не [math] b \lt a [/math]. Транзитивность (англ. transitivity): [math]\forall a, b, c \in X:[/math] если [math]a\lt b[/math] и [math]b\lt c[/math], то [math]a\lt c[/math]. Транзитивность несравнимости (англ. transitivity of incomparability): [math]\forall a, b, d \in X:[/math] если [math]a[/math] несравнимо с [math]b[/math], и [math]b[/math] не сравнимо с [math]d[/math], то [math]a[/math] несравнимо с [math]d[/math]. Примечание: Строгое определение несравнимости: [math]\forall a, b \in X:[/math], если [math]¬b\lt a[/math] и [math]¬a\lt b[/math] и [math]a\not=b[/math], то [math]a\sim b[/math].

Рассмотрим случаи, определеяющее частичное упорядочение как:

• Сильное: [math]\forall a, b \in X:[/math] [math]a \lt b[/math] и [math]b \lt a[/math], те если ~ [math]\emptyset[/math].
• Слабое: [math]\forall a, b, c \in X:[/math] если [math]a\sim b\sim c[/math], то [math]a\sim b[/math] и [math]a=c[/math].

Можно заключить, что любое cильное упорядовачивание есть слабое. Отношение несравнимости является отношением эквивалентности для всех своих разбиений на множестве [math]X[/math], что являются линейно упорядоченными.

Сильный подпорядок

Определение:

Сильный подпорядок — такой подпорядок, на котором присутствует отношение связанности.

Сильный подпорядок [math]≤ \in XxX[/math] обладает рядом следующих свойств:

• Транзитивность: [math]\forall a, b, c \in X:[/math], если [math]a≤b[/math] и [math]b≤c \Rightarrow a≤c[/math].
• Связанности: [math]\forall a, b \in X:[/math]выполнимо либо [math]a≤b[/math], либо [math]b≤a[/math].

Если в любом сильном подпорядке [math]\exists a,b : a≤b[/math] и [math]b≤a[/math], то на нем определено отношение эквивалентности. Поскольку операция определена для всех элементов, такие подпорядки еще называют отношением предпочтения.

Упорядоченное разбиение

Сравнения

Вещественная функция

Удобство использования слабого ранжирования в том, что его элементы могут быть представленны единственным образом с помощью вещественных функций. Рассмотрим следующую теорему.

Теорема:

Для любого частичного упорядовачивания [math]\lt \in XxX[/math] слабое тогда и только тогда, когда существует [math]\lt _t\in YxY[/math] и отображение [math] u: X \rightarrow Y :[/math] если [math]a\lt b[/math], то [math]u(a) \lt _t u(b)[/math] и наоборот.

Таким образом, чтобы имели место быть:

• частичный подпорядок: для [math]a≤b[/math] тогда и только тогда, когда [math]u(a)≤u(b)[/math].
• эквивалентность: для [math]a \sim b[/math] тогда и только тогда, когда [math]u(a)=u(b)[/math].

Ограничения:

- Лексикографические предпочтения

 Хоть и на любом конечном множестве может определена ранжирующая функция, однако для случая лексикографического порядка функция не определена на [math]R^n[/math]. 

- Инъективность

 В случае, если бы [math]u[/math] являлась бы инъективной функцей, что класс эквивалентности двух элементов множества [math]Y[/math] мог бы переходить в более широкий соответсвий класс на множестве [math]X[/math].

- Сюрьективность

 Если на [math]u[/math] вводятся ограничения, чтобы быть сюръективной функцией, то при отображении элементов некого класса на [math]Y[/math] возможно соответсвие ему меньшего или вовсе пустого класса на [math]X[/math]. 

Кусочная последовательность

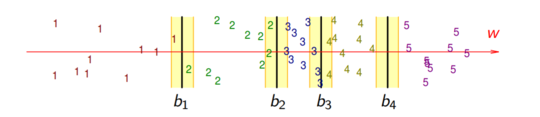
Для любого конечного множества [math]X[/math], на котором задано отношение слабого упорядовачивания и [math]\exists u: X \rightarrow Y [/math], может быть применимо моделирование с помощью кусочных последовательностей. Рассмотрим пример. Положим, что

[math]X=\{ a, b, c, d, e \}[/math][math]u(a) = u(c) = 0, u(e) = 2, u(b) = u(d) = 5[/math]

Тогда слабое ранжирование [math]\lt [/math] представляется в виде следующего:

[math]\{ a, c \} \{ e \} \{ b, d \} [/math]

Supervised алгоритмы ранжирования

OC-SVM

Ordinal Classification SVM - алгоритм поточечного ранжирования, рассматривающий каждый объект обособленно. В основе стоит использования идеи метода опорных векторов о проведении разделяющей гиперплоскости над множеством оценок.

Постановка задачи

Пусть имеется некое число градаций (оценок, предпочтений) [math]K[/math], тогда [math]Y=\{1,2 ...K\}[/math] — ранжирующая функция с порогами [math]b_0=-\infty[/math], [math]b_1,b_2 ...b_(K-1) \in R, b_k=\infty:[/math] [math]a(x)=y[/math], если [math]b_(y-1)\lt (w,x)\le b_y [/math]

Основное отличие от классического подхода в том, что на имеющееся [math]K[/math] границ необходимо найти [math]K-1[/math] зазоров. Иными словами, необходимо найти один направляющий вектор [math]K-1[/math] числа гиперплоскостей. Исходим от предположения, что найдется такое направление, в котором объекты удовлетворительно отранжировались.

Направляющий вектор для K=5

Подход

Поскольку теперь увеличилось число зазоров, классического значения штрафа [math]\xi[/math] недостаточно — необходимы штрафы [math]\xi^*_i[/math] и [math]\xi_i[/math] для нарушение с левой и правой сторон соответственно [math]i-[/math]ой границы. Ограничительное условие для такого случая состоит в том, что произвольный объект [math]x_i[/math], оказавшийся между разделяющими полосами, не должен выйти за их пределы ни слева, ни справа, что можно записать как:

[math]b_{y_i-1}+1-\xi^*_i \le \langle w_i,x_i\rangle \le b_{y_i}-1+\xi_i [/math]

Для случая крайних границ, для объектов [math]x_i : \hat{K}=1[/math] может существовать только нарушение слева от границы, когда для объектов [math]x_i : \hat{K}=K[/math] — только справа от границы. Таким образом, задача может быть сформирована как задача минимизации с ограничениями:

[math] \begin{cases} 1/2||w||^2 + C\sum_{i=1}^l(\xi^*_i[y_i \ne 1] + \xi_i[y_i \ne K]) \rightarrow \underset{w,b,\xi}{min} ; \\ b_{y_i-1}+1-\xi^*_i \le \langle w_i,x_i\rangle \le b_{y_i}-1+\xi_i ; \\ \xi^*_i \ge 0, \xi_i \ge 0 \end{cases} [/math]

Ranking SVM

Алгоритм для попарного подхода к ранжированию. Основное отличие от алгоритма SVM в том, что теперь объекты нумеруются попарно.

Постановка задачи

Считаем, что теперь решаем следующую оптимизационную задачу:

<tex>Q(a) = \frac{1}{2} === Lambda Rank ===