Neural Style Transfer
Описание алгоритма NST
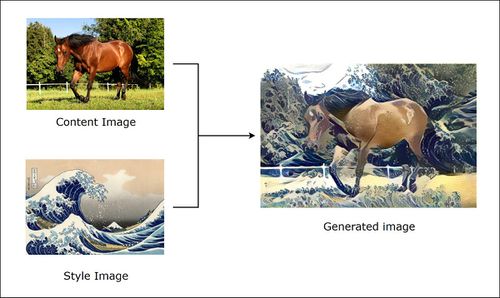
Алгоритм нейронного переноса стиля[1] (англ. Neural Style Transfer, NST), разработанный Леоном Гатисом, Александром Экером и Матиасом Бетге, преобразует полученное на вход изображение в соответствии с выбранным стилем. Алгоритм берет два изображения:
- Изображение контента (англ. Content Image), в котором нас интересует содержание. Обычно оно является фотографией.
- Изображение стиля (англ. Style Image), в котором нас интересует художественный стиль (цветовое наполнение, текстуры и т.д.). Обычно изображением стиля являются картины известных художников.
Затем алгоритм изменяет входные данные так, чтобы они соответствовали содержанию изображения контента и художественному стилю изображения стиля. Авторами в качестве модели сверточной нейронной сети предлагается использовать сеть VGG16.
История алгоритма NST
Обзор предыдущих методов
До появления NST исследования расширились вокруг области, называемой нефотореалистичным рендерингом (non-photorealistic rendering, NPR). В настоящее время это твердо установленная область в сообществе компьютерной графики. Однако большинство алгоритмов NPR стилизации обычно сильно зависят от конкретных художественных стилей (например, масляные картины, анимация), которые они имитируют, и эти алгоритмы не могут быть легко расширены для получения стилизованных результатов для других художественных стилей.
В отличие от NST, алгоритмы NPR не используют нейронные сети. Рассмотрим некоторые NPR-алгоритмы без CNN, a именно NPR-алгоритмы художественного рендеринга 2D-изображений, который называется художественным рендерингом на основе изображений (image-based artistic rendering, IB-AR):
Stroke-Based Rendering
Рендеринг на основе штрихов (SBR) относится к процессу размещения виртуальных штрихов (например, мазков кистью, фрагментов, штрихов) на цифровом холсте для визуализации фотографии с определенным стилем. Процесс SBR, как правило, начинается с исходной фотографии, поэтапно комбинируя мазки для соответствия фотографии и, наконец, создает нефотореалистичные изображения, которые выглядят как фотография, но с художественным стилем (Рис. 2).
SBR обычно эффективен при моделировании определенных типов стилей (например, масляной живописи, акварели, эскизов). Однако каждый алгоритм SBR тщательно спроектирован только для одного конкретного стиля и не способен моделировать произвольный стиль, который не является гибким.
Region-Based Techniques
Рендеринг на основе регионов (RBT) должен включать сегментацию регионов, чтобы обеспечить адаптацию рендеринга на основе контента в регионах. Алгоритмы RBT используют форму регионов для определения расположения штрихов. Таким образом, различные образцы штрихов могут быть созданы в разных семантических областях изображения (Рис. 3).
Учет регионов при рендеринге позволяет осуществлять локальный контроль над уровнем детализации. Однако проблема SBR сохраняется: RBT не способен имитировать произвольный стиль.
Example-Based Rendering
Рендеринга на основе примеров (EBR) изучает соответствия между образцовой парой, то есть соответствия между исходными и целевыми стилизованными изображениями под наблюдением. Обучающий набор содержит пары не стилизованных исходных изображений и соответствующие стилизованные изображения с определенным стилем. Алгоритм аналогии изображений затем изучает аналогичное преобразование из примерных обучающих пар и создает аналогичные стилизованные результаты при получении тестовой входной фотографии.
В целом, аналогии с изображениями эффективны для различных художественных стилей. Однако пары тренировочных данных обычно недоступны. К тому же аналогии изображений используют низкоуровневые функции, которые не позволяют эффективно захватывать контент и стиль, что ограничивает производительность.
Происхождение NST
Несмотря на то, что некоторые алгоритмы IB-AR без CNN способны точно отображать определенные предписанные стили, они обычно имеют ограничения в гибкости, разнообразии стилей и эффективном извлечении структуры изображения. Следовательно, существует потребность в новых алгоритмах для устранения этих ограничений, что порождает область NST.
Леон Гатис первый, кто изучил, как использовать CNN для воспроизведения известных стилей рисования на естественных изображениях. Он предложили смоделировать контент фотографии в качестве ответа функции от предварительно обученного CNN, а затем смоделировать стиль художественного произведения в качестве сводной статистики функции. Его эксперименты показали, что CNN способен извлекать информацию о содержании из произвольной фотографии и информацию о стиле из произведения искусства. На основании этого открытия Гатис впервые предложил использовать активацию функции CNN для рекомбинации содержания данной фотографии и стиля известных произведений искусства. Основная идея его алгоритма состоит в том, чтобы итеративно оптимизировать изображение с целью сопоставления желаемых распределений функций CNN, которые включают в себя как информацию о содержании фотографии, так и информацию о стиле произведения искусства.
Принцип работы алгоритма NST
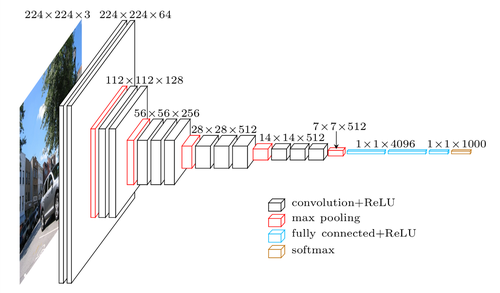
Рассмотрим 1-й сверточный слой (англ. convolution layer) VGG16, который использует ядро 3x3 и обучает 64 карты признаков (англ. feature map) для генерации представления изображения размерности 224x224x64, принимая 3-канальное изображение размером 224x224 в качестве входных данных (Рисунок 2). Во время обучения эти карты признаков научились обнаруживать простые шаблоны, например, такие как прямые линии, окружности или даже не имеющие никакого смысла для человеческого глаза шаблоны, которые тем не менее имеют огромное значение для этой модели. Такое "обнаружение" шаблонов называется обучением представления признаков. Теперь давайте рассмотрим 10-й сверточный слой VGG16, который использует ядро 3x3 с 512 картами признаков для обучения и в итоге генерирует вывод представления изображения размерности 28x28x512. Нейроны 10-го слоя уже могут обнаруживать более сложные шаблоны такие как, например, колесо автомобиля, окно или дерево и т.д.
Собственно вышеперечисленные свойства характерны для любой сверточной нейронной сети, работа которой обычно интерпретируется как переход от конкретных особенностей изображения к более абстрактным деталям вплоть до выделения понятий высокого уровня. При этом сеть самонастраивается и вырабатывает необходимую иерархию абстрактных признаков (последовательности карт признаков), фильтруя маловажные детали и выделяя существенное.
Такая природа представления кодирования сама по себе является ключом к передаче стиля, который используется для вычисления функции потерь между сгенерированным изображением относительно изображения контента и изображения стиля. При обучении модели более десяти тысяч изображений на класс модель может генерировать аналогичное представление признаков для множества различных изображений, если они принадлежат к одному классу или имеют схожий контент или стиль.
Следовательно, имеет смысл использовать разницу в значении представления признаков сгенерированного изображения по содержанию и по стилю изображения, чтобы направлять итерации, через которые мы производим само сгенерированное изображение, но как убедиться, что изображение с контентом C и сгенерированное изображение G похожи по своему содержанию, а не по стилю, в то время как сгенерированное изображение наследует только похожее представление стиля изображения стиля S, а не само изображение стиля в целом. Это решается разделением функции потерь на две части: одна — потеря контента, а другая — потеря стиля.
Производные NST
Чтобы автоматически передать художественный стиль, первая и самая важная проблема заключается в том, как смоделировать и извлечь стиль из изображения. Так как стиль очень связан с текстурой, простой способ - связать визуальное моделирование стилей (англ. Visual Style Modelling) с ранее хорошо изученными методами визуального моделирования текстур (англ. Visual Texture Modelling). После получения представления стиля следующая проблема состоит в том, как восстановить изображение с информацией о желаемом стиле, сохранив его содержимое, что решается с помощью методов восстановления изображения (англ. Image Reconstruction techniques).
Visual Texture Modelling
Parametric Texture Modelling with Summary Statistics
Одним из путей к моделированию текстуры является сбор статистики изображения из образца текстуры и использование сводных статистических свойств для моделирования текстуры. Создается представление на основе Грам для текстур модели, которое представляет собой корреляцию между откликами фильтра в различных слоях предварительно обученной классификационной сети (сеть VGG). Основанное на Грамах кодирует статистику второго порядка набора ответов фильтра CNN.
Предположим, что карта объектов образца изображения текстуры на слое предварительно обученной модели: , где — количество каналов, и — высота и ширина карты объектов .
Тогда представление на основе Грама может быть получено путем вычисления матрицы Грама на карте объектов :
Non-parametric Texture Modelling with Markov Random Fields (MRFs)
Другой известной методологией моделирования текстур является использование непараметрического ресемплирования. Различные непараметрические методы основаны на модели MRF, которая предполагает, что в текстурном изображении каждый пиксель полностью характеризуется своей пространственной окрестностью. Предлагается синтезировать каждый пиксель один за другим путем поиска похожих окрестностей в исходном текстурном изображении и назначения соответствующего пикселя. Ускорить процесс сопоставления окрестностей можно всегда используя фиксированную окрестность.
Image Reconstruction techniques
Реконструкция изображения - это обратный процесс, который заключается в восстановлении всего входного изображения из извлеченного представления изображения. Алгоритмы реконструкции изображения на основе представления CNN:
Image-Optimisation-Based Online Image Reconstruction
Реконструкция изображений на основе оптимизации изображений (IOB-IR). Учитывая обратное представление CNN, алгоритм итеративно оптимизирует изображение (обычно начиная со случайного шума), пока не получит аналогичное желаемое представление CNN. Итеративный процесс оптимизации основан на градиентном спуске в пространстве изображения. Следовательно, процесс занимает много времени, особенно когда желаемое восстановленное изображение является большим.
Model-Optimisation-Based Offline Image Reconstruction
Реконструкция автономных изображений на основе оптимизации моделей (MOB-IR). Для решения проблемы эффективности, было предложено заранее обучить сеть прямой связи и поставить вычислительную нагрузку на этапе обучения. На этапе тестирования обратный процесс может быть просто выполнен с помощью прямого прохода по сети. Это значительно ускоряет процесс восстановления изображения.
Классификация методов NST
Текущие методы NST относятся к одной из двух категорий:
- Image-Optimisation-Based Online Neural Methods (IOB-NST). Эта категория передает стиль путем прямого обновления пикселей в изображении итеративно, основана на методах IOB-IR.
- Model-Optimisation-Based Offline Neural Methods (MOB-NST). Эта категория итеративно оптимизирует генеративную модель и создает стилизованное изображение через один прямой проход, основана на методах MOB-IR.
Image-Optimisation-Based Online Neural Methods
Основная идея алгоритмов IOB-NST состоит в том, чтобы сначала смоделировать и извлечь информацию о стиле и содержимом из соответствующих изображений стиля и содержимого, объединить их в качестве целевого представления, а затем итеративно восстановить стилизованный результат, который соответствует целевому представлению. В целом, разные алгоритмы IOB-NST используют одну и ту же технику IOB-IR, но отличаются тем, как они моделируют визуальный стиль, который основан на категориях методов визуального моделирования текстур.
Общим ограничением алгоритмов IOB-NST является то, что они являются дорогостоящими в вычислительном отношении, из-за итеративной процедуры оптимизации изображения.
Parametric Neural Methods with Summary Statistics
Первый поднабор методов IOB-NST основан на параметрическом моделировании текстуры со сводной статистикой. Стиль характеризуется как набор пространственной сводной статистики.
Алгоритм Гатиса
Согласно тому, что глубокая CNN способна извлекать содержимое изображения из произвольной фотографии и некоторую информацию о внешнем виде из картины, создается компонент контента вновь стилизованного изображения, штрафуя разницу в представлениях высокого уровня, полученных из контента и стилизованных изображений, и дополнительно формируется компонент стиля путем сопоставления сводной статистики стилей и стилизованных изображений на основе Грам из метода моделирования текстур.
Для заданного изображения контента и стиля изображения алгоритм пытается найти стилизованное изображение , которое минимизирует цель:
,
где — потеря контента, сравнивает представление контента данного изображения контента с изображением стилизованного изображения, а — потеря стиля, сравнивает представление стиля на основе Грамы, полученной из изображения стиля, с изображением стилизованного изображения. и используются для баланса компонента контента и компонента стиля в стилизованном результате.
и дифференцируемы. Таким образом, при случайном шуме в качестве начального , это уравнение можно минимизировать, используя градиентный спуск в пространстве изображения с обратным распространением.
Возможные варианты решения проблем алгоритма Гатиса
Алгоритм Гатиса не имеет явных ограничений на тип стилевых изображений, в отличие от предыдущих алгоритмов IB-AR без CNN. Однако алгоритм неэффективно сохраняет согласованность тонких структур и деталей во время стилизации, так как функции CNN неизбежно теряют некоторую информацию низкого уровня. Кроме того, он обычно не подходит для фотореалистичного синтеза из-за ограничений представления стилей на основе Грам. Также он не учитывает изменения мазков кисти, информацию о семантике и глубине, содержащуюся в изображении контента, которые являются важными факторами при оценке качества изображения.
Одним из ограничений алгоритма на основе Грама является его нестабильность во время оптимизаций и ручная настройка параметров. Райзером было обнаружено, что активация функций с совершенно разными средствами и дисперсиями может иметь одну и ту же матрицу Грама, что является основной причиной нестабильности. Поэтому была введена дополнительная потеря гистограммы, которая направляет оптимизацию для соответствия всей гистограмме активаций функции. Также было представлено предварительное решение для автоматической настройки параметров, которое заключается в явном предотвращении градиентов с экстремальными значениями посредством экстремальной нормализации градиента. Путем дополнительного сопоставления гистограммы активаций признаков алгоритм Райзера обеспечивает более стабильную передачу стилей с меньшим количеством итераций и усилий по настройке параметров. Однако его преимущество достигается за счет высокой вычислительной сложности. Кроме того, вышеупомянутые недостатки алгоритма Гатиса все еще существуют, например, недостаток рассмотрения в глубину и согласованность деталей.
Так как функции CNN неизбежно теряют некоторую информацию низкого уровня, содержащуюся в изображении, в стилизованных результатах обычно присутствуют некоторые непривлекательные искаженные структуры и нерегулярные артефакты. Чтобы сохранить согласованность тонких структур во время стилизации, Ли предлагает включить дополнительные ограничения на низкоуровневые элементы в пиксельном пространстве. Он вводит дополнительную потерю Лапласа, которая определяется как квадрат евклидова расстояния между ответами фильтра Лапласа на контентное изображение и стилизованным результатом. Алгоритм Ли имеет хорошую производительность при сохранении тонких структур и деталей во время стилизации. Но ему все еще не хватает соображений в семантике, глубине, вариациях мазков и т. д.
Nonparametric Texture Modelling with MRFs
Алгоритм Ли и Ванда
Непараметрический IOB-NST построен на основе непараметрического моделирования текстуры с помощью MRF. Эта категория рассматривает NST на локальном уровне, то есть работает с патчами, чтобы соответствовать стилю. Метод параметрического NST со сводной статистикой фиксирует только корреляции между элементами пикселей и не ограничивает пространственное расположение, что приводит к менее визуально правдоподобному результату для фотореалистичных стилей. Решение состоит в том, чтобы смоделировать стиль непараметрическим способом и ввести новую функцию потери стиля, которая включает MRF на основе патчей:
,
где — набор всех локальных накладок из карт объектов . обозначает -ую локальную накладку и является наиболее похожим патчем стиля с -тым локальным патчем в стилизованном изображении . Наилучшее соответствие получается путем вычисления нормализованной взаимной корреляции по всем патчам стиля в изображении стиля , — общее количество локальных патчей.
Преимущества и недостатки алгоритма Ли и Ванда
Поскольку алгоритм соответствует стилю на уровне патча, тонкая структура и расположение лучше сохраняются. Преимущество алгоритма состоит в том, что он особенно эффективен для фотореалистичных стилей или, более конкретно, когда фотография и стиль контента похожи по форме и перспективе из-за потери MRF на основе патчей. Однако, как правило, происходит сбой, когда содержимое и стиль изображений имеют сильные различия в перспективе и структуре, поскольку исправления изображения не могут быть правильно сопоставлены. Он также ограничен в сохранении четких деталей и информации о глубине.
Model-Optimisation-Based Offline Neural Methods
MOB-NST решает проблему скорости и вычислительных затрат IOB-NST путем использования MOB-IR для восстановления стилизованного результата, то есть сеть с прямой связью оптимизируется для большого набора изображений для одного или нескольких изображений стиля :
MOB-NST делится на методы:
Per-Style-Per-Model Neural Methods
Parametric PSPM with Summary Statistics
Первые два алгоритма MOB-NST предложены Джонсоном и Ульяновым соответственно. Они имеют схожую идею, заключающуюся в том, чтобы предварительно обучить сеть, ориентированную на стиль прямой связи, и получить стилизованный результат с одним прямым проходом на этапе тестирования. Они отличаются только сетевой архитектурой, для которой дизайн Джонсона примерно соответствует сети, предложенной Рэдвордом, но с остаточными блоками и с извилистыми частями, а Ульянов использовал многомасштабную архитектуру в качестве сети генератора. Целевая функция аналогична алгоритму Гатиса, который указывает, что они также являются параметрическими методами со сводной статистикой.
Алгоритмы Джонсона и Ульянова добились передачи стиля в реальном времени. Тем не менее, конструкция алгоритма в основном следует алгоритму Гатиса, что приводит к аналогичным проблем, что и у Гатиса (например, отсутствие рассмотрения в согласованность деталей и глубины информации).
После Ульянов также обнаружил, что простое применение нормализации к каждому отдельному изображению, а не к пакетной нормализации (англ. batch normalization, BN) приводит к значительному улучшению качества стилизации. Нормализация одиночного изображения называется нормализацией экземпляра (англ. instance normalisation, IN), что эквивалентно нормализации пакета, когда размер пакета = 1. Показано, что сеть передачи стиля с IN сходится быстрее, чем BN, а также обеспечивает визуально лучшие результаты. Одно из объяснений состоит в том, что IN является формой нормализации стиля и может напрямую нормализовать стиль каждого изображения контента до желаемого стиля. Следовательно, цель легче минимизировать, так как остальная часть сети должна заботиться только о потере контента.
Non-parametric PSPM with MRFs
Алгоритм Ли и Ванда решает проблему эффективности, обучая марковскую прямую сеть, используя состязательное обучение. Он представляет собой непараметрический метод на основе патчей с MRF. Показано, что их метод превосходит алгоритмы Джонсона и Ульянова в сохранении связных текстур в сложных изображениях, благодаря патч-дизайну. Однако их алгоритм имеет менее удовлетворительную производительность с неструктурными стилями (например, изображениями лица), поскольку их алгоритм не учитывает семантику. Другие недостатки их алгоритма включают в себя отсутствие учета глубины информации и вариаций мазков кисти, которые являются важными визуальными факторами.
Multiple-Style-Per-Model Neural Methods
Хотя вышеупомянутые подходы PSPM могут создавать стилизованные изображения на два порядка быстрее, чем предыдущие методы IOB-NST, отдельные генеративные сети должны быть обучены для каждого конкретного изображения стиля. Но многие картины (например, картины импрессионистов) имеют одинаковые мазки и отличаются только своей цветовой палитрой и для каждой из них необходимо обучать отдельную сеть. Поэтому предлагается MSPM, который повышает гибкость PSPM путем дальнейшего объединения нескольких стилей в одну модель. Это можно сделать двумя способами:
Привязка только небольшого количества параметров к каждому стилю
Алгоритм Дюмулена. Дюмулен обнаружил, что для моделирования различных стилей достаточно использовать одни и те же сверточные параметры масштабирования и сдвига в слоях IN. Поэтому он предлагает алгоритм обучения условной мульти-стильной сети передачи на основе нормализации условного экземпляра (CIN):
где — активация функции ввода, а — индекс желаемого стиля из набора изображений стилей. Каждый стиль может быть достигнут путем настройки параметров аффинного преобразования. Нормализация статистики объектов с различными аффинными параметрами может нормализовать входное изображение контента для разных стилей. Кроме того, алгоритм Дюмулена также может быть расширен для объединения нескольких стилей в одном стилизованном результате путем объединения аффинных параметров различных стилей.
Другой алгоритм, который следует первому пути MSPM, предложен Чен. Алгоритм Чена явно отделяет стиль и контент, то есть использует отдельные сетевые компоненты для изучения соответствующего контента и информации о стиле.
Недостатком этим алгоритмов является то, что они не учитывают общие ограничения алгоритмов NST, например, отсутствие деталей, семантики, глубины и вариаций мазков кисти.
Объединение стиля и контента в качестве входных данных
Одним из недостатков привязки только небольшого количества параметров к каждому стилю является то, что размер модели, как правило, увеличивается с увеличением количества изученных стилей. Этот способ MSPM устраняет это ограничение, полностью исследуя возможности одной единственной сети и комбинируя контент и стиль в сети для идентификации стиля.
Учитывая N целевых стилей, алгоритм Ли проектирует единицу выбора для стиля, которая представляет собой N-мерный однократный вектор. Каждый бит в блоке выбора представляет определенный стиль в наборе целевых стилей. Для каждого бита в единице выбора сначала выбирают соответствующую шумовую карту из равномерного распределения, а затем подают в подсеть стиля, чтобы получить кодированные признаки соответствующего стиля . Путем подачи конкатенации функций , закодированных в стиле, и функций , закодированных в контенте, в часть декодера сети передачи стиля можно получить желаемый стилизованный результат:
Другой алгоритм Чжана и Дана сначала направляет каждое изображение стиля в стиле, установленном через предварительно обученную сеть VGG, и получает многомасштабные активации функций в разных слоях VGG. Затем многомасштабные объединяются с многомасштабными кодированными функциями из разных уровней в кодере через их предлагаемые слои инспирации, которые предназначены для изменения формы в соответствии с требуемым измерением, а также имеют обучаемую матрицу весов для настройки карт объектов, чтобы помочь минимизировать целевую функцию.
Масштабируемость стилей этого типа MSPM намного меньше, поскольку для нескольких стилей используется только одна сеть. Кроме того, некоторые вышеупомянутые ограничения в первом типе MSPM все еще существуют, то есть алгоритмы второго типа MSPM все еще ограничены в сохранении когерентности тонких структур и информации о глубине.
Arbitrary-Style-Per-Model Neural Methods
Функция потерь
В уравнении выше, чтобы получить общую потерю нужно рассчитать потерю содержимого и потерю стиля , а также и — гиперпараметры, которые используются для определения весов для каждого типа потерь, то есть эти параметры можно представить просто как "рычаги" для управления тем, сколько контента / стиля мы хотим наследовать в сгенерированном изображении.
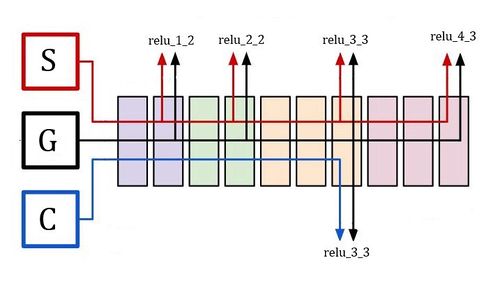
Во время каждой итерации все три изображения, передаются через модель VGG16. Значения функции активации нейронов, которые кодируют представление признаков данного изображения на определенных слоях, принимаются как входные данные для этих двух функций потерь. Также стоит добавить: изначально мы случайным образом инициализируем сгенерированное изображение, например, матрицей случайного шума такого же разрешения, как и изображение контента. С каждой итерацией мы изменяем сгенерированное изображение, чтобы минимизировать общую потерю L.
Функция потери контента
Возьмем функциональное представление 7-го сверточного слоя VGG16. Чтобы вычислить потерю контента, пропускаем изображение контента и сгенерированное изображение через VGG16 и получаем значения функции активации (выходы) 7-го слоя для обоих этих изображений. После каждого сверточного слоя идет ReLU, поэтому мы будем обозначать выход этого слоя в целом как relu_3_3 (поскольку это выход третьего сверточного слоя третьего набора / блока сверток) (Рисунок 2). Наконец, мы находим L2-норму поэлементного вычитания между этими двумя матрицами значений функции активации следующим образом:
, где — тензор выходов слоев сети, — номер сверточного слоя
Это поможет сохранить исходный контент в сгенерированном изображении, а также минимизировать разницу в представлении признаков, которое логически фокусируется на разнице между содержимым обоих изображений.
Функция потери стиля
В отличии от потери контента потерю стиля нельзя рассчитать с помощью разницы значений функции активации нейронов. Необходимо найти корреляцию между значениями функции активации по разным каналам одного и того же слоя. И для этого авторы алгоритма предлагают воспользоваться матрицей Грама.
Матрица Грама
Рассмотрим, как мы передаем наше изображение стиля через VGG16 и получаем значения функции активации из 7-го уровня, который генерирует матрицу представления объектов размером 56x56x256. В этом трехмерном массиве имеется 256 каналов размером 56x56 каждый.
Теперь предположим, что есть канал A, чьи нейроны могут активироваться на изображении, содержащем коричнево-черные полосы, а нейроны канала B — на изображение, содержащее глазное яблоко. Если оба этих канала A и B активируются вместе для одного и того же изображения, то высока вероятность того, что изображение может содержать, например, лицо тигра (поскольку у него было два канала с большими абсолютными значениями, которые активируются для коричнево-черных полос и глазного яблока). Теперь, если оба эти канала будут с большими значениями функции активации, то они будут иметь более высокую корреляцию между каналами A и В, чем между каналами A и С, где канал С активируется на изображении, содержащем ромбовидный шаблон. Чтобы получить корреляцию всех этих каналов друг с другом, нам нужно вычислить нечто называемое матрицей Грама, будем использовать ее для измерения степени корреляции между каналами. Таким образом, именно значение корреляции между каналами служит показателем того, насколько итоговое изображение наследует элементы изображения со стилем.
Функция потерь на основе корреляции матриц Грама
Каждый элемент матрицы Грама содержит меру корреляции всех каналов относительно друг друга. Обозначим матрицу Грама стилевого изображения слоя как , а матрицу Грама сгенерированного изображения того же слоя . Обе матрицы были вычислены из одного и того же слоя, следовательно, с использованием одного и того же числа каналов, что привело к тому, что итоговая матрица размера . Теперь, если мы найдем сумму квадратов разности или L2-норму вычитания элементов этих двух матриц и попытаемся минимизировать ее, то в конечном итоге это приведет к минимизации разницы между изображением стиля и сгенерированным изображением.
В вышеприведенном уравнении представляет номер канала в карте признаков / выходных данных уровня , а представляет карты признаков / выходных данных слоя .
Так как при вычислении потери стиля мы используем несколько уровней активации, это позволяет назначать разные весовые коэффициенты для потери на каждом уровне.
Пример кода на Python
Данный пример реализован на основе открытой платформы глубокого обучения PyTorch
Функция потери контента
class ContentLoss(nn.Module):
def __init__(self, target,):
super(ContentLoss, self).__init__()
# we 'detach' the target content from the tree used
# to dynamically compute the gradient: this is a stated value,
# not a variable. Otherwise the forward method of the criterion
# will throw an error.
self.target = target.detach()
def forward(self, input):
self.loss = F.mse_loss(input, self.target)
return input
Функция потери стиля
def gram_matrix(input):
a, b, c, d = input.size() # a=batch size(=1)
# b=number of feature maps
# (c,d)=dimensions of a f. map (N=c*d)
features = input.view(a * b, c * d) # resize feature maps
G = torch.mm(features, features.t()) # compute the gram product
# we 'normalize' the values of the gram matrix
# by dividing by the number of element in each feature maps.
return G.div(a * b * c * d)
class StyleLoss(nn.Module):
def __init__(self, target_feature):
super(StyleLoss, self).__init__()
self.target = gram_matrix(target_feature).detach()
def forward(self, input):
G = gram_matrix(input)
self.loss = F.mse_loss(G, self.target)
return input
Инициализация модели
cnn = models.vgg19(pretrained=True).features.to(device).eval()
Нормализация
cnn_normalization_mean = torch.tensor([0.485, 0.456, 0.406]).to(device)
cnn_normalization_std = torch.tensor([0.229, 0.224, 0.225]).to(device)
# create a module to normalize input image so we can easily put it in a
# nn.Sequential
class Normalization(nn.Module):
def __init__(self, mean, std):
super(Normalization, self).__init__()
# .view the mean and std to make them [C x 1 x 1] so that they can
# directly work with image Tensor of shape [B x C x H x W].
# B is batch size. C is number of channels. H is height and W is width.
self.mean = torch.tensor(mean).view(-1, 1, 1)
self.std = torch.tensor(std).view(-1, 1, 1)
def forward(self, img):
# normalize img
return (img - self.mean) / self.std
Добавление собственных слоев
# desired depth layers to compute style/content losses :
content_layers_default = ['conv_4']
style_layers_default = ['conv_1', 'conv_2', 'conv_3', 'conv_4', 'conv_5']
def get_style_model_and_losses(cnn, normalization_mean, normalization_std,
style_img, content_img,
content_layers=content_layers_default,
style_layers=style_layers_default):
cnn = copy.deepcopy(cnn)
# normalization module
normalization = Normalization(normalization_mean, normalization_std).to(device)
# just in order to have an iterable access to or list of content/style losses
content_losses = []
style_losses = []
# assuming that cnn is a nn.Sequential, so we make a new nn.Sequential
# to put in modules that are supposed to be activated sequentially
model = nn.Sequential(normalization)
i = 0 # increment every time we see a conv
for layer in cnn.children():
if isinstance(layer, nn.Conv2d):
i += 1
name = 'conv_{}'.format(i)
elif isinstance(layer, nn.ReLU):
name = 'relu_{}'.format(i)
# The in-place version doesn't play very nicely with the ContentLoss
# and StyleLoss we insert below. So we replace with out-of-place
# ones here.
layer = nn.ReLU(inplace=False)
elif isinstance(layer, nn.MaxPool2d):
name = 'pool_{}'.format(i)
elif isinstance(layer, nn.BatchNorm2d):
name = 'bn_{}'.format(i)
else:
raise RuntimeError('Unrecognized layer: {}'.format(layer.__class__.__name__))
model.add_module(name, layer)
if name in content_layers:
# add content loss:
target = model(content_img).detach()
content_loss = ContentLoss(target)
model.add_module("content_loss_{}".format(i), content_loss)
content_losses.append(content_loss)
if name in style_layers:
# add style loss:
target_feature = model(style_img).detach()
style_loss = StyleLoss(target_feature)
model.add_module("style_loss_{}".format(i), style_loss)
style_losses.append(style_loss)
# now we trim off the layers after the last content and style losses
for i in range(len(model) - 1, -1, -1):
if isinstance(model[i], ContentLoss) or isinstance(model[i], StyleLoss):
break
model = model[:(i + 1)]
return model, style_losses, content_losses
Градиентный спуск
def get_input_optimizer(input_img): # this line to show that input is a parameter that requires a gradient optimizer = optim.LBFGS([input_img.requires_grad_()]) return optimizer
Запуск алгоритма
def run_style_transfer(cnn, normalization_mean, normalization_std,
content_img, style_img, input_img, num_steps=300,
style_weight=1000000, content_weight=1):
print('Building the style transfer model..')
model, style_losses, content_losses = get_style_model_and_losses(cnn,
normalization_mean, normalization_std, style_img, content_img)
optimizer = get_input_optimizer(input_img)
run = [0]
while run[0] <= num_steps:
def closure():
# correct the values of updated input image
input_img.data.clamp_(0, 1)
optimizer.zero_grad()
model(input_img)
style_score = 0
content_score = 0
for sl in style_losses:
style_score += sl.loss
for cl in content_losses:
content_score += cl.loss
style_score *= style_weight
content_score *= content_weight
loss = style_score + content_score
loss.backward()
run[0] += 1
if run[0] % 50 == 0:
print("run {}:".format(run))
print('Style Loss : {:4f} Content Loss: {:4f}'.format(
style_score.item(), content_score.item()))
print()
return style_score + content_score
optimizer.step(closure)
# a last correction...
input_img.data.clamp_(0, 1)
return input_img
# run style transfer
output = run_style_transfer(cnn, cnn_normalization_mean, cnn_normalization_std,
content_img, style_img, input_img)