Модели клеточных автоматов

Материал из Викиконспекты
Перейти к: навигация, поиск
Эта статья находится в разработке!

Базовые определения

Определение:
Клеточный автомат[1] представляет собой двусторонне бесконечную ленту, каждая ячейка которой может находиться в некотором состоянии.

Множество состояний $Q$, обозначим состояние ячейки $i$ как $s[i]$.
Изначально все ячейки находятся в состоянии $B \in Q$, кроме ячеек с номерами от $1$ до $n$. Ячейка с номером $i$, где $1 \le i \le n$ находится в состоянии $x_i$, где $x$ - входное слово (будем считать, что $\Sigma \subset Q$, $B \notin \Sigma$).

Правила работы клеточного автомата такие: задано число $d$ и функция $f : Q^{2d+1} \to Q$. За один шаг все клетки меняют состояние по следующему правилу: новое состояние клетки $i$ равно $f(s[i - d], s[i - d + 1], \ldots, s[i + d - 1], s[i + d])$. Если клетка с номером $0$ переходит в состояние $Y$, то автомат допускает слово $x$.

Определение и основные свойства линейного клеточного автомата содержатся в статье "линейный клеточный автомат, эквивалентность МТ".


Определение:
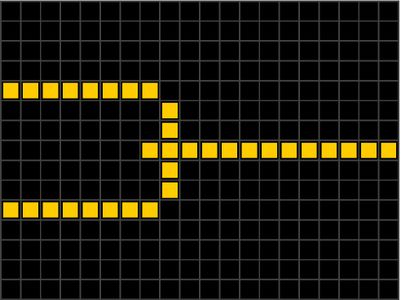
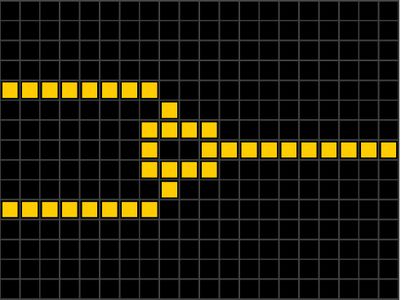
Окрестность Мура[2] ячейки — совокупность ячеек в сетке (двумерном паркете, трёхмерном Евклидовом пространстве, разбитом на равновеликие кубы), имеющих общую вершину с данной ячейкой.
Окрестность Мура порядка [math]r[/math] в двумерном случае представляет собой квадрат со стороной [math]2r + 1[/math][3].


Определение:
Окрестность фон Неймана[4] ячейки — совокупность ячеек в сетке (двумерном паркете, трёхмерном Евклидовом пространстве, разбитом на равновеликие кубы), имеющих общую сторону (грань) с данной ячейкой.


Определение:
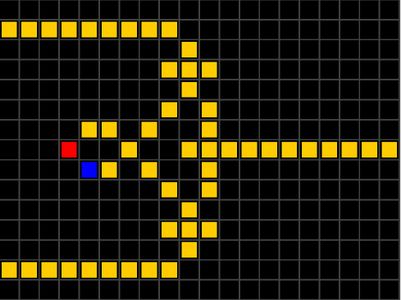
Райский сад[5] — конфигурация КА, которая не может появиться в результате «эволюции», потому что не имеет предшественников.
Теорема (сада Эдема):
Клеточный автомат в евклидовой вселенной является локально инъективным тогда и только тогда, когда он сюръективен.

Другими словами, теорема утверждает, что сады Эдема существуют только в тех автоматах, в которых существуют близнецы.

Данная теорема была выдвинута и доказана Эдвардом Муром[6].

Классификация клеточных автоматов

Классификация Вольфрама

Определение:
Классы Вольфрама[7] — система классификации клеточных автоматов, основанная на их поведении.

Классы, предложенные С. Вольфрамом[8]:

  1. После некоторого количества шагов система стабилизируется — все клетки поля переходят в одинаковое состояние;
  2. Состояния могут быть различными, однако клетки в данном случае образуют наборы статичных или периодических простых структур;
  3. Образуются сложные структуры, характер взаимодействия которых во многих случаях выглядит хаотическим;
  4. Сложные структуры, очень сложное, порой непредсказуемое (хаотичное) взаимодействие.

Классификация Эпштейна

На ряд серьезных недостатков классификации С. Вольфрама указывал[9] Д. Эпштейн.
Один из них состоял в невозможности за разумное время проверить принадлежность клеточного автомата к какому-либо классу для большого числа клеточных автоматов.
В свою очередь он предложил систему классификации двухмерных двоичных клеточных автоматов, призванную выделять кандидатов в универсальные клеточные автоматы.

Классы, предложенные Д. Эпштейном[8]:

  1. Автомат предусматривает расширение объектов поля: в клетке не "зарождается жизнь" при наличии одного "живого" соседа;
  2. Автомат не предусматривает расширения объектов поля: в клетке не "зарождается жизнь" при наличии двух/трех "живых" соседей;
  3. Автомат не предусматривает расширения уменьшения объектов поля: клетка не "умирает" от "перенаселения" или "одиночества";
  4. Автоматы, предусматривающие как расширение, так и уменьшение объектов поля.


Однако, данная классификация так же имела серьезные проблемы, и, в конечном счете, не удовлетворяла своему назначению. Более подробные описания данных классификаций, а также других наиболее распространенных, можно найти в работе П.С. Скакова[8]. В ней, в том числе, были выделены основные достоинства и недостатки различных классификаций, и предложена новая, являющаяся уточнением и модификацией существующих и решающая многие их проблемы.

Одномерные клеточные автоматы

Коды Вольфрама

Определение:
Код Вольфрама — система именования клеточных автоматов (как правило, ЛКА), предложенная С. Вольфрамом в 1983 году[10].
Данная система основана на наблюдении, что таблица, определяющая новое состояние каждой ячейки в автомате, как функция состояний в его окрестности, может интерпретироваться как число из [math]k[/math]-цифр в [math]S[/math]-арной позиционной системе счисления, где [math]S[/math] — число состояний, которое может иметь каждая ячейка в автомате, [math]k = S^{2n + 1}[/math] — число конфигураций окрестности, а [math]n[/math] — радиус окрестности.

В соответствии с определением, код может быть вычислен следующим образом:

  1. Определить все возможные конфигурации состояний окрестности данной ячейки;
  2. Интерпретируя каждую конфигурацию как число, как описано выше, отсортировать их по убыванию;
  3. Для каждой конфигурации определить состояние, которое будет иметь данная ячейка в соответствии с этим правилом на следующей итерации;
  4. Интерпретируя полученный список состояний как [math]S[/math]-арное число, преобразовать это число в десятичное. Полученное десятичное число является кодом Вольфрама.

Далее в статье будут приведены наиболее известные правила.
Все рассматриваемые автоматы представляют собой ЛКА с двумя возможными состояниями. Каждая клетка изменяет своё состояние в зависимости от состояния ее ближайших соседей и ее состояния на предыдущем шаге.

TODO: ADD PICTIRES

Правило 30

Определение:
Правило 30 — ЛКА с двумя состояниями (0 и 1).

Для Правила 30 в таблице даны правила перехода центральной клетки триады в следующее состояние:

Текущее состояние трёх соседних клеток 111 110 101 100 011 010 001 000
Новое состояние центральной клетки 0 0 0 1 1 1 1 0

Так как [math]11110_2 = {30}_{10}[/math], данное правило называется Правилом 30.

Правило 90

Определение:
Правило 90 — ЛКА с двумя состояниями (0 и 1).
Шаг работы автомата состоит в одновременной замене значения в любой ячейке на сумму по модулю 2 её двух соседей.

Правила перехода для Правила 90:

Текущее состояние трёх соседних клеток 111 110 101 100 011 010 001 000
Новое состояние центральной клетки 0 1 0 1 1 0 1 0

Так как [math]1011010_2 = {90}_{10}[/math], данное правило называется Правилом 90.

Правило 110

Определение:
Правило 110 — ЛКА с двумя состояниями (0 и 1).
Шаг работы автомата состоит в одновременной замене значения в любой ячейке на сумму по модулю 2 её двух соседей.

Правила перехода для Правила 110:

Текущее состояние трёх соседних клеток 111 110 101 100 011 010 001 000
Новое состояние центральной клетки 0 1 1 0 1 1 1 0

Так как [math]1101110_2 = {110}_{10}[/math], данное правило называется Правилом 110.

Правило 184

Определение:
Правило 184 — ЛКА с двумя состояниями (0 и 1).

Правила перехода для Правила 184:

Текущее состояние трёх соседних клеток 111 110 101 100 011 010 001 000
Новое состояние центральной клетки 1 0 1 1 1 0 0 0

Так как [math]110111000_2 = {184}_{10}[/math], данное правило называется Правилом 184.

Клеточные автоматы на двумерной решетке

Игра «Жизнь»

Некоторые из приведенных далее определений были взяты с этого[11] сайта, а также со смежных с нем страниц.

Определение:
«Жизнь» — клеточный автомат, представляющий из себя бесконечное клетчатое поле, каждая клетка может быть белой или черной. Состояние, в которое перейдет клетка на следующем шаге, зависит от состояний ее соседей в окрестности Мура.

Дополнительную информацию по игре вы можете найти в статье "игра «Жизнь»".

Состояния

Каждая клетка поля может быть либо белого, либо черного цвета. Белые клетки называются «живыми», черные — «мертвыми».

Правила

На каждом шаге автомата ко всем клеткам применяются следующие правила:

  • В черная клетка, имеющая ровно три белые соседние клетки, становится белой («зарождается жизнь»);
  • Если у белой клетки есть две или три белые соседние клетки, то эта клетка сохраняет свой цвет;
  • Если у белой клетки соседей белого цвета меньше двух или больше трёх, клетка становится черной («умирает от одиночества» или «от перенаселённости»).

Основные элементы

В данном разделе используются термины из «Словаря Жизни»[12].

В зависимости от начального состояния поля, клетки могут образовывать фигуры, обладающие различными свойствами. По этим свойствам принято делить фигуры на следующие классы:

  • Устойчивые фигуры — фигуры, которые остаются неизменными
  • Долгожители — фигуры, которые долго меняются, прежде чем стабилизироваться;
  • Осцилляторы — фигуры, у которых состояние повторяется через некоторое число поколений, большее 1;
  • Двигающиеся фигуры (космические корабли) — фигуры, у которых состояние повторяется, но с некоторым смещением;
  • Ружья — фигуры с повторяющимися состояниями, дополнительно создающие движущиеся фигуры;
  • Паровозы — двигающиеся фигуры с повторяющимися состояниями, которые оставляют за собой другие фигуры в качестве следов;
  • Пожиратели — устойчивые фигуры, которые могут пережить столкновения с некоторыми двигающимися фигурами, уничтожив их;
  • Отражатели — устойчивые или периодические фигуры, способные при столкновении с ними движущихся фигур поменять их направление;
  • Размножители — конфигурации, количество живых клеток в которых растёт как квадрат количества шагов;

Наиболее известные представители данных классов будут рассмотрены далее в статье.

TODO: ADD PICTIRES

Устойчивые фигуры

Устойчивые фигуры или «натюрморты», делятся на несколько классов[13]:

  • Устойчивый образец — объект, который является собственным родителем;
  • Натюрморт — устойчивый объект, являющийся конечным и непустым, из которого нельзя выделить непустую устойчивую часть;
  • Псевдонатюрморт — устойчивый объект, не являющийся натюрмортом, в котором присутствует хотя бы одна мёртвая клетка, имеющая более трёх соседей всего, но меньше трёх соседей в каждом из содержащихся в объекте натюрмортов.

Долгожители

Определение:
Долгожитель — конфигурация из 10 или меньшего числа клеток, которым необходимо не менее 50 поколений для стабилизации[14].


Осцилляторы

Определение:
Осциллятор — конфигурация клеточного автомата, которая после конечного числа поколений повторяется в изначальном виде и положении.


Определение:
Период осциллятора — минимальное число поколений, через которое осциллятор возвращается в исходное состояние.


Двигающиеся фигуры

Определение:
Космический корабль — конфигурация, которая через определённое количество поколений вновь появляется без дополнений или потерь, но со смещением относительно исходного положения.


Определение:
Период космического корабля — минимальное число поколений, за которое космический корабль смещается.


Ружья

Определение:
Ружье — класс конфигураций, у которых основная часть циклически повторяется, как у осцилляторов, а также периодически создаёт космические корабли, которые удаляются от ружья.

У ружья есть два периода: период создания космических кораблей и период повторения состояний ружья.

Паровозы

Определение:
Паровоз — объект, который движется по полю подобно космическому кораблю, но при этом ещё и оставляет за собой след из других объектов.


Определение:
Грабли — паровозы, оставляющие за собой след исключительно из космических кораблей.

Паровозы условно делят на чистые и грязные:

  • Чистый паровоз оставляет след, обладающей легко уловимой на глаз периодичностью;
  • Грязный — сложный, хаотически выглядящий след.

Пожиратели

Определение:
Пожиратель — конфигурация, способная уничтожить космический корабль и восстановиться после контакта.


Отражатели

Определение:
Отражатель — натюрморт или периодическая конфигурация, способная изменить направление движения другой фигуры определенного типа на 90° или 180°, восстанавливая свою структуру после отражения.


Определение:
Время восстановления отражателя — минимальное число поколений, которое должно проходить между столкновением с другими фигурами, чтобы отражатель успевал восстановиться.


Размножители

Определение:
Размножитель — конфигурация, растущая квадратично, производя множество копий вторичной конфигурации, каждая из которых производит множество копий третичной конфигурации.


Существует несколько видов[15] размножителей, отличающихся между собой относительной подвижностью полученных конфигураций. Виды кодируются при сочетаниями трех букв, описывающие, соответственно, первичную, вторичную и третичную конфигурации: Д — движущаяся, Н — неподвижная:

  • НДД — ружьё, вырабатывающее грабли;
  • ДНД — паровоз, вырабатывающий ружья;
  • ДДН — грабли, вырабатывающий паровозы;
  • ДДД — грабли, вырабатывающий грабли.

Райский сад

Теорема сада Эдема применима к «Жизни»: конфигурация, состоящая из одной «живой клетки» переходит в ту же конфигурацию, что и конфигурация, состоящая только из «мертвых» клеток. Следовательно, в «Жизни» существуют сады Эдема.

Wireworld

Определение:
Клеточный автомат Wireworld[16] представляет собой синхронный автомат с двумерной решеткой из квадратов, каждая клетка которой может находиться в одном из четырех состояний.

Состояния

Название состояния Цвет Значение
Пустая клетка Черный Клетка, не занятая проводником
Проводник Желтый По проводнику могут распространяться электроны
Голова электрона Красный Проводник, занятый электроном: вместе с «хвостом электрона» задает направление движения электрона.
Хвост электрона Синий Проводник, занятый электроном: вместе с «головой электрона» задает направление движения электрона.

Правила

На каждом шаге автомата ко всем клеткам применяются следующие правила:

  1. Клетка, находящаяся в состоянии «голова электрона» переходит в состояние «хвост электрона».
  2. Клетка, находящаяся в состоянии «хвост электрона» переходит в состояние «проводник».
  3. Клетка, находящаяся в состоянии «проводник» переходит в состояние «голова электрона», в том случае, если среди соседних клеток ровно одна или две находятся в состоянии «голова электрона».

Общие закономерности

Движение "электрона" в "цепи" происходит со следующими закономерностями:

  • При прохождении электроном разветвления "цепи", в каждое из новых направлений уходит по "электрону";
  • При одновременном столкновении двух и более "электронов", они исчезают.
  • При толщине "провода" больше $2$, "электроны" начинают двигаться хаотично.

Основные элементы

Большое количество примеров приведено в Mirek's Cellebration[17] и Zillions of Games[18], WireWorld[19]. С помощью элементов Wireworld также был построен[20] компьютер.
В данной статье приведены лишь основные простейшие элементы.

Тактовый генератор

Данный элемент используется для получения электронов, так как при каждом прохождении разветвления электроном, движущимся по петле генератора, образуется новый электрон. Частота появления электронов регулируется длиной петли.

  • Тактовый генератор

Диод

Данный элемент действует точно так же, как одноименный элемент[21] электрической цепи.

  • Диод

Логические элементы OR, XOR и NAND

Данный элемент действует точно так же, как и одноименные логические элементы[22][23][24].

  • OR

  • XOR

  • NAND

Самовоспроизводящиеся клеточные автоматы

В ходе работы над математическими и логическими проблемами самовоспроизведения, Дж. фон Нейман поставил пять основных вопросов, которые подробно описаны в книге "Физика процессов эволюции"[25]:
«

  1. Логическая универсальность.
    1. При каких условиях определенный класс автоматов логически универсален?
    2. Существует ли логически универсальный автомат?
  2. Конструируемость.
    1. Может ли один автомат быть построен другим автоматом?
    2. Какой класс автоматов может быть построен каким-то автоматом?
  3. Конструктивная универсальность.
    1. Существует ли конструктивно универсальный автомат? (т. е. автомат, способный построить любой автомат)
  4. Самовоспроизведение.
    1. Существует ли самовоспроизводящийся автомат?
    2. Существует ли автомат, который, помимо самовоспроизведения, может решать и другие задачи?
  5. Эволюция.
    1. Может ли при конструировании автомата автоматом происходить усложнение типа автомата?
    2. Может ли такая эволюция происходить в направлении от менее эффективного к более эффективному автомату? (при надлежащем определении понятия эффективности)
».

В то время, как Тьюринг доказал, что машина Тьюринга является логически универсальной, Дж. фон Нейман построил автомат[26]. Одна из таких моделей будет описана далее.

Автомат фон Неймана

Определение:
Автомат фон Неймана (клеточная модель самовоспроизведения[27]) — объект, представляющий собой поле, в каждой клетке которого находится конечный автомат с 29 состояниями.


Состояния и правила переходов

Автомат фон Неймана имеет [math]N = 29[/math] различных состояний:

  1. Транзитивные состояния (импульсы) $T_{u\alpha\varepsilon}$. Определяются:
    1. Направлением движения.
    2. Статусом (покой/возбуждение, обычное/специальное);
  2. Конфлюэнтные состояния [math]C_{\varepsilon{\varepsilon}'}[/math]. Определяются:
    1. Статусом (покой/возбуждение);
    2. Статусом на следующем такте (покой/возбуждение);
  3. Основное состояние [math]U[/math] (невозбужденное);
  4. Чувствительные (сенситивные) состояния [math]S_{\Sigma}[/math].


TODO: ADD SCHEME
Переход из $U$ в $S$ осуществляется путем возбуждения, после которого автомат проходит ряд сенситивных состояний, в конечном счете, переходя в состояние $C$ или $T$. Оба конечных состояния могут попеременно находиться в возбужденной и невозбужденной форме, оставаться неизменными или переходить снова в $U$.

Более подробно состояния и правила перехода данного автомата описаны в §5.3 книги "Физика процессов эволюции"[25].

Принцип работы

TODO: ADD PICS
Начальная конфигурация описывается конечным набором клеток, находящихся в возбудимом или чувствительном состоянии. Правила данного автомата устроены таким образом, что через некоторое количество шагов на поле появляется копия начальной конфигурации в области, отличающейся от той, в которой начальная конфигурация была задана.

Автомат Лэнгтона

Примером более простого самовоспроизводящегося клеточного автомата является автомат Лэнгтона[26].

Также интерес представляет Муравей Лэнгтона[28], разработанный в 1986 году Крисом Лэнгтоном и являющимся, по сути, двумерной машиной Тьюринга с 2 символами и 4 состояниями[29].

Определение:
Автомат Лэнгтона — двумерный клеточный самовоспроизводящийся автомат, представляющий собой сигнальную ленту, заключенную между двумя стенками.
В автомате Лэнгтона клетка может находиться в одном из восьми возможных состояний. Состояние клетки в следующий момент времени определяется состоянием в текущий момент состоянием четырех соседей.

Сигнальная лента несет информацию, необходимую для создания копии автомата.

Состояния

Сигнальные состояния

Состояния $3-7$ относят к классу сигнальных:

  • $3$ используется при повороте;
  • $5$ и $6$ используются для самовоспроизведения.

Служебные состояния

Состояния $0-2$ относят к классу служебных:

  • $0$, идущее вслед за сигнальным задает направление распространения сигнала;
  • $1$ является «несущей лентой» сигнала;
  • Из клеток в состоянии $2$ строятся «стенки» автомата.

Принцип работы

TODO: ADD PICTURES

  • Увеличение длины ленты на $1$ достигается путем передачи на ее конец сигнала $70$;
  • Поворот ленты влево достигается путем передачи на ее конец сигнала $40$;
  • Воспроизведение исходной конфигурации происходит через $151$ такт времени после запуска автомата.

Тюрьмиты

Определение:
Тьюрмит — это движущаяся по плоскости, размеченной клетками, машина Тьюринга, которая хранит свое внутреннее состояние, и, в зависимости от него и от цвета клетки, на которой она стоит, изменяет свое состояние, перекрашивает клетку в другой цвет и делает поворот влево или вправо.


Каждая строка программы записывается в следующем виде: 

<текущее состояние> <цвет клетки под тьюрмитом> <новый цвет клетки> <смена направления> <новое состояние>


TODO: ADD PICTURES
Тьюрмиты можно программировать для решения достаточно сложных задач: например, один тьюрмит может анализировать размеченную поверхность и оставлять на ней пометки для другого, который будет вносить в нее изменения. При помощи всего лишь одного тьюрмита можно реализовать[26] клеточный автомат «Жизнь»: тьюрмит обегает колонию и в соответствии с заданными правилами рисует следующее поколение.

См.также

Литература

  1. ↑ Список заданий по ДМ 2к 2020 весна. URL: http://neerc.ifmo.ru/wiki/index.php?title=%D0%A1%D0%BF%D0%B8%D1%81%D0%BE%D0%BA_%D0%B7%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B9_%D0%BF%D0%BE_%D0%94%D0%9C_2%D0%BA_2020_%D0%B2%D0%B5%D1%81%D0%BD%D0%B0
  2. ↑ Окрестность Мура. URL: https://ru.wikipedia.org/wiki/%D0%9E%D0%BA%D1%80%D0%B5%D1%81%D1%82%D0%BD%D0%BE%D1%81%D1%82%D1%8C_%D0%9C%D1%83%D1%80%D0%B0
  3. ↑ Weisstein, Eric W. Moore Neighborhood. URL: https://mathworld.wolfram.com/MooreNeighborhood.html
  4. ↑ Окрестность фон Неймана. URL: https://ru.wikipedia.org/wiki/%D0%9E%D0%BA%D1%80%D0%B5%D1%81%D1%82%D0%BD%D0%BE%D1%81%D1%82%D1%8C_%D1%84%D0%BE%D0%BD_%D0%9D%D0%B5%D0%B9%D0%BC%D0%B0%D0%BD%D0%B0
  5. ↑ Сад Эдема (конфигурация клеточного автомата). URL: https://ru.wikipedia.org/wiki/%D0%A1%D0%B0%D0%B4_%D0%AD%D0%B4%D0%B5%D0%BC%D0%B0_(%D0%BA%D0%BE%D0%BD%D1%84%D0%B8%D0%B3%D1%83%D1%80%D0%B0%D1%86%D0%B8%D1%8F_%D0%BA%D0%BB%D0%B5%D1%82%D0%BE%D1%87%D0%BD%D0%BE%D0%B3%D0%BE_%D0%B0%D0%B2%D1%82%D0%BE%D0%BC%D0%B0%D1%82%D0%B0)
  6. ↑ Moore, E. F. (1962), Machine models of self-reproduction, Proc. Symp. Applied Mathematics Т. 14: 17–33
  7. ↑ Wolfram, Stephen, A New Kind of Science. Wolfram Media, Inc., May 14, 2002. ISBN 1-57955-008-8
  8. ↑ 8,0 8,1 8,2 Скаков П.С. Классификация поведения одномерных клеточных автоматов. СПб., 2007 — URL: http://is.ifmo.ru/diploma-theses/_skakov_master.pdf
  9. ↑ Eppstein D. Classification of Cellular Automata. http://www.ics.uci.edu/~eppstein/ca/wolfram.html
  10. ↑ Wolfram, Stephen (July 1983). "Statistical Mechanics of Cellular Automata". Reviews of Modern Physics. 55: 601–644
  11. ↑ Игра "Жизнь". URL: https://ru.wikipedia.org/wiki/%D0%98%D0%B3%D1%80%D0%B0_%C2%AB%D0%96%D0%B8%D0%B7%D0%BD%D1%8C%C2%BB
  12. ↑ «Словарь Жизни». URL:http://beluch.ru/life/lifelex/lexr_o.htm
  13. ↑ Eric Weisstein. Still Life
  14. ↑ Gardner, M. (1983). "The Game of Life, Part III". Wheels, Life and Other Mathematical Amusements: 246
  15. ↑ Breeder – from Eric Weisstein's Treasure Trove of Life
  16. ↑ Трофимов Д., Наумов Л. Реализация клеточного автомата WireWorld с помощью инструментального средства CAME&L и его зональная оптимизация, 2007. URL: http://is.ifmo.ru/works/wireworld/
  17. ↑ "Mirek's Cellebration". URL:http://mirekw.com/ca/index.html
  18. ↑ "Zillions of Games". URL:http://zillionsofgames.com
  19. ↑ "WireWorld". URL:http://karl.kiwi.gen.nz/CA-Wireworld.html.
  20. ↑ "The Wireworld computer". URL:http://www.quinapalus.com/wi-index.html
  21. ↑ Диод. URL: https://ru.wikipedia.org/wiki/Диод
  22. ↑ Дизъюнкция. URL: https://ru.wikipedia.org/wiki/Дизъюнкция
  23. ↑ Исключающее «или». URL: https://ru.wikipedia.org/wiki/Исключающее_«или»
  24. ↑ NAND (логический элемент). URL: https://ru.wikipedia.org/wiki/Штрих_Шеффера
  25. ↑ 25,0 25,1 Эбелинг Вернер, Энгель Андреас, Файстель Райнер. Физика процессов эволюции. Пер. с нем. Ю. А. Данилова. — М.: Эдиториал УРСС, 2001. - 328 с.
  26. ↑ 26,0 26,1 26,2 Г. Г. Малинецкий, Н. А. Митин, С. А. Науменко, “Нанобиология и синергетика. Проблемы и идеи (Часть 2)”, Препринты ИПМ им. М. В. Келдыша, 2005, 081. URL: http://spkurdyumov.ru/uploads/2013/09/miittin.pdf
  27. ↑ Нейман Дж. фон. Теория самовоспроизводящихся автоматов. М.: Мир, 1971
  28. ↑ Langton, Chris G. (1986). "Studying artificial life with cellular automata", 120–149
  29. ↑ Mária Bieliková, Gerhard Friedrich, Georg Gottlob. SOFSEM 2012: Theory and Practice of Computer Science: 38th Conference on Current Trends in Theory and Practice of Computer Science, Špindlerův Mlýn, Czech Republic, January 21-27, 2012, Proceedings. — Springer, 2012. — P. 394. — ISBN 978-3-642-27660-6.
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Модели_клеточных_автоматов&oldid=74790»