Обнаружение и исправление ошибок кодирования
Пусть — булевое множество. Рассмотрим и расстояние Хемминга . Пусть — разделяемый код постоянной длины. Обозначим .
Коды, обнаруживающие и исправляющие ошибки
| Определение: |
| Код обнаруживает ошибок, если . |
| Определение: |
| Код исправляет ошибок, если . |
| Утверждение: |
Код, исправляющий ошибок, обнаруживает ошибок. |
Булев шар
| Определение: |
| Булев шар — подмножество вида . называется его центром, — радиусом. Булев шар с центром и радиусом обознчается . |
| Определение: |
| Обьёмом шара в называется величина . Обьём шара радиуса в обозначается . |
| Утверждение: |
Обьём шара не зависит от его центра. |
|
Заметим, что шар всегда можно получить из другого шара с помощью "параллельного переноса" на вектор (здесь обозначает побитовый ), т.е. . Покажем это. Необходимо доказать, что при и . . |
Можно сформулировать свойство кодов, исправляющих ошибок, в терминах булевых шаров.
| Лемма: |
Пусть — код, исправляющий ошибок.
Тогда для любых неравных выполнено . |
| Доказательство: |
|
Т.к код исправляет ошибок, по определению . Допустим, такие, что и , т.е существует , такой что и . Тогда по неравенству треугольника . Это противоречит тому, что . |
Определение и устранение ошибок в общем случае
Пусть — исходный алфавит, — кодирование,
— расстояние Хэмминга между двумя кодами.
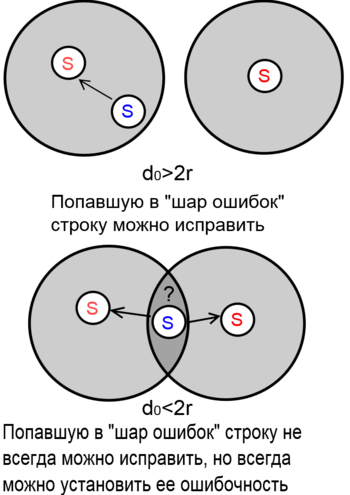
Код, может исправлять и обнаруживать ошибок. Действительно, при любом натуральном количестве допустимых ошибок любоое кодовое слово образует вокруг себя проколотый шар таких строк , что . Если этот шар не содержит других кодов (что выполняется при ) , то можно утверждать, что если в него попадает строка, то она ошибочна. Если шары всех кодов не пересекаются (что выполняется при ), то попавшую в шар строку можно считать ошибочной и исправить на центр шара — строку .
Граница Хэмминга, граница Гильберта
| Теорема (Граница Хэмминга): |
Пусть — код для -символьного алфавита, исправляющий ошибок.
Тогда выполнено неравенство . |
| Доказательство: |
|
Это прямое следствие предыдущей леммы. Всего есть попарно непересекающихся шаров. Их суммарный обьём равен , и он не может превосходить общее число возможных веткоров . |
Граница Хэмминга даёт верхнюю оценку на скорость передачи сообщений в канале с ошибками. Прологарифмировав неравенство, получим . Здесь это плотность кодирования, количество информации в одном символе алфавита на размер кода. Таким образом, при кодировании с защитой от ошибок падает скорость передачи.
Аналогично составляется оценка в другую сторону.
| Теорема (Граница Гильберта): |
Если выполнено неравенство , то существует код для -символьного алфавита , исправляющий ошибок. |
Примером кода для случая является код Хэмминга.