QpmtnCmax
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
| Задача: |
| Дано станков с разной скоростью выполнения работ, работающих параллельно, и работ. Работа может быть прервана в любой момент и продолжена позже на любой машине. Необходимо минимизировать время выполнения всех работ. |
Алгоритм построения расписания
Описание алгоритма
Перед выполнением алгоритма, упорядочим все работы по убыванию их времени выполнения:, а все машины в порядке убывания скоростей: . Введем следующие обозначения:
- , — сумма первых работ
- , — сумма скоростей первых станков
Необходимое условие для выполнения всех работ в интервале :
или
Кроме того, должно выполняться условие для всех , так как это нижняя оценка времени выполнения работ . Исходя из этого получаем нижнюю границу :
Перейдем к описанию алгоритма. Будем назвать -ом работы невыполненную часть работы в момент времени .
Далее построим расписание, которое достигает нашей оценки , с помощью -алгоритма.
Псевдокод
Функция принимает на вход два массива — массив с объемами работ и массив скоростей обработки станков, и возвращает вектор четвёрок, где первый элемент является номером станка, второй — номером работы, а два оставшихся время начала и окончания обработки этой работы на этом станке.
function level(p : int[n], s : int[m]) : vector<int, int, int, int>
vector<int, int, int, int> ans
int t = 0
int k = n // количество еще не выполненных работ
sort(p) // сортируем время обработки работ по убыванию
sort(s) // сортируем станки по убыванию скоростей
while k > 0
int[] to = assign(p, k, m) // получаем распределение работ по станкам
Найдем минимальное dt1 отличное от нуля такое, что (p[i] - s[to[i]] * dt1) = 0
Найдем минимальное dt2 такое, что p[i] > p[j] и (p[i] - s[to[i]] * dt2 = p[j] - s[to[j]] * dt2) // то есть такое минимальное время, через которое,
// оставшийся объем каких-нибудь двух работ сравняется
int dt = min(dt1, dt2)
for j = 0 to n - 1
if p[j] > 0
if to[j] -1 // рассматриваем работы которые обрабатываются в данном распределении
ans.push(to[j], j, t, t + dt)
p[j] -= s[to[i]] * dt
if p[j] == 0
k--
t += dt // поиск следующего момента времени, в который нужно будет перераспределить машины/работы
return ans
Функция принимает на вход массив с объемами работ и возвращает массив с распределением работ.
function assign(p : int[n], k : int, m : int) : int[]
int[n] to // j работа обрабатывается на to[j] станке
fill(to, -1)
set<int> s // множество уже распределенных работ
int i = 0
while i < m and i < k
Находим первый j такой что p[j] максимальный и s не содержит j
s.add(j)
m[j] = i++
return to
Асимптотика
-алгоритм вызывает функцию в самом худшем случае раз. Функция выполняется за . Итоговое время работы .
Доказательство корректности алгоритма
| Теорема: |
Расписание, построенное данным алгоритмом, является корректным и оптимальным. |
| Доказательство: |
|
Так как нижняя граница :
то достаточно показать, что составленное расписание достигает этой оценки. Будем считать, что в начале алгоритма все работы упорядочены, как было сказано ранее: . Это утверждение не меняется на протяжении всего выполнения алгоритма, для любого момента времени. Получаем: . Докажем что алгоритм составляет расписание в соответствии с этим свойством. Чтобы доказать этот факт, будем считать что в любой момент времени нет простоев машин, когда есть хотя бы одна невыполненная работа. Получаем: или Таким образом необходимая оценка достигается нашим алгоритмом. Допустим хотя бы одна машина простаивает, в момент когда есть невыполненные работы, получим следующее неравенство для времен окончания работ (обозначим далее как ) на станках , пронумерованных по убыванию скоростей:
Докажем написанное выше неравенство: Предположим, что для некоторого . Тогда последней работы, выполнявшейся на станке в момент времени (где достаточно мал) меньше, чем последней работы на станке . Пришли к противоречию, так как при распределении, работы с наибольшим выставлялись на самые быстрые станки. Пусть = ,где . Чтобы работы завершились в момент времени , необходимо начать их в момент времени 0, поскольку если это не выполняется, то у нас найдется работа , которая начинается позже и заканчивается в . Это означает, что в момент времени начинаются как минимум работ. Пусть первые работ стартовали вместе на всех машинах. Мы получаем , из чего следует, что для любого , удовлетворяющего условию . Таким образом, до момента времени нет простаивающих машин. Пришли к противоречию. Получаем . |
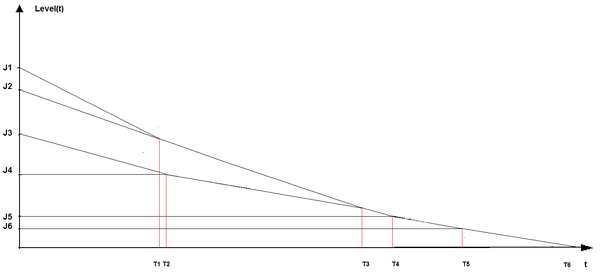
Пример
Пусть у нас есть работ и станка. Покажем работу алгоритма для данного случая.
В начальный момент времени начинаем обрабатывать работы с наибольшим временем выполнения , и на станках , и соответственно. В момент времени -ой работы и -ой работы совпадает. С этого момента начинаем обрабатывать работы и синхронно на станках: и . В момент времени работа опускается до уровня работы .Работы и выполняем одновременно на одном станке . В момент времени начинаем выполнять первые четыре работы на всех станках одновременно, далее просто добавятся работы и , и все работы закончатся одновременно.
См. также
Источники информации
- Peter Brucker. «Scheduling Algorithms» — «Springer», 2006 г. — 124 — 129 стр. — ISBN 978-3-540-69515-8