Факторизация графов
| Определение: |
| Фактором (англ. factor) графа называется остовный подграф графа , имеющий хотя бы одно ребро. |
| Определение: |
| Граф — сумма факторов , если графы не имеют попарно общих рёбер, а является их объединением. Такое разложение называется факторизацией (англ. factorization) графа . |
| Определение: |
| -фактор — регулярный остовный подграф степени . Если граф представляет собой сумму -факторов, то их объединение называется -факторизацией, а сам граф назыается -факторизуемым. |
| Определение: |
| Пусть задана функция , такая что . Тогда остовный подграф в котором степень каждой вершины равна называется -фактором. |
Задача о поиске произвольного -фактора
Сведем задачу о поиске -фактора к задаче о поиске наибольшего паросочетания.
Пусть дан граф и функция . Построим граф следующим образом.
- Для каждого ребра добавим в граф по одной новой вершине в множества и , и соединим их ребром . В результате каждой вершине будет соответствовать множество такое что ; Каждому ребру будет соответствовать ребро , причем ни для каких двух ребер из концы соответствующих им ребер в не пересекаются.
- Для каждой вершины добавим в новые вершин, образующие множество . Каждую вершину из свяжем ребром с каждой вершиной из . В результате для каждой вершины Множество образует полный двудольный граф.
| Теорема: |
Граф имеет -фактор тогда и только тогда, когда соответствующий графу и функции граф имеет совершенное паросочетание. |
| Доказательство: |
|
Пусть граф имеет -фактор . Построим паросочетание для графа следующим образом:
В результате каждая вершина в покрыта , следовательно является совершенным паросочетанием. Пусть имеет совершенное паросочетание . Для каждой вершины является независимым множеством и полностью покрыто , следовательно множество покрыто ребрами, концы которых лежат в , а значит каждая вершина из покрыта ребром, второй конец которого принадлежит , причем . Поэтому если мы добавим в все ребра соответствующие ребрам из покрывающим , то есть все ребра из концы которых лежат в множествах , то степень каждой вершины будет равна , а значит будет являться -фактором. |
Из доказательства напрямую следует, что для нахождения -фактора графа достаточно найти совершенное паросочетание в графе . Т.к. в общем случае не является двудольным, для решения этой задачи можно воспользваться Алгоритмом Эдмондса для поиска наибольшего паросочетания работающим за время . Построение графа можно выполнить за время . Поэтому итоговая асимптотика —
1-факторизация
| Теорема: |
Полный граф -факторизуем. |
| Доказательство: |
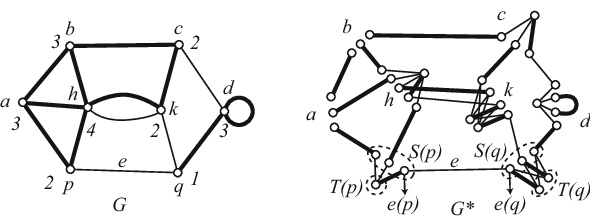
| Нам нужно только указать разбиение множества рёбер графа на -фактора. Для этого обозначим вершины графа через и определим множества рёбер , , где каждый из индексов и является одним из чисел ; здесь сумма и разность берутся по модулю . Легко видеть, что набор даёт необходимое разбиение множества , а сумма подграфов , порождённых множествами , является -факторизацией графа . |
2-факторизация
| Утверждение: |
Если граф -факторизуем, то каждый его фактор должен быть объединением непересекающихся (по вершинам) циклов. |
| Начнём обход -фактора с какой-то вершины. Пойдём по одному из её рёбер и попадаем в смежную ей вершину. Далее идём по рёбрам, по которым мы ещё не ходили. Мы входим в вершину по одному ребру и выходим по другому, так как степень каждой вершины равна , пока не вернёмся в первую вершину. Это цикл, так как в каждой вершине мы были только один раз. Если есть вершины, которые мы не посетили, то снова начинаем обход с любой из таких вершин. В вершины прежних циклов попасть нельзя, так как мы уже проходили по рёбрам этих вершин. Значит, циклы не пересекаются по вершинам. |
| Теорема (J. Petersen, 1981, О наличии -фактора в регулярном графе чётной степени.): |
Пусть — регулярный граф чётной степени. Тогда в есть -фактор. |
| Доказательство: |
|
Пусть — -регулярный граф, пусть связен. Согласно критерию эйлеровости граф имеет эйлеров цикл , где . Будем строить граф следующим образом: разделим каждую вершину графа на две, назовём их и . Заменим каждое ребро в эйлеровом обходе на ребро
Объединим вершины и обратно в вершину . Так как в графе каждой вершине было инцидентно ребро, то после объединения в графе каждой вершине будет инцидентно ребра. Если несвязен, то аналогичные рассуждения можно провести для каждой его компоненты связности, и, таким образом, найти -фактор в каждой его компоненте связности. Тогда каждой вершине каждой его компоненты связности будет инцидентно ребра, значит, каждой вершине будет инцидентно ребра, значит, в существует -фактор. |
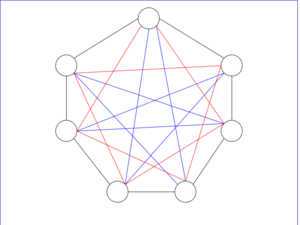
Заметим, что если -фактор связен, то он является гамильтоновым циклом.
| Теорема: |
Граф можно представить в виде суммы гамильтоновых циклов. |
| Доказательство: |
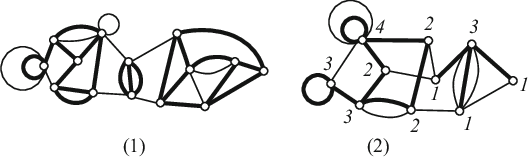
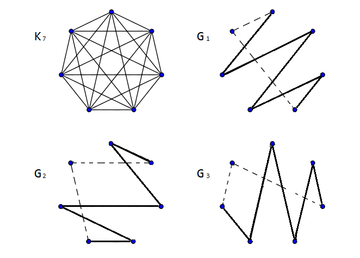 -факторизация графа . Рёбра, отмеченные пунктиром, не пересекают другие рёбра при правильной укладке графа. |
Замечания
- Факторизация графов используется как один из способов построения покрывающих наборов, используемых при создании тестов для программ с большим количеством параметров.
- -факторизация -регулярного графа является рёберной -раскраской графа.
См. также
Источники информации
- Харари Фрэнк Теория графов Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Wikipedia — Graph factorization
- Factors and Factorizations of Graphs: Proof Techniques in Factor Theory / Jin Akiyama, Mikio Kano. — Springer Science & Business Media, 2011. ISBN 3642219187, 9783642219184.